\(h_{1}, h_{2}, h_{3}, w_{1}, w_{2}, w_{3}\) を以下のように定義された値とします。

• \(h_{1} = A - 1\)
• \(h_{2} = B - A + 1\)
• \(h_{3} = H - B\)
• \(w_{1} = C - 1\)
• \(w_{2} = D - C + 1\)
• \(w_{3} = W - D\)

マスを下図のように \(A, B, C, D, E, F, G, H\) の \(8\) 領域に分割し、それぞれのマスに置かれた照明の数を \(a, b, c, d, e, f, g, h\) とします。(\(A, B, C, D\) はこれ以降、領域の名前を指すことに注意してください。)

全ての白マスを照らす条件

領域 \(A\) は領域 \(A, E, F\) に置かれた照明によってのみ照らされます。よって、領域 \(A\) のすべてのマスを照らすためには、以下のいずれかが満たされていなければなりません。

• \(a + e + f = h_{1}\)
• \(a + e + f \neq h_{1}\) かつ \(a = w_{2}\)

\(a+e+f = h_1\) のとき

領域 \(A, E, F\) のすべてのマスが照らされます。

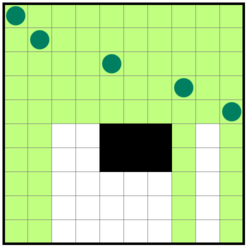
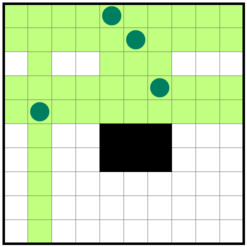
\(a=w_2\) (かつ \(a+e+f \neq h_1\))のとき

領域 \(A\) のすべてのマスが照らされ、 \(E, F\) には照らさないマスが残ります。ここで残されたマスについては他の領域に置かれた照明によって、縦から照らされていなければならないことに注意します。

同様に領域 \(B\) の全ての白マスを照らすことを考えると、以下のいずれかが成り立つ必要があります。

• \(b + e + g = w_{1}\)
• \(b + e + g \neq w_{1}\) かつ \(b = h_{2}\)

次に領域 \(E\) の全ての白マスを照らすことを考えます。

上から \(h_{1}\) 行で照明が置かれていない行があり、かつ、左から \(w_{1}\) 列で照明が置かれていない列があるとします。 このとき、それらの行と列にある白マスはどの照明にも照らされていません。よって、条件を満たしません。 このことを踏まえると、領域 \(E\) の全ての白マスを照らすためには、以下のいずれかが成り立っている必要があります。

• \(a + e + f = h_{1}\)
• \(b + e + g = w_{1}\)

領域 \(F, G, H\) に対しても同様に考えると、領域 \(E, F, G, H\) の白マスを全て照らすには、以下のいずれかが成り立っている必要があります。

• \(a + e + f = h_{1}\) かつ \(d + g + h = h_{3}\)
• \(b + e + g = w_{1}\) かつ \(d + f + h = w_{3}\)

これらのことを踏まえてこの問題を解くことを考えます。

数え上げ

領域 \(A, B, C, D\) を照らす条件を満たすように照明の配置の一部を決め、その後領域 \(E, F, G, H\) を照らす条件を満たすように照明の配置の残りを決めることを考えます。

領域 \(A\) のすべてのマスを照らすためには、以下のいずれかが満たされていなければなりません。

• \(a + e + f = h_{1}\)
• \(a + e + f \neq h_{1}\) かつ \(a = w_{2}\)

\(a + e + f = h_{1}\) かつ \(e + f = i\) が成り立つように領域 \(A\) に照明を置く場合の数 \(\binom{w_{2}}{h_{1} - i}\frac{h_{1}!}{i!}\) を \(X_{0}[i]\) とします。

また、\(a + e + f\neq h_{1}\)、\(a=w_{2}\)かつ \(e + f = i\) としたときの「領域 \(A\) の照明の配置」と「領域 \(E, F\) の中で照明を置かれている行の集合」の組の場合の数 \(\binom{h_1 - w_2}{i}\cdot\frac{h1!}{(h1 - w2)!}\) を求め、 これを \(X_{1}[i]\) とします。

上記のものを領域 \(C, G, H\) でも考えたものを \(Y_{0}[i], Y_{1}[i]\) とし、\(P_{0}[i], P_{1}[i]\) をそれぞれ以下のように定義します。

• \(\displaystyle P_{0}[i] = \sum_{j + k = i} X_{0}[j]\cdot Y_{0}[k]\)
• \(\displaystyle P_{1}[i] = \sum_{j + k = i} X_{0}[j]\cdot Y_{1}[k] + X_{1}[j]\cdot Y_{0}[k] + X_{1}[j]\cdot Y_{1}[k]\)

これらの \(P_{0}[i], P_{1}[i]\) は以下の場合の数に対応しています。

• \(P_{0}[i], P_{1}[i]\) : 領域 \(A, D\) の照明が置かれている白マスと、領域 \(E, F, G, H\) の照明が置かれる行の集合が固定されていて、かつ行の集合の個数は \(i\) である。
• \(P_{0}[i]\) : \(a + e + f = h_{1}\) かつ \(d + g + h = h_{3}\) が成り立つ
• \(P_{1}[i]\) : \(a + e + f \neq h_{1}\) または \(d + g + h \neq h_{3}\) が成り立つ。

同様に列でも考えたものをそれぞれ \(Q_{0}[i], Q_{1}[i]\) とします。具体的には以下の場合の数とします。

• \(Q_{0}[i], Q_{1}[i]\) : 領域 \(B, C\) の照明が置かれている白マスと、領域 \(E, F, G, H\) に照明が置かれる列の集合が固定されていて、かつ列の集合の個数は \(i\) である。
• \(Q_{0}[i]\) : \(b + e + g = w_{1}\) かつ \(c + f + h = w_{3}\) が成り立つ
• \(Q_{1}[i]\) : \(b + e + g \neq h_{1}\) または \(c + f + h \neq w_{3}\) が成り立つ。

領域 \(E, F, G, H\) に照明を計 \(i\) 個おくことを考えます。置く行と列の集合が固定されているとき、置き方の個数は \(i!\) となります。

よって、答えは以下の式で表せます。

• \(\displaystyle \sum_{i} (P_{0}[i]\cdot Q_{0}[i] + P_{0}[i]\cdot Q_{1}[i] + P_{1}[i]\cdot Q_{0}[i])\cdot i!\)

時間計算量は \(P_{0}, P_{1}, Q_{0}, Q_{1}\) などを求める部分がボトルネックとなり、atcoder::convolution などで畳み込むことで時間計算量 \(O((H+W)\log(H+W))\) で解くことができます。