 /
/ 
Time Limit: 1 sec / Memory Limit: 976 MiB
配点:800 点
問題文
H \times W のマス目で表されるボードがあります。マス目の i \ (1 \leq i \leq H) 行目で j (1 \leq j \leq W) 列目のマスを (i, j) とします。
いくつかのマスにはコインがあります。S_{i, j} = o のとき、マス (i, j) に 1 つだけコインがあり、x のときコインがありません。
ロボットがコインのあるマスから上下左右のいずれかの方向を向いてスタートします。スタート位置と方向は E869120 君が自由に決めることができます。
その後、E869120 君は次の操作を繰り返します。
- その場にあるコインを取った後、90 度左回転または 90 度右回転し、向いている方向に 1 マス以上進んだコインのある位置までジャンプする。
スタートする位置と方向、ジャンプする位置、回転する方向をうまく決めたときに、E869120 君はすべてのコインを回収することができるでしょうか?
制約
- 2 \leq H \leq 100
- 2 \leq W \leq 100
- S_{i, j} は
oまたはxのいずれか - 最低 1 つのコインがボード上にある
部分点
この問題はいくつかの小課題に分けられ、その小課題のすべてのテストケースに正解した場合に「この小課題に正解した」とみなされます。
提出したソースコードの得点は、正解した小課題の点数の合計となります。
- (100 点):N \leq 8
- (110 点):N \leq 16
- (150 点):H = 2
- (440 点):追加の制約はない。
ただし、ここで N は「マス目上にあるコインの枚数」とします。
入力
入力は以下の形式で標準入力から与えられます。
H W
S_{1, 1}S_{1, 2}S_{1, 3}...S_{1, W}
S_{2, 1}S_{2, 2}S_{2, 3}...S_{2, W}
: : :
S_{H, 1}S_{H, 2}S_{H, 3}...S_{H, W}
出力
コインをすべて回収する方法があるならば Possible、どのような行動を取ってもコインをすべて回収できないならば Impossible と出力してください。
入力例 1
5 5 xooxx xoxxo xxoox ooxoo xoxxx
出力例 1
Possible
次のような順序でロボットを動かすと、すべてのコインを回収することができます。
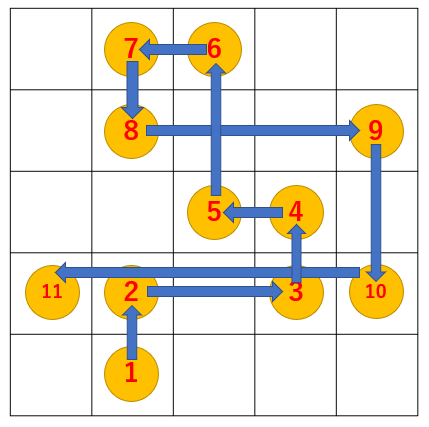
入力例 2
2 9 oxxxxoxxo oxoxxoxxo
出力例 2
Possible
次のような順序でロボットを動かすと、すべてのコインを回収することができます。

入力例 3
9 25 xxxxxxxxxxxxxxxxxxxxxxxxx xxoooxxxoooxxooooxxxoooxx xoxxxoxoxxxoxoxxxoxoxxxox xoxxxxxoxxxoxoxxxoxoxxxxx xxoooxxxoooxxooooxxoxxxxx xxxxxoxoxxxoxoxxxxxoxxxxx xoxxxoxoxxxoxoxxxxxoxxxox xxoooxxxoooxxoxxxxxxoooxx xxxxxxxxxxxxxxxxxxxxxxxxx
出力例 3
Impossible
どのようなロボットの動かし方をしても、すべてのコインを回収することができません。
入力例 4
6 6 oxxxxo xoooxx xoooox xoooox xxooxx oxxxxo
出力例 4
Impossible
この場合も、どのようなロボットの動かし方をしても、すべてのコインを回収することができません。
Max Score:800 points
Problem Statement
There is a rectangular board with H \times W cells. The cell of i-th row and j-th column is denoted by (i, j).
There are coins in some cells. If S_{i, j} = o, there is one coin in (i, j). Otherwise, if S_{i, j} = x, there is no coins in (i, j).
E869120 will place a robot in cell with coin, and he will set the initial direction, choosing from up / down / left / right. Then, the robot will repeat the following actions.
- Collect the coins in the cell of robot. Then, rotate 90 degrees left or right. After that, jump to any cell with coin that advances at least 1 cells in the direction robot faces.
E869120's objective is to collect all coins in the board. Determine if there's a way to fulfill the objective when E869120 can decide initial cell/direction of robot, and the direction of rotation and destination of jumps for each action.
Constraints
- 2 \leq H \leq 100
- 2 \leq W \leq 100
- S_{i, j} is either
oorx. - There is at least 1 coin on the board.
Subtasks / Scoring
This problem is separated several two subtasks, and you will get score of the subtask if your program prints the correct answer for all testcases for the subtask prepared.
The score for a program is the sum of score of subtasks of correct answer.
- (100 points):N \leq 8
- (110 points):N \leq 16
- (150 points):H = 2
- (440 points):No additional constraints.
When we let N the number of coins on the board.
Input
The input will be given from standard input, in the following format.
H W
S_{1, 1}S_{1, 2}S_{1, 3}...S_{1, W}
S_{2, 1}S_{2, 2}S_{2, 3}...S_{2, W}
: : :
S_{H, 1}S_{H, 2}S_{H, 3}...S_{H, W}
Output
Print Possible if there is a way to collect all coins; otherwise, print Impossible.
Sample Input 1
5 5 xooxx xoxxo xxoox ooxoo xoxxx
Sample Output 1
Possible
He can fulfill the objective by moving like the following picture.

Sample Input 2
2 9 oxxxxoxxo oxoxxoxxo
Sample Output 2
Possible
He can fulfill the objective by moving like the following picture.

Sample Input 3
9 25 xxxxxxxxxxxxxxxxxxxxxxxxx xxoooxxxoooxxooooxxxoooxx xoxxxoxoxxxoxoxxxoxoxxxox xoxxxxxoxxxoxoxxxoxoxxxxx xxoooxxxoooxxooooxxoxxxxx xxxxxoxoxxxoxoxxxxxoxxxxx xoxxxoxoxxxoxoxxxxxoxxxox xxoooxxxoooxxoxxxxxxoooxx xxxxxxxxxxxxxxxxxxxxxxxxx
Sample Output 3
Impossible
He cannot collect all coins no matter how he commanded the robot.
Sample Input 4
6 6 oxxxxo xoooxx xoooox xoooox xxooxx oxxxxo
Sample Output 4
Impossible
He cannot collect all coins no matter how he commanded the robot, also in this case...