B - Falling Stone Game
Editorial
 /
/ 
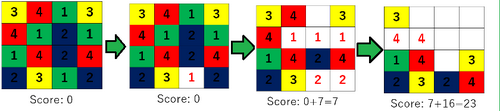 よって, $7+16=23$ 点となる。
よって, $7+16=23$ 点となる。
また, 場所 $(4,3)$ を消すのが最適である。
問題作成者:E869120
 /
/ 
Time Limit: 1 sec / Memory Limit: 256 MiB
配点: $300$ 点
この試験の内容は、以下のようなものであります。
square1001氏を助けるために、最大の点数を出力しなさい。
問題文
square1001氏は、パソコン部に入るために試験を受けました。この試験の内容は、以下のようなものであります。
- $H \times W$ の盤面が与えられる。
- その盤面の各マスは、 $1 \sim 9$ の数字が書かれている。また、1行目が一番上である。
- あなたは、セルのうち1つのマスを消すことができる。消した上のマスは落ちてくる。
- 1:$K$ 個以上の水平に隣り合うセルに同じ数字を彫った石があれば,これらの石は消滅する.こうした石群の消滅はすべて同時に起きる。
- 2:石が消滅したセルの上方のセルに石があれば,空きを埋めるように石が落下する。
- 3:すべての石の落下完了後に,消滅の条件を満たすようになった石群があれば,ステップ1に戻って繰り返す。
- 4:スコアは, $2^i \times \left(i \text{回目の消滅で消えた数字の値の和}\right)$ の合計である。ただし、最初の消滅を0回目とする。
square1001氏を助けるために、最大の点数を出力しなさい。
入力
入力は以下の形式で標準入力から与えられる。$H \ W \ K$ $c_{1, 1} \ c_{1, 2} \ \cdots \ c_{1, W}$ $c_{2, 1} \ c_{2, 2} \ \cdots \ c_{2, W}$ $\vdots \ \ \ \ \ \ \ \ \ \ \vdots \ \ \ \ \ \ \ \ \ \ \vdots$ $c_{H, 1} \ c_{H, 2} \ \cdots \ c_{H, W}$
- 1行目に, 盤面の縦、横の大きさ$H$, $W$と、何個横に並ぶと消滅するかを表す数 $K$ が与えられる。
- 2行目から, $H$行にわたって盤面の状況が与えられる。
1~9はそれぞれの数字があることを示す。
出力
出力は以下の形式で標準出力に従うこと。- 最大の点数を1行に出力しなさい。
制約
- $2 \le H, W \le 30$
- 点数は $1,000,000,000$ 点を超えない
- 最初の盤面では, すべての横に隣り合うマス同士は同じ数が書かれていることはない。
小課題
小課題1 [ $120$ 点 ]- $H, W \le 10$
- $W=K$
- 追加の制約はない。
入力例1
4 4 2 3413 4121 1424 2312
出力例1
23場所 $(4, 3)$ を押すと以下のようになります。

また, 場所 $(4,3)$ を消すのが最適である。
入力例2
4 4 2 1212 2121 1212 2121
出力例2
54この入力例は小課題1の制約を満たさない。
入力例3
7 7 2 8989898 9898989 8989898 9898989 8989898 9898989 8989898
出力例3
2520この入力例は小課題1の制約を満たさない。
入力例4
17 17 2 12345678912345678 23456789123456789 34567891234567891 45678912345678912 56789123456789123 67891234567891234 78912345678912345 89123456789123456 91234567891234567 12345678912345678 23456789123456789 34567891234567891 45678912345678912 56789123456789123 67891234567891234 78912345678912345 89123456789123456
出力例4
2354638連鎖数が非常に大きくなることもある。