M - 分割/Divide Editorial by kyopro_friends

「数列を分割した後、もともと \(A_i\) だった要素の直後にくる要素は何か？」という割当問題を考えます。

割当にかかるコストを

  • \(A_i\) の直後に \(A_j\) \((j>i)\) を割り当てるとコスト \(|A_i-A_j|\)
  • \(A_i\) の直後に「数列の終端」を割り当てるとコスト \(C\)

とすると、この割当問題の最小コストは元の問題の答えに一致します。割当問題は二部グラフの最小重みマッチングに帰着され、最小費用流を用いて解くことができます。

割当問題における辺の張り方の詳細 問題の定式化：
$X=\{X_1,\ldots,X_N\},Y=\{Y_1,\ldots,Y_M\}$ とコスト関数 $g:X\times Y\to \mathbb{R}$ が与えられる。単射 $f:X\to Y$ であって、$\sum_{x\in X} g(x,f(x))$ が最小となるものを求めよ。
解き方：
ソースとなる頂点 $S$ と、シンクとなる頂点 $T$ 、$X,Y$ の各要素に対応する頂点を用意し、以下のように辺を張る。
  • $S$ から $X_i$ に容量$1$ コスト $0$ の辺を張る
  • $X_i$ から $Y_j$ に容量 $1$ コスト $g(X_i,Y_j)$ の辺を張る
  • $Y_i$ から $T$ に容量 $1$ コスト $0$ の辺を張る
このとき $S$ から $T$ への最大流(流量$N$)の最小費用が求めるものである。

「数列の終端」は最大 \(N\) 回選ばれるため、上述の割当問題の解法をそのまま使う場合、「数列の終端」に対応する頂点を \(N\) 個用意する必要があるように思えます。しかし、実は \(T\) への辺の容量を変えることで、頂点は \(1\) つのまま使用回数の上限を指定することができます。グラフは例えば以下のようになります。（\(\text{end}\to T\) のみ容量 \(N\)、それ以外は容量 \(1\)）

図

実装例(C++/with ACL)

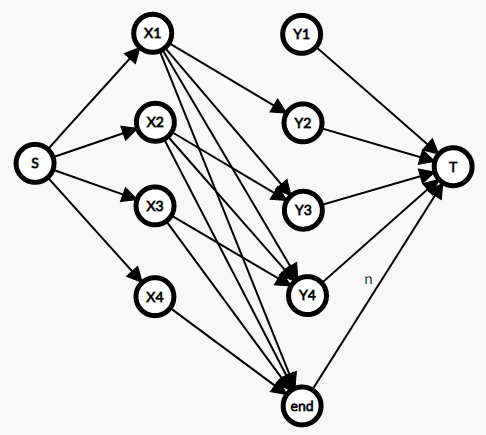
余談ですが、この解法では \(\text{end}\to T\) の辺の容量を変更することで、「高々 \(K\) 個の部分列に分解する」という問題も解くことができます。

posted:
last update: