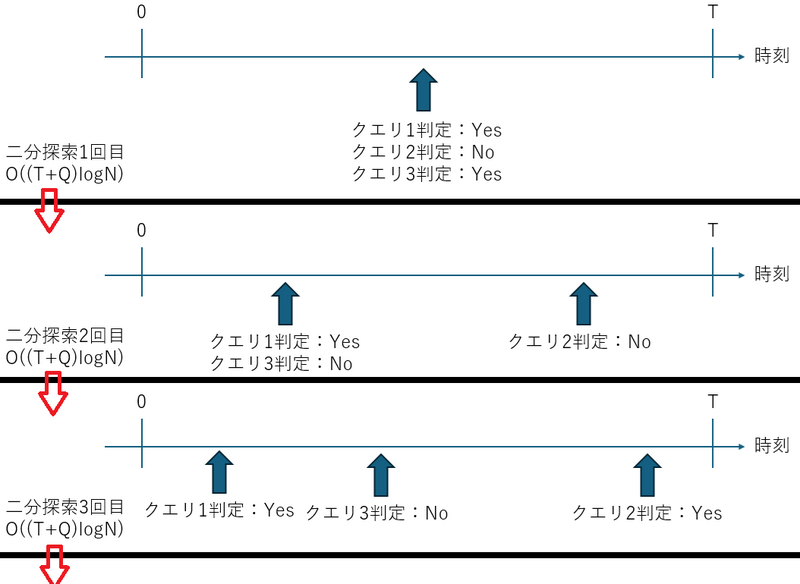
この問題は並列二分探索により解くことができます。

まずは時刻と区間和の役割を入れ替えた次の問題を考えます。

• 問題：操作は元の問題と同じ。次の形のクエリが \(Q\) 個与えられる。
  • 整数 \(l_i,r_i,t_i\) が与えられる。時刻 \(t_i\) における \(A_{l_i}+A_{l_i+1}+\dots+A_{r_i}\) の値を求める。

この問題はクエリを先読みして時刻順に並べておくことで、遅延セグメントツリーを用いて \(O((T+Q)\log N)\) で求めることができます。

元の問題についても、各クエリについて時刻で二分探索を行うこととし、二分探索の各ステップを \(Q\) 個のクエリでまとめて行うことで、全体で \(O((T+Q)\log N\log T)\) で処理することができます。

実装例(C++)

#include<bits/stdc++.h>
#include<atcoder/lazysegtree>
using namespace std;
using ll=long long;

// range add, range sum, lazy segment tree
using S=array<ll,2>;//(sum,len)
S op(S x, S y){return {x[0]+y[0], x[1]+y[1]};}
S e(){return{0,0};}
using F=ll;
S mapping(F t, S x){ return{x[0]+x[1]*t,x[1]};}
F composition(F t, F s){return t+s;}
F id(){return 0;}

int main(){
	int n,t,q;
	cin >> n >> t >> q;

	vector<array<ll,3>>operations;
	for(int i=0;i<t;i++){
		int l,r,v;
		cin >> l >> r >> v;
		operations.push_back({l-1,r,v});
	}

	vector<array<ll,3>>queries;
	for(int i=0;i<q;i++){
		ll l,r,v;
		cin >> l >> r >> v;
		queries.push_back({l-1,r,v});
	}

	vector<int>L(q,0),R(q,t+1); //L ng, R ok
	for(int b=0;b<17;b++){
		vector<vector<int>>query_indices(t+1);
		for(int i=0;i<q;i++)query_indices[(L[i]+R[i])/2].push_back(i);
		atcoder::lazy_segtree<S,op,e,F,mapping,composition,id>seg(vector<S>(n,{0,1}));
		for(int i=0;i<t;i++){
			auto[l,r,v]=operations[i];
			seg.apply(l,r,v);
			for(int qi:query_indices[i+1]){
				auto[l,r,x]=queries[qi];
				if(seg.prod(l,r)[0]>=x)R[qi]=i+1;
				else L[qi]=i+1;
			}
		}
	}
	for(int i=0;i<q;i++)cout << (R[i]==t+1?-1:R[i]) << endl;
}