「いくつかのマスに既に数が書かれていて、残りのマスに数を書き込んでいく」と考える代わりに、「最初どのマスにも数は書かれておらず、全てのマスに数を書き込んでいくが、いくつかのマスについては書き込める数が限定されている」と考えることにします。

動的計画法を用いて、以下の図のように左上から右下の順に各マスに数を書き込んでいき、都度既に数を書き込んだ箇所との整合性をチェックすることを考えます。すなわち、マス \((i,j)\) に数を書き込む際には、\(a_{i,j-1} < a_{i,j}\) および \(a_{i-1,j} < a_{i,j}\) が満たされているかを確認します。

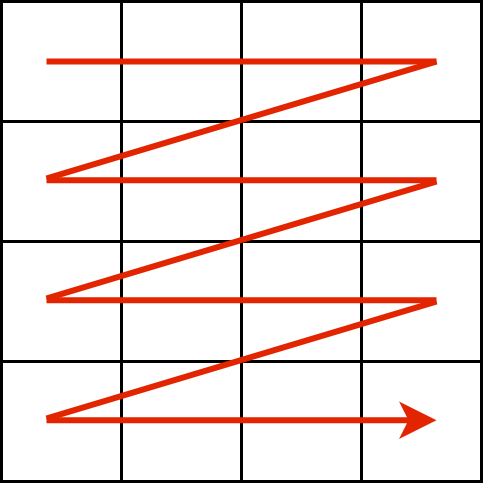
では、この動的計画法を定式化するにあたって、各状態には何の情報を持たせればよいでしょうか？最も簡単なアプローチは、次に数を書き込むマスおよび今までに書き込んだすべての数を情報として持つことです。以下の図はその様子を表しており、次に数を書き込むのが太線で囲まれたマスであるとき、赤く塗られた各マスに書かれた数を情報として持つことになります。

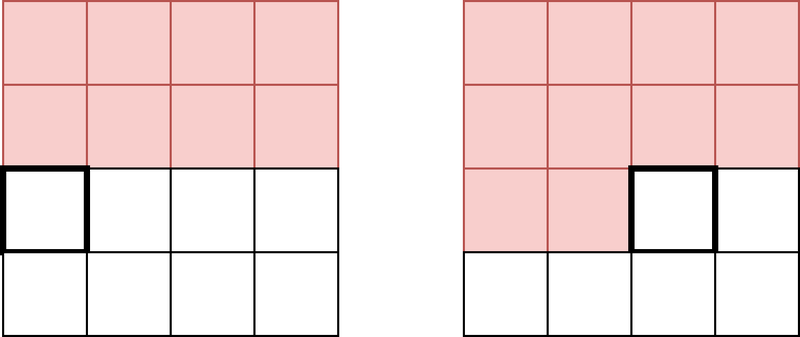
しかし、これではとりうる状態の数が \(16\times M^{16}\) 個ほどになってしまうので、いくつかの状態をまとめる必要があります。

はたして、今までに書き込んだすべての数を情報として持つ必要はあるでしょうか？答えは No です。既に数を書き込んだマスのうち、今後数を書き込むマスとの整合性の確認のために参照されるマス（すなわち、まだ数を書き込んでいないいずれかのマスの左または上に位置するマス）を 重要なマス と呼ぶことにすると、重要なマス以外のマスに書き込まれた数の情報は持つ必要がありません。別の言い方をすると、次に数を書き込むマスの位置および重要な各マスに書き込まれた数が一致しているような状態は同一視してしまってよいです。そして、重要なマスというのは、下図に示されるように、次に数を書き込むマスの直前の（高々）\(4\) マスしか存在しません。

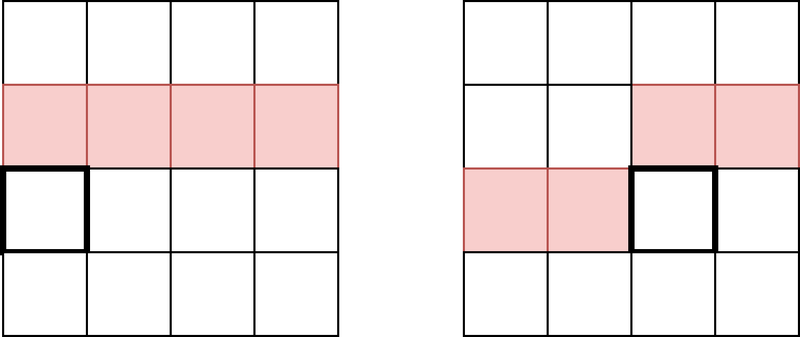
よって、次に数を書き込むマスの位置および直前に書き込んだ \(4\) つの数のみを情報として持つことによって、状態数を \(16\times M^4\) に削減できます。遷移の際には次に書き込む数を \(M\) 通り全て試すことで、全体の計算量は \(16\times M^5\) ほどになり、十分高速です。

実装例 (C++) :

#include <bits/stdc++.h>
#include "atcoder/modint"

using namespace std;
using namespace atcoder;

using mint = modint998244353;

mint dp[4][4][31][31][31][31];

int main() {
    int m;
    cin >> m;
    int a[4][4];
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            cin >> a[i][j];
        }
    }
    dp[0][0][0][0][0][0] = 1;
    mint ans = 0;
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            int ni = i + (j == 3);
            int nj = (j + 1) % 4;
            for (int w = 0; w <= m; w++) {
                for (int x = 0; x <= m; x++) {
                    for (int y = 0; y <= m; y++) {
                        for (int z = 0; z <= m; z++) {
                            mint now = dp[i][j][w][x][y][z];
                            for (int t = 1; t <= m; t++) {
                                if (a[i][j] != -1 and a[i][j] != t) continue;
                                if (z >= t) continue;
                                if (j and w >= t) continue;
                                if (ni < 4) dp[ni][nj][t][w][x][y] += now;
                                else ans += now;
                            }
                        }
                    }
                }
            }
        }
    }
    cout << ans.val() << endl;
}