人 \(1,\ldots,N\) の部分集合を単に添字の集合として表すことにします。つまり、「人 \(1,2,3\) からなる集合」のことを単に \(\{1,2,3\}\) と書いたり表現したりします。

予め \(\{1,\ldots,N\}\) の全ての部分集合 \(S\) に対して、「集合 \(S\) を \(1\) つのグループにして条件を満たすか？」を調べておきます。これは、愚直に条件を確認することで集合 \(1\) つあたり \(O(N+M)\) でできるため、この処理は全体で \(O(N^2 2^N)\) 時間でできます。
関数 \(f_1\) を、\(\{1,\ldots,N\}\) の部分集合から整数への関数であって、\(S\) を \(1\) つのグループにして条件を満たすならば \(1\)、満たさないならば \(0\) と定めます。

次に「\(S\) を \(2\) つのグループにして条件を満たすようにできるか？」を考えてみます。このことは、「ある \(X,Y\) が存在して、\(X\cap Y=\emptyset\) かつ \(X\cup Y=S\) かつ \(f_1(X)=f_1(Y)=1\) となるか？」と同値です。
ところで、ある人が複数のグループに属してもよいとしても答えは変化しません。よって \(1\) 番目の条件は無視することができ、考えるべきは「ある \(X,Y\) が存在して、\(X\cup Y=S\) かつ \(f_1(X)=f_1(Y)=1\) となるか？」となります。
\(f_1\) が 01 値関数であることから、これは「\(\sum_{X\cup Y=S}f_1(X)f_1(Y)\neq 0\) か？」と同値です。ここで、\(f_1\) が与えられたとき全ての \(S\) に対して \(\sum_{X\cup Y=S}f_1(X)f_1(Y)\) を求めることは、高速ゼータ変換を用いた畳み込みにより \(O(N 2^N)\) 時間でできます。（後述）
関数 \(f_2\) を、\(\{1,\ldots,N\}\) の部分集合から整数への関数であって、\(S\) を \(2\) つのグループにして条件を満たすならば \(1\)、満たさないならば \(0\) と定めます。

さらに「\(S\) を \(3\) つのグループにして条件を満たすようにできるか？」は「\(\sum_{X\cup Y=S}f_1(X)f_2(Y)\neq 0\) か？」と同値なので、同様に \(f_1,f_2\) が与えられたとき全ての \(S\) に対してを \(O(N 2^N)\) 時間で計算できます。

以上を繰り返すことで同様に、\(4\) つのグループ、\(5\) つのグループ、……という判定問題を順次 \(O(N 2^N)\) の追加の計算量で求めることができます。求める答えは明らかに \(N\) 以下であることから、この繰り返しは高々 \(O(N)\) 回行えば良く、全体で \(O(N^2 2^N)\) 時間でこの問題を解くことができます。

高速ゼータ変換を用いた畳み込み

まずは次のような問題を考えてみます。

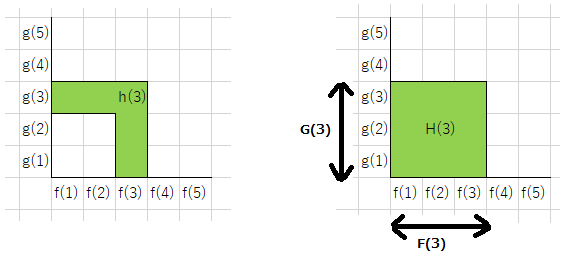
問題：\(f,g\) が与えられるので、\(h(n)=\sum_{\max(x,y)=n}f(x)g(y)\) を全ての \(n\leq N\) で求めよ

愚直に計算すると \(h(n)\) を求めるのに \(O(n)\) 時間かかるため、全体では \(O(N^2)\) 時間かかります。しかし、累積和を用いた次の手法でより高速に計算することができます。

\(h\) の累積和を \(H(m)=\sum_{n\leq m}h(n)\) とします。\(F,G\) についても同様に \(f,g\) の累積和として定めます。このとき \(H(n)=\sum_{\max(x,y)\leq n}f(x)g(y)=F(n)G(n)\) となり、\(H\) は \(F,G\) から \(O(N)\) 時間で求めることができます。\(f,g\) から \(F,G\) を求めることと、\(H\) から \(h\) を求めることは \(O(N)\) 時間でできるため、全体で \(O(N)\) 時間で \(h\) を求めることができました。

元の問題に戻ります。考えているのは次の問題でした。

問題：\(f,g\) が与えられるので、\(h(S)=\sum_{X\cup Y=S}f(S)g(Y)\) を全ての \(S \subset \{1,2,\ldots,N\}\) で求めよ。

先程の問題と全く同様に累積和を考えます。\(H(T)=\sum_{S\subset T}h(S)\) とします。\(F,G\) も同様に定めます。このとき \(H(S)=\sum_{X\cup Y \subset S}f(X)g(Y)=F(S)G(S)\) となり、\(H\) は \(F,G\) から \(O(2^N)\) 時間で求めることができます。よって あとは \(f,g\) から \(F,G\) を求めることと、\(H\) から \(h\) を求めることが高速にできればよいです。

\(f\) から \(F\) を求める操作は多次元累積和にほかならないので、この操作と逆操作は \(O(N 2^N)\) 時間でできます。

(図：\(N=2\) の例)

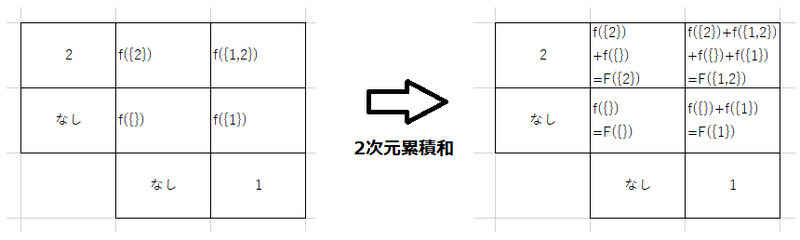
よって、全体で \(O(N 2^N)\) 時間で \(h\) を求めることができました。