問題文

頂点 1, 2, \ldots, N の N 頂点からなる無向グラフがあります。

全ての整数 u, v (1 \leq u < v \leq N) に対し、 u と v が互いに素なとき頂点 u と v の間に辺が張られており、またこれ以外に辺はありません。

頂点 S から頂点 T まで移動するのに通る必要がある辺の個数の最小値を求めてください。

制約

• 2 \leq N \leq 10^{18}
• 1 \leq S, T \leq N
• S \neq T
• 入力は全て整数

入力例 1

4 2 4

出力例 1

2

グラフは以下のようになります。

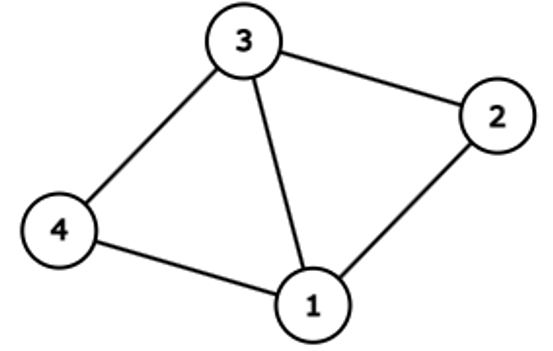
2 \to 3 \to 4 と移動したとき、通る辺の個数は 2 本です。また 1 本以下で移動することはできないため、 2 を出力します。

入力例 2

9999999999 1000000007 998244353

出力例 2

1

入力は 32bit 整数型に収まらない可能性があることに注意してください。