解説

\(N=2,3\)の場合は全探索で解けるため、以下では \(N \geq 4\) とします。

\((1, 2, \dots, N)\) の順列を \(P\) とします。 また、 \(P_i\) と \(P_j\) \((i < j)\) を入れ替えて得られる順列を \(P'\) とします。 このとき、これらの順列の転倒数に関して、以下の式が成り立ちます。 ここで、 \(\mathrm{inv}(P), \mathrm{inv}(P')\) は順列 \(P, P'\) の転倒数です。

\[ \mathrm{inv}(P') = \mathrm{inv}(P) + \begin{cases} 2 \times \#\{ k \in [i, j] \mid P_i < P_k < P_j\} + 1 & (P_i < P_j), \\ - 2 \times \#\{ k \in [i, j] \mid P_i > P_k > P_j\} - 1 & (P_i > P_j). \end{cases} \]

したがって、順列 \(P\) の不安定さは \(P_i, P_j\) の大小関係にかかわらず以下の値になります。

\[ \max_{1 \leq i < j \leq N} 2 \times \#\{ k \in [i, j] \mid \min(P_i, P_j) < P_k < \max(P_i, P_j)\} + 1 \]

すなわち本問題は、 \(M \coloneqq \displaystyle\max_{1 \leq i < j \leq N} \#\{ k \in [i, j] \mid \min(P_i, P_j) < P_k < \max(P_i, P_j)\}\) として、 \(M\) が最小となる \(P\) を一つ出力する問題です。

\(M\) の下界

\(M\) は次のように言い換えることができます。

• \(1\leq i \leq N\) について、二次元座標平面上の \((i,P_i)\) に点がある。
• \(M\) は「 \(1 \leq i < j \leq N\) であって \((i,P_i),(i,P_j),(j,P_j),(j,P_i)\) を頂点とする長方形の内部に存在する点の数」の最大値である。

この座標平面上において \(4\) つの直線 \(x=1,x=N,y=1,y=N\) 上の点集合 \(S\) のみを考えたとき、それらの位置関係のパターンは（上下左右反転で一致するものを除いて）以下の \(4\) つです。

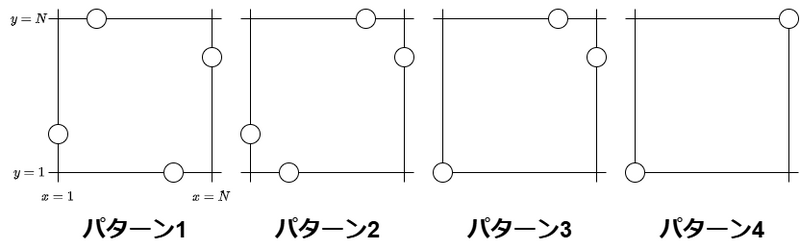
それぞれのパターンについて、以下の図のように「 \(S\) から \(2\) 点選んで作った長方形」いくつかを使って全体を被覆します。 これにより、 \(M\) を下から評価できます。

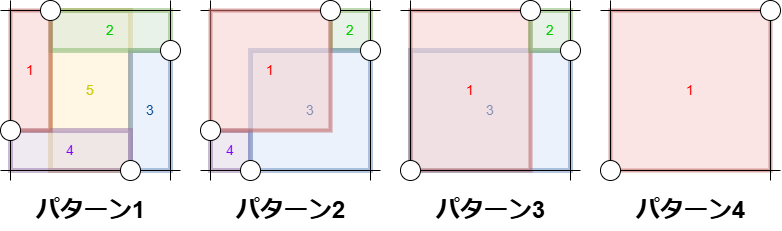
パターン1

このとき、図における長方形 \(i\) の内部に存在する点の数を \(C_i\) とすると、 \(S\) に属さない点は少なくとも一つの長方形の内部にあるため、以下が成り立ちます。

\[ N - 4 \leq C_1 + C_2 + C_3 + C_4 + C_5 \]

一方で、定義より任意の \(i\) について \(M \geq C_i\) です。 したがって、このパターンのとき以下が成り立ちます。

\[ \left\lceil \frac{N-4}{5} \right\rceil \leq \left\lceil \frac{C_1 + C_2 + C_3 + C_4 + C_5}{5} \right\rceil \leq \max_{1 \leq i \leq 5} C_i \leq M. \]

パターン2

パターン1 同様に、このパターンのとき以下が成り立ちます。

\[ \left\lceil \frac{N-4}{4} \right\rceil \leq M. \]

パターン3

パターン1 同様に、このパターンのとき以下が成り立ちます。

\[ \left\lceil \frac{N-3}{3} \right\rceil \leq M. \]

パターン4

パターン1 同様に、このパターンのとき以下が成り立ちます。

\[ \left\lceil \frac{N-2}{1} \right\rceil \leq M. \]

全体の下界

以上より、以下の下界が得られます。

\[ \left\lceil \frac{N-4}{5} \right\rceil \underset{(N \geq 4)}= \min \left( \left\lceil \frac{N-4}{5} \right\rceil, \left\lceil \frac{N-4}{4} \right\rceil, \left\lceil \frac{N-3}{3} \right\rceil, \left\lceil \frac{N-2}{1} \right\rceil \right) \leq M. \]

\(M\) が下界に一致する \(P\) の構成方法

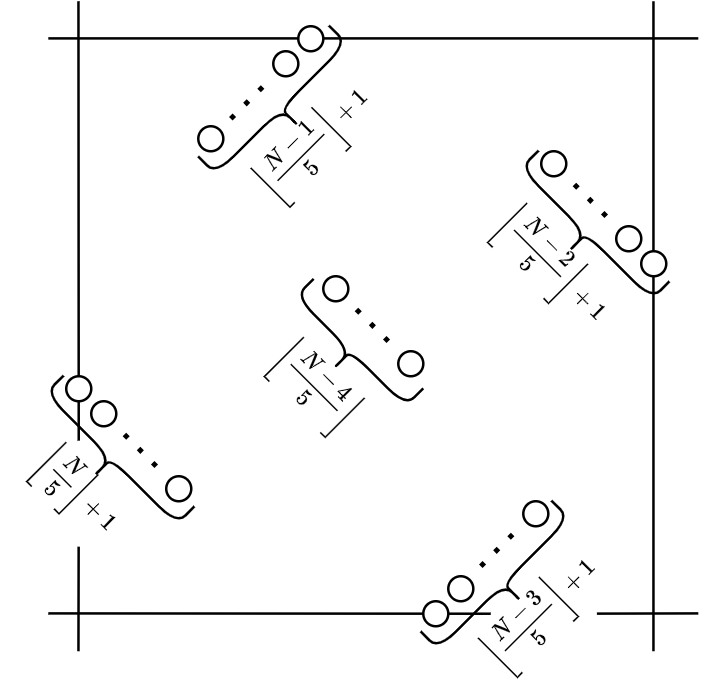
たとえば、下の図のように点を配置することで \(M\) を下界 \(\left\lceil \frac{N-4}{5} \right\rceil\) に一致させることができます。 この配置に対応する順列を出力することで、この問題を正解できます。

クレジット

原案： nu50218

解法： Jinapetto, Levixi

問題準備・解説： Levixi

レビュー： nu50218

テスター： physics0523