この問題は A, B 問題より著しく難易度が高く、水色コーダーや青色コーダーでも苦戦した人がいるのではないかと思います。しかし、最終的には典型的なテクニックを組み合わせることで解くことができるのです。そこで本解説では、

• C 問題「Tricolor Pyramid」の \(O(N^2)\) 解法
• C 問題「Tricolor Pyramid」の \(O(N)\) 解法
• サンプルコード

の 3 つに分けて紹介します。なお、急いで解説を読みたい人は 2-3. 節・2-4. 節をお読みください。

---

1. \(O(N^2)\) 解法

最初に考えられる方針として、各ブロックの色を問題文の通りにを下から順番に計算していく方法が考えられます。

しかし、実装こそ単純ですが、残念ながら \(O(N^2)\) 個のブロックが存在するため、\(N = 400000\) という制約では実行時間超過（TLE）してしまうのです。

一般に、競技プログラミングでは、\(1\) 秒あたり \(10^8\) ～ \(10^9\) 回程度の計算しか許されません。では、さらに高速な解法は存在するのでしょうか。

---

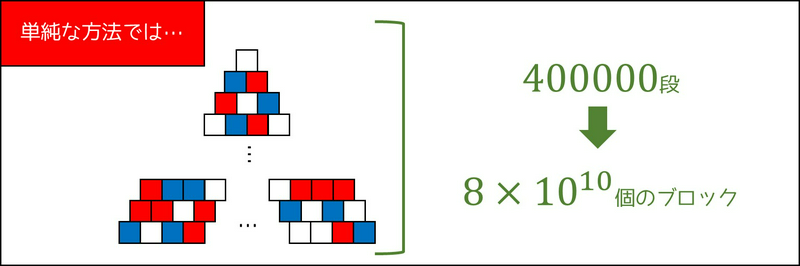
2-1. 考察 1｜整数で表したら上の段はどうなるか？

‘R’・‘W’・‘B’ といった英文字では考察しにくいので、より計算が簡単な形である整数にすることを考えます。例えば、各色に対し、以下のように整数を割り当てます。

• \(c_i =\)‘R’ のとき：\(d_i = 0\)
• \(c_i =\)‘W’ のとき：\(d_i = 1\)
• \(c_i =\)‘B’ のとき：\(d_i = 2\)

そこで、あるブロックの整数は、下の \(2\) つのブロック（左下・右下）の整数にのみ依存し、次の表のようになります。

表をよく観察してみると、下の \(2\) つのブロックの整数を \(p_1, p_2\) とするとき、

• 上のブロックの整数は \(-(p_1 + p_2) \bmod 3\)

になっているのです。（\(\bmod\) は負の数にも拡張でき、例えば \(-2 \bmod 3 = 1, -10 \bmod 3 = 2, -9 \bmod 3 = 0\) です。）

---

2-2. 考察 2｜一番上のブロックの値を \(d_1, d_2, \cdots, d_N\) で表せないか？

そこで、2-1. 節で取り上げた性質を生かせないでしょうか。まずは小さい場合で実験をして、式を立ててみましょう。例えば \(N = 5\) の場合、2-1. 節の式に従って計算すると、次図のようになります。（一番下のブロックを \(d_1, d_2, \cdots d_N\) とし、\(\bmod 3\) は省略しています）

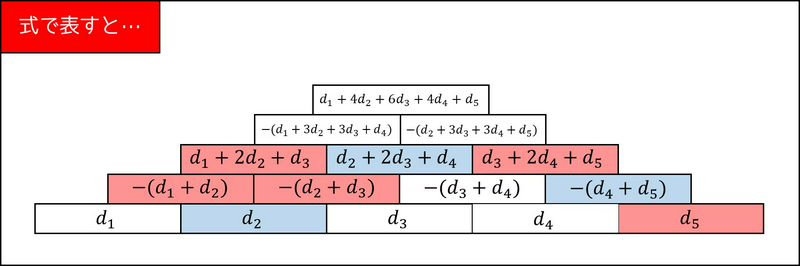
実際、\(N = 1, 2, 3, 4, 5, 6\) の場合の答えは以下の通りです。（\(\bmod 3\) は省略しています）

• \(N = 1\) のとき：\(d_1\)
• \(N = 2\) のとき：\(-(d_1 + d_2)\)
• \(N = 3\) のとき：\(d_1 + 2d_2 + d_3\)
• \(N = 4\) のとき：\(-(d_1 + 3d_2 + 3d_3 + d_4)\)
• \(N = 5\) のとき：\(d_1 + 4d_2 + 6d_3 + 4d_4 + d_5\)
• \(N = 6\) のとき：\(-(d_1 + 5d_2 + 10d_3 + 10d_4 + 5d_5 + d_6)\)

このように手計算を行うと、答えが二項係数やパスカルの三角形に関係しそうなことが分かります。

次に、\(N = 5\) の場合なぜ各項の係数が \((1, 4, 6, 4, 1)\) になるのか考えてみましょう。この理由は次図の通り、経路の通り数の問題に帰着できるからです。重要な事実として、

\(H \times W\) の碁盤目状道路を左上から右下まで最短距離で（右方向か下方向を通って）移動する通り数は \({}_{H+W}C_{H}\) 通り

となることは覚えておきましょう。このような性質を使うことで、

\[ (d_i の項の係数) = (-1)^{N-1} \times {}_{N-1}C_{i-1} \]

であることが分かるのです。

---

2-3. 結論

最後に、2-1. 節・2-2. 節の考察より、最終的な答えは次のようになります。

\[ Answer = \left(-1\right)^{N-1} \times \left(d_1 \begin{pmatrix} N-1 \\ 0 \end{pmatrix} +d_2 \begin{pmatrix} N-1 \\ 1 \end{pmatrix} +d_3 \begin{pmatrix} N-1 \\ 2 \end{pmatrix} +\cdots+d_N \begin{pmatrix} N-1 \\ N-1 \end{pmatrix} \right) \bmod 3 \]

そこで、\(Answer = 0, 1, 2\) の場合それぞれ答えが ‘R’・‘W’・‘B’ となります。ただし、次のような表記は二項係数を表します。（詳しくはこちら）

\[ \begin{pmatrix} n \\ r \end{pmatrix} ={}_nC_{r} = \frac{n!}{r!(n-r)!} \]

詳しくは 2-5. 節で述べますが、\({}_{N-1}C_{i-1} \bmod 3\) の値は \(O(1)\) で計算できるので、全体計算量は \(O(N)\) となり、十分高速に実行が終わります。

---

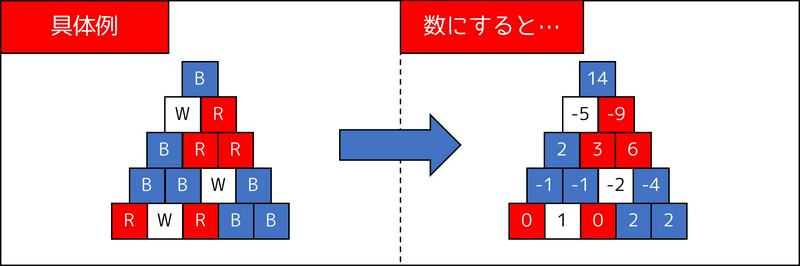
2-4. 具体例

例えば \(c_1c_2c_3 \cdots c_N = \)RWRBB の場合、\((d_1, d_2, d_3, d_4, d_5) = (0, 1, 0, 2, 2)\) となり、

\[ (-1)^{4} \times \left( 0 \times \begin{pmatrix} 4 \\ 0 \end{pmatrix} + 1 \times \begin{pmatrix} 4 \\ 1 \end{pmatrix} + 0 \times \begin{pmatrix} 4 \\ 2 \end{pmatrix} + 2 \times \begin{pmatrix} 4 \\ 3 \end{pmatrix} + 2 \times \begin{pmatrix} 4 \\ 4 \end{pmatrix} \right) = 1 \times \left(0 + 4 + 0 + 8 + 2\right) = 14 \]

であるため、\(14 \bmod 3 = 2\) より、一番上の答えは B となります。

---

2-5. 補足｜どうやって \({}_nC_{r} \bmod 3\) を計算するか？

この問題は \(\bmod 10^9+7\) ではなく \(\bmod 3\) での二項係数の値を求める必要があるため、逆元を使った手法を用いることができません。

代わりに、以下の \(2\) つの値を計算することを考えます。

• \(f(N)\)：\(N\) が \(3\) で何回割れるか（例：\(f(117) = 2, f(260) = 0, f(729) = 6\)）
• \(g(N)\)：\(N\) を \(3\) の倍数でなくなるまで割ってできた整数を、\(3\) で割った余り（例：\(g(117) = 1, g(260) = 2, g(729) = 1\)）

このとき、\({}_nC_{r} = \frac{n!}{r!(n-r)!}\) を \(3\) で割った余りは次のようになります。

• \(f(n!) - f(r!) - f((n-r)!) \geq 1\) の場合：
  • 明らかに \(3\) の倍数であり、必ず余りは \(0\) となる
• \(f(n!) - f(r!) - f((n-r)!) = 0\) の場合：
  • \(g(n!) = 1, g(r!) \times g((n-r)!) = 1\) のとき：余り \(1\)
  • \(g(n!) = 1, g(r!) \times g((n-r)!) = 2\) のとき：余り \(2\)
  • \(g(n!) = 1, g(r!) \times g((n-r)!) = 4\) のとき：余り \(1\)
  • \(g(n!) = 2, g(r!) \times g((n-r)!) = 1\) のとき：余り \(2\)
  • \(g(n!) = 2, g(r!) \times g((n-r)!) = 2\) のとき：余り \(1\)
  • \(g(n!) = 2, g(r!) \times g((n-r)!) = 4\) のとき：余り \(2\)

したがって、整数 \(N\) が与えられたとき、\(f(N!), g(N!)\) の値が分かれば良いことになります。次にこれをどうやって計算するか説明します。

\(f(N!)\) の値を求める

前提として、次の式が成り立ちます。

\[ f(N!) = f(1) + f(2) + f(3) + \cdots + f(N) \]

したがって、最初に \(f(1), f(2), \cdots, f(N)\) それぞれの値を計算し、次に累積和を取れば良いです。累積和は次のような実装で計算することができます。

1. まず \(a_i = f(i)\) を前計算しておく。
2. 次に \(b_0 = 0\) とする。
3. 最後に \(i = 1, 2, 3, \cdots, N\) の順に \(b_i = b_{i-1} + a_i\) とする。

そうすると、\(b_i = f(1) + f(2) + \cdots + f(N)\) となります。

\(g(N!)\) の値を求める

前提として、次の式が成り立ちます。

\[ g(N!) = g(1) \times g(2) \times g(3) \times \cdots \times g(N) \bmod 3 \]

したがって、最初に \(g(1), g(2), g(3), \cdots, g(N)\) それぞれの値を計算し、次に累積積を取れば良いです。累積積は次のような実装で計算することができます。

1. まず \(a_i = g(i)\) を前計算しておく。
2. 次に \(b_0 = 1\) とする。
3. 最後に \(i = 1, 2, 3, \cdots, N\) の順に \(b_i = (b_{i-1} \times a_i) \bmod 3\) とする。

そうすると、\(b_i = g(1) \times g(2) \times \cdots \times g(N) \bmod 3\) となります。

計算量はどうなるか？

最後に、\(f(1), f(2), \cdots, f(N), g(1), g(2), \cdots, g(N)\) を計算するのにどれくらい時間がかかるのでしょうか。

• 適当に整数を選んだとき、\(3\) で割れる回数の平均は \(1.5\)

であるため、一番単純な形でプログラムを書いても、\(1\) つの整数 \(i\) に対して \(f(i)\) または \(g(i)\) を計算するのに \(1.5\) 回程度（定数）かかります。したがって全体計算量は \(O(1) \times N = O(N)\) となります。

---

3. サンプルコード

C++ での解答例は次のようになります。（リンク）

#include <iostream>
using namespace std;

long long bf[1 << 19];
long long bg[1 << 19];

void init() {
	for (int i = 1; i <= 400000; i++) {
		int pos = i;
		while (pos % 3 == 0) { pos /= 3; bf[i] += 1; }
		bg[i] = pos % 3;
	}
	bg[0] = 1;
	for (int i = 1; i <= 400000; i++) bf[i] += bf[i - 1];
	for (int i = 1; i <= 400000; i++) bg[i] = (bg[i] * bg[i - 1]) % 3;
}

int ncr_mod_3(int n, int r) {
	if (bf[n] != bf[r] + bf[n - r]) return 0;
	if (bg[n] == 1 && bg[r] * bg[n - r] == 1) return 1;
	if (bg[n] == 1 && bg[r] * bg[n - r] == 2) return 2;
	if (bg[n] == 1 && bg[r] * bg[n - r] == 4) return 1;
	if (bg[n] == 2 && bg[r] * bg[n - r] == 1) return 2;
	if (bg[n] == 2 && bg[r] * bg[n - r] == 2) return 1;
	if (bg[n] == 2 && bg[r] * bg[n - r] == 4) return 2;
	return -1;
}

int main() {
	int N; string S;
	cin >> N >> S;
	init();

	int ret = 0;
	for (int i = 0; i < N; i++) {
		int p1 = 0, p2 = ncr_mod_3(N - 1, i);
		if (S[i] == 'B') p1 = 0;
		if (S[i] == 'W') p1 = 1;
		if (S[i] == 'R') p1 = 2;
		ret += p1 * p2;
		ret %= 3;
	}
	if (N % 2 == 0) ret = (3 - ret) % 3;

	if (ret == 0) cout << "B" << endl;
	if (ret == 1) cout << "W" << endl;
	if (ret == 2) cout << "R" << endl;
	return 0;
}