以降あなたを貴とする。貴の初期頂点を \(x\), 初期の鬼までの距離を \(d_0\) とする。 詳しい解法は略解の次に書かれている。

略解

貴は \(x\) から一番遠い点に向かって出来るだけ進む。やばくなったら一歩戻ってそこから出来るだけ遠いところに逃げる。やばい条件は、鬼との距離が \(2\) 以下のとき。ただし、図 1 のようなとき、(\(d_0\) が偶数で鬼と距離 \(2\) になったときの貴の頂点から深さ \(d_0\) の木が生えているとき)、矢印の方向に進む。 以上は直径の端点からの LCA と全方位木 DP を用いると実装できる。

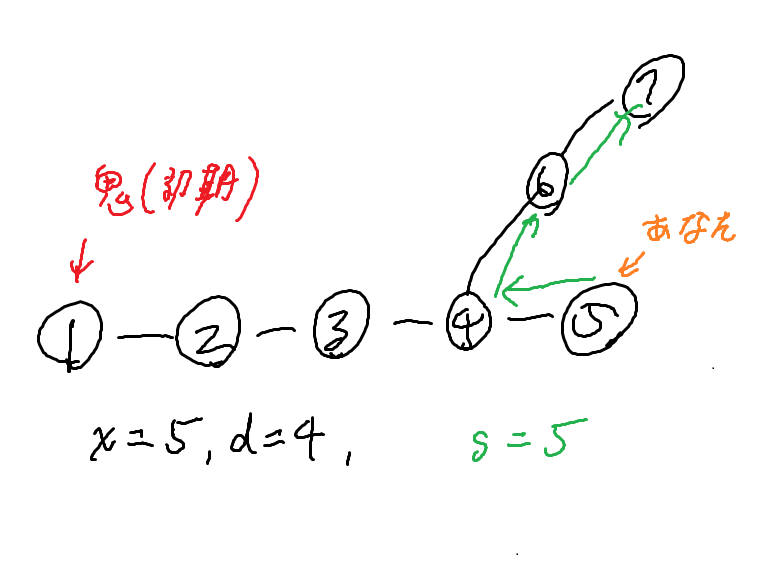
詳細解法

\(d_0=1\) のときは、答えは \(1\)。\(d_0=2\) のときは置いといて、\(3 \leq d_0\) のときを考える。

適当な木の直径の端点のうち \(x\) から遠い方の点を \(p\) とする。すると、\(p\) は \(x\) から一番遠い頂点の一つとなる。これは木の直径を求めるアルゴリズムからもわかる。貴は以下の操作を行うとき最適となる。 \(t\) 秒経った後の鬼までの距離を \(d(t)\) とする。

1. \(d(t)>2\) のときは、\(p\) に向かって進み続ける。\(p\) に着けばそこで鬼と出会うまで停止、着く前に \(d(t) \leq 2\) となったときは次の操作に進む。
2. \(d(t) = 2\) のとき、貴が今いる頂点 \(a\) で木を分割する。それぞれの木の根は \(a\) とする。\(x\) を含む部分木の深さが \(d/2 - 1\) であり、深さ \(d/2\) の部分木があるとき、深さ \(d/2\) の部分木の一番深い頂点に向かって、そこで静止。
3. 上記以外の時は \(x\) を含む部分木の一番深い頂点に向い、着いたら静止。

この一連の操作 S が最適であることを示す。 つまり、まず、操作 2,3 をするとき鬼と出会うまでの時間が最小(\(x\), \(d_0\) が同じで操作 1 のみで終わるときの出会う時間以下)となることを示し、次に、鬼の初期頂点がある頂点のとき、操作 S をすると、操作 2,3 をすることになり、ほかの操作は操作 S をしたときより早く、もしくは同じ時間で鬼と出会うことを示す。

頂点 \(x\) から頂点 \(p\) 方向に距離 \(\lfloor \frac{d_0-1}{2} \rfloor - 1\) の頂点を \(u\), 距離 \(\lfloor \frac{d_0-1}{2} \rfloor\) の頂点を \(v\), 距離 \(d_0 - \lfloor \frac{d_0-1}{2} \rfloor\) の頂点を \(w\) とする。また、鬼の初期位置を \(z\) とする。頂点 \(a,b\) の距離を \(dis(a,b)\) とする。

操作 2 で終わるときは、鬼と出会うまでの時間は \(d_0 + 1\)、操作 1 で終わるとき、貴は頂点 \(p\) まで移動した後 2 秒以上待つ。制約から \(dis(x,p) \geq d_0\)、操作 1 で終わるときより操作 2 で終わるときの方が短時間で鬼に捕まる。 操作 1 で終わるときより操作 3 の方が早く、もしくは同じ時間で捕まることについては、下図のように鬼の初期位置を変えることで、示される。

次に、ほかの操作についても考える。辺 \((u,v)\) を切ったとき頂点 \(v\) を含む部分木上に鬼がいたとき、上記操作では、操作 2,3 で終わる。上記操作を行ったとき、\(d(t) \leq 2\) となる最小整数の \(t\) を \(t_b\) とし、そのときに貴のいる頂点を \(y(t_b)\) とすると、\(y(t_b)=v\) である。 \(t_b\) 秒までの間で得られている情報は、頂点 \(v\) で分割し、頂点 \(u\) を含まない部分木集合 \(A\) のうち深さが \(d_0 - \lfloor \frac{d_0-1}{2} \rfloor\) 以上の部分木上で頂点 \(v\) から距離 \(d(t_b)\) にある頂点のいずれかに鬼がいる。ほかの操作をしても、\(t_b\) 秒以内では、必ず頂点 \(u\) を含む部分木上にいるので、この鬼の位置の候補を絞ることはできない。よって、どの操作をしても、この鬼の位置の候補がある方向には行けない(行くと操作 S を行うときよりも出会う時間が早くなる)。

\(d_0\) が奇数の時、\(d(t_b)=1\) であり、\(A\) のうち深さ \(\frac{d_0+1}{2}\) 以上の部分木には行けない。また、頂点 \(u\) を含む部分木の深さは \(dis(x,v) = \frac{d_0-1}{2}\) 以上であるので、\(y(t_b)=v\) のとき操作 3 が最適となる。また、\(y(t_b) \neq v\) のときは行くことができる頂点が減少するので、操作 3 が最適となる。

\(d_0\) が偶数の時、\(d(t_b)=2\) であり、\(A\) のうち深さ \(\frac{d_0}{2}+1\) 以上の部分木には行けない。また、頂点 \(u\) を含む部分木の深さは \(dis(x,v) = \frac{d_0}{2} - 1\) 以上であるので、\(y(t_b)=v\) のとき操作 2,3 が最適となる。また、\(y(t_b) \neq v\) のときは行くことができる頂点が減少するので、操作 2,3 が最適となる。

よって示された。 \(d_0=2\) のときは操作 2,3 と同様の操作をする。

実装については、事前に直径の端点を根とする LCA 2 つと、全方位木 DP でそれぞれの頂点に対しその頂点で分割したときの部分木の深さの集合を持って置き、LCA から \(u,v\) を計算し、部分木の深さの集合から深さ \(d_0/2\) の部分木があるかどうかを調べればよい。 計算量は \(O(q \log n)\)