/
/ 
実行時間制限: 2.5 sec / メモリ制限: 128 MiB
配点: 100 点
JOI 国には N 個の街があり,それらの間は M 本の双方向に通行可能な道路で結ばれている.国民は道路を通ってそれらの街を移動する.
JOI 国の国民には,お祭りが好きな人が多く,現在,K 個の街でお祭りが開催されており,非常に賑わっている.一方で,一部の国民はお祭りを騒がしいとして嫌い,お祭りにできるだけ近づきたくないと思っている.
そこで国王は,優秀なプログラマーであるあなたに,そのようなお祭りを嫌う国民のため,ある街からある街に移動するために,お祭りが開催されている街にどれだけ近づかずに移動することができるかを高速に調べることのできるプログラムの作成を依頼した.
課題
道路の情報とお祭りが開催されている街の情報,および Q 個のクエリ(出発する街 S_i と行きたい街 T_i の組)が与えられる.各クエリ i に対し,街 S_i から街 T_i へのすべての経路のうち,お祭りまでの距離が最大となる経路の,お祭りまでの距離を求めるプログラムを作成せよ.ただし,ある経路のお祭りまでの距離とは,経路上の街からお祭りが開催されている街までの移動距離の最小値のことである.
制限
| 2 \leqq N \leqq 100000 \,(= 10^5) | JOI 国の街の個数 |
| 1 \leqq M \leqq 200000 \,(= 2\times 10^5) | JOI 国の道路の本数 |
| 1 \leqq K \leqq N | お祭りが開催されている街の個数 |
| 1 \leqq Q \leqq 100000 \,(= 10^5) | クエリの個数 |
| 1 \leqq L_i \leqq 1000 | i 番目の道路の長さ |
入力
標準入力から以下のデータを読み込め.
- 1 行目には整数 N, M, K, Q が空白を区切りとして書かれている.N は JOI 国の街の個数を,M は JOI 国の道路の本数を,K はお祭りが開催されている街の個数を,Q はクエリの個数をそれぞれ表す.街には 1,2,\ldots,N の番号がつけられている.
- 続く M 行は道路の情報を表す.i + 1 行目 (1\leqq i\leqq M) には整数 A_i,B_i,L_i (1\leqq A_i\leqq N,1\leqq B_i\leqq N) が空白を区切りとして書かれている.これは,i 番目の道路が街 A_i と街 B_i を結んでおり,長さが L_i であることを表す.道路の両端が同じ街であることはない.また,任意の 2 つの街 p, q に対し,p と q を結ぶ道路は 2 本以上存在しない.どの街からどの街へもいくつかの道路をたどって行くことができる.
- 続く K 行はお祭りが開催されている街の情報を表す.i + M + 1 行目 (1\leqq i\leqq K) には 1 つの整数 F_i (1\leqq F_i\leqq N) が書かれている.これは街 F_i でお祭りが開催されていることを表す.F_1,\ldots,F_K の中に同じ値が 2 回以上現れることはない.
- 続く Q 行はクエリを表す.i + M + K + 1 行目 (1\leqq i\leqq Q) には 2 つの整数 S_i,T_i (1\leqq S_i\leqq N,1\leqq T_i\leqq N, S_i\neq T_i) が空白を区切りとして書かれている.これは i 番目のクエリの出発する街が S_i であり行きたい街が T_i であることを表す.
出力
標準出力に,全クエリへの答えを Q 行で出力せよ.すなわち,i 行目に,街 S_i から街 T_i へのすべての経路のうち,お祭りまでの距離が最大となる経路の,お祭りまでの距離を表す整数を出力せよ.
採点基準
採点用データのうち,
配点の 10 %分については,Q=1 を満たす.
配点の 20 %分については,N\leqq 5000,Q\leqq 5000 を満たす.
配点の 30 %分については,これら 2 つの条件の少なくとも一方を満たす.また,これら 2 つの条件の両方を満たすような採点用データはない.
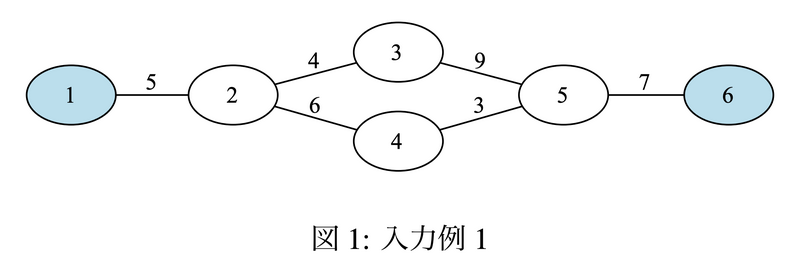
入力例 1
6 6 2 3 1 2 5 2 3 4 2 4 6 3 5 9 4 5 3 5 6 7 1 6 3 4 5 2 1 4
出力例 1
7 5 0
6 つの街が 6 本の道路で結ばれており,お祭りは街 1, 6 の 2 つの街で開催されている.クエリは以下の 3 つである.
- 1 つ目のクエリは街 3 から街 4 へ行くというものである.街 2 を経由する経路ではお祭りまでの距離は 5,街 5 を経由する経路ではお祭りまでの距離は 7 となるため,答えは 7 である.
- 2 つ目のクエリは街 5 から街 2 へ行くというものである.街 3 と街 4 のどちらを経由しても,街 2 でお祭りまでの距離が最小となり,答えは 5 である.
- 3 つ目のクエリは街 1 から街 4 へ行くというものである.街 1 はお祭りが開催されている街であるため,答えは 0 となる.