 /
/ 
Time Limit: 500 msec / Memory Limit: 64 MiB
配点: 100 点
JOI 国には N 個の町があり,それらの間は M 本の双方向に通行可能な道路で結ばれている.K 個の町にはショッピングモールがあり,国民は道路を通ってそれらの町のいずれかに行き買い物をする.
家の場所によっては,買い物に行くために長い距離を移動する必要があり,それは非常に不便である.国王はこの実情を把握するため,ショッピングモールのある町までの最短距離が家の場所によってどれだけ長くなりうるのかを調べることにした.家は道路の途中に建てられることもあるので (入力例 1 の説明を参 照),この調査は非常に大変である.そこで国王は,優秀なプログラマーであるあなたに,調査を行うプログラムの作成を依頼した.
課題
道路の情報とショッピングモールのある町の情報が与えられるとき,ショッピングモールのある町からもっとも遠い道路上の点 (端点も含む) までの距離を求めるプログラムを作成せよ.町の中を移動するのにかかる距離は無視してよい.
制限
| 2 \leqq N \leqq 3\,000 | JOI 国の町の個数 |
| 1 \leqq M \leqq 100\,000\, (=10^5) | JOI 国の道路の本数 |
| 1 \leqq K\leqq N | ショッピングモールがある町の個数 |
| 1 \leqq l_i \leqq 1\,000 | i 番目の道路の長さ |
入力
標準入力から以下の入力を読み込め.
- 1 行目には整数 N, M, K が空白区切りで書かれている.N は JOI 国の町の個数を,M は JOI 国の道路の本数を,K はショッピングモールがある町の個数をそれぞれ表す.町には 1,2,\ldots,N の番号がつけ られている.
- 続く M 行は道路の情報を表す.i + 1 行目 (1\leqq i \leqq M) には整数 a_i,b_i,l_i (1\leqq a_i\leqq N,1\leqq b_i\leqq N,1\leqq l_i\leqq 1000) が空白区切りで書かれている.これは,i 本目の道路が町 a_i と町 b_i を結んでおり,長さが l_i であることを表す.道路の両端が同じ町であることはない.また,任意の 2 つの町 p, q に対し,p と q を結ぶ道路は 2 本以上存在しない.どの町からどの町へもいくつかの道路をたどって行くことができる.
- 続く K 行はショッピングモールの情報を表す.i + M + 1 行目 (1 \leqq i \leqq K) には 1 つの整数 s_i (1 \leqq s_i \leqq N) が書かれている.これは町 s_i にショッピングモールがあることを表す. s_1,\ldots, s_K の中に同じ値が 2 回以上現れることはない.
出力
標準出力に,ショッピングモールのある町までの最短距離の最大値の小数点以下を四捨五入した整数 1 つを出力せよ.
採点基準
採点用データのうち,配点の 40 %分については,K = 1 を満たす.
入力例 1
3 3 1 1 2 1 2 3 1 3 1 1 1
出力例 1
2
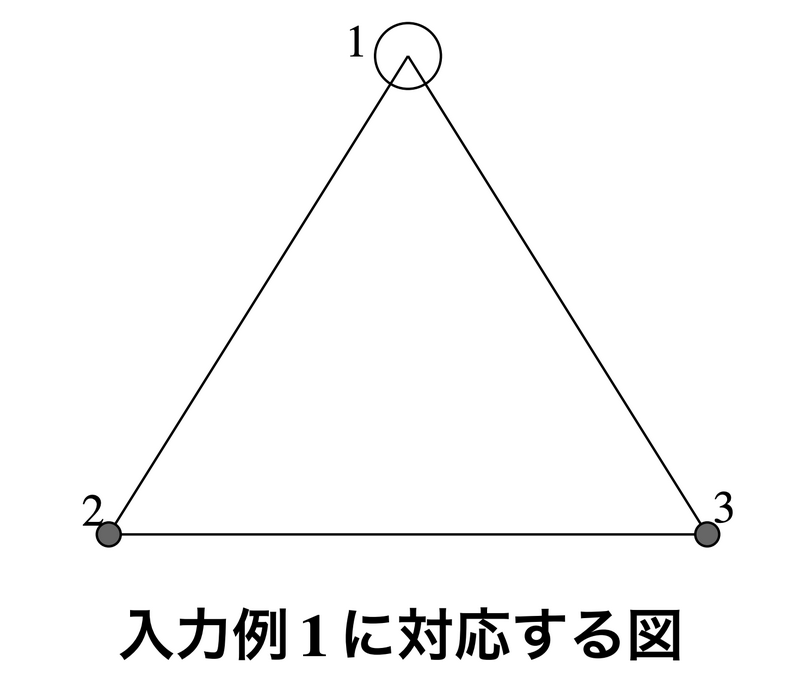
入力例 1 は次のような町を表す.道路の長さはすべて 1 である.ショッピングモールは町 1 にしかない.
ショッピングモールのある町までもっとも遠い点は,町 2 と町 3 を結ぶ道路上の,町 2 から距離 0.5 の位置にある点であり,ショッピングモールのある町までの距離は 1.5 である.よって,それを四捨五入した値である 2 を出力する.
入力例 2
4 5 2 1 2 4 1 3 1 2 3 2 2 4 2 3 4 1 2 4
出力例 2
3