Problem Statement

Japanese Animal Girl Library (JAG Library) is famous for a long bookshelf. It contains $N$ books numbered from $1$ to $N$ from left to right. The weight of the $i$-th book is $w_i$.

One day, naughty Fox Jiro shuffled the order of the books on the shelf! The order has become a permutation $b_1, \ldots, b_N$ from left to right. Fox Hanako, a librarian of JAG Library, must restore the original order. She can rearrange a permutation of books $p_1, \cdots, p_N$ by performing either operation A or operation B described below, with arbitrary two integers $l$ and $r$ such that $1 \le l < r \le N$ holds.

Operation A:

• A-1. Remove $p_l$ from the shelf.
• A-2. Shift books between $p_{l+1}$ and $p_r$ to left.
• A-3. Insert $p_l$ into the right of $p_r$.

Operation B:

• B-1. Remove $p_r$ from the shelf.
• B-2. Shift books between $p_l$ and $p_{r-1}$ to right.
• B-3. Insert $p_r$ into the left of $p_l$.

This picture illustrates the orders of the books before and after applying operation A and B for $p=(3,1,4,5,2,6)$, $l=2$, $r=5$.

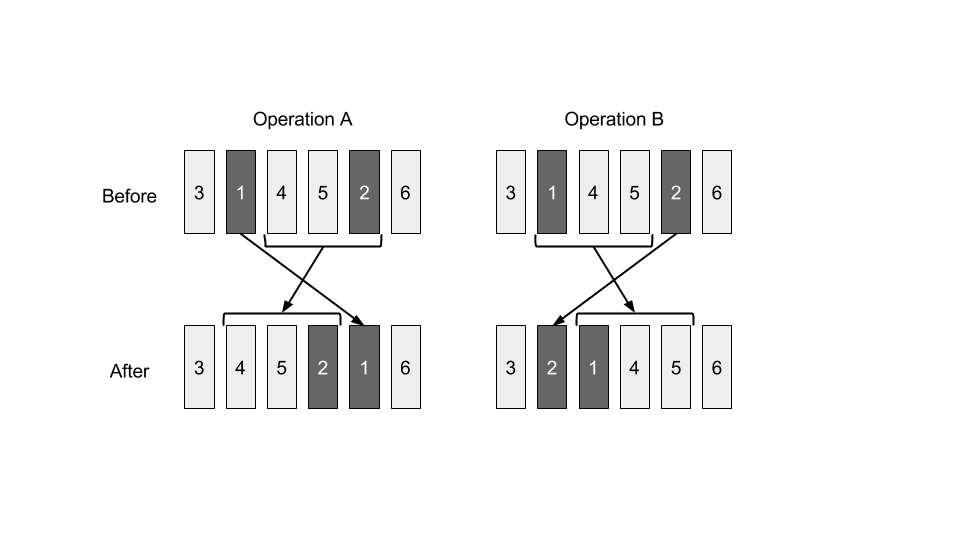
Since the books are heavy, operation A needs $\sum_{i=l+1}^{r} w_{p_i} + C \times (r-l) \times w_{p_l}$ units of labor and operation B needs $\sum_{i=l}^{r-1} w_{p_i} + C \times (r-l) \times w_{p_r}$ units of labor, where $C$ is a given constant positive integer.

Hanako must restore the initial order from $b_1, \cdots, b_N$ by performing these operations repeatedly. Find the minimum sum of labor to achieve it.

---

Input

The input consists of a single test case formatted as follows.

$N \ C$ $b_1 \ w_{b_1}$ $\vdots$ $b_N \ w_{b_N}$

The first line conists of two integers $N$ and $C \ (1 \le N \le 10^5, 1 \le C \le 100)$. The $(i+1)$-th line consists of two integers $b_i$ and $w_{b_i} \ (1 \le b_i \le N, 1 \le w_{b_i} \le 10^5)$. The sequence $(b_1, \ldots, b_N)$ is a permutation of $(1, \ldots, N)$.

Output

Print the minimum sum of labor in one line.

---

Sample Input 1

3 2
2 3
3 4
1 2

Output for Sample Input 1

15

Performing operation B with $l=1, r=3$, i.e. removing book 1 then inserting it into the left of book 2 is an optimal solution. It costs $(3 + 4) + 2 \times 2 \times 2 = 15$ units of labor.

---

Sample Input 2

3 2
1 2
2 3
3 3

Output for Sample Input 2

0

---

Sample Input 3

10 5
8 3
10 6
5 8
2 7
7 6
1 9
9 3
6 2
4 5
3 5

Output for Sample Input 3

824