C - Containers
Editorial
 /
/ 
The land is separated into 1 \times 1 cells. Each of the containers is on one of the cells.
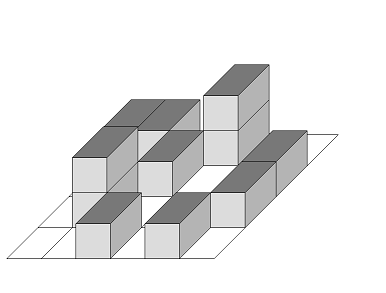
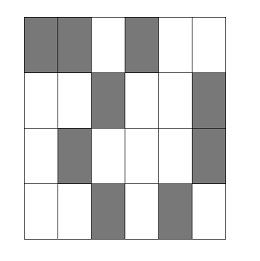
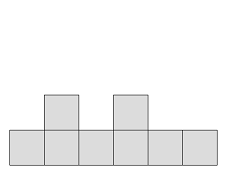
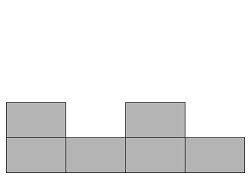 Given the photograph from the sky, front, and side respectively, calculate how many containers are piled up in the minimum.
Given the photograph from the sky, front, and side respectively, calculate how many containers are piled up in the minimum.
Each of the following H lines gives the photograph from the sky.
The value of u_{ij} means,
The next line gives the photograph from the front.
The integer f_i is the number of the containers seen in i-th row.(0 \leq f_i \leq 100)
The next line gives the photograph from the side.
The integer s_i is the number of the containers seen in i-th column.(0 \leq s_i \leq 100)
Output the minimum number of the containers.
If the photographs are inconsistent, just output
 /
/ 
Time Limit: 1.5 sec / Memory Limit: 93 MB
Description
Some 1 \times 1 \times 1 containers are piled up in land of W \times H.The land is separated into 1 \times 1 cells. Each of the containers is on one of the cells.

Figure 1

Figure 2: from The Sky

Figure 3: from The Front

Figure 4: from The Side
Input
H W
u_{11} u_{12} … u_{1W}
u_{21} …
:
:
u_{H1} u_{H2} … u_{HW}
f_1 f_2 … f_W
s_1 s_2 … s_H
The first line of the input file contains the integers H and W (1 \leq H,W \leq 100), the number of height and width of the land.Each of the following H lines gives the photograph from the sky.
The value of u_{ij} means,
0: no containers are piled up in (i, j), 1: some containers are piled up in (i, j).The next line gives the photograph from the front.
The integer f_i is the number of the containers seen in i-th row.(0 \leq f_i \leq 100)
The next line gives the photograph from the side.
The integer s_i is the number of the containers seen in i-th column.(0 \leq s_i \leq 100)
Output
If the photographs are inconsistent, just output
-1, instead.Sample Input
2 3 0 1 0 1 1 1 2 3 2 2 3
Sample Output
9
Sample Input
4 6 1 1 0 1 0 0 0 0 1 0 0 1 0 1 0 0 0 1 0 0 1 0 1 0 1 2 1 2 1 1 2 1 2 1
Sample Output
11