C - ポーター・テレ・ポーター (Porter-Tele-Porter) Editorial /

Time Limit: 0 msec / Memory Limit: 256 MB

あなたはポーター・テレ・ポーターというロールプレイングゲームをプレイしている。

このゲームには、二つの正方形の陸マップと海マップがある。一辺の長さは陸マップがE、海マップがSであり、E＜Sである。
また、マップ上の地点は東向きをX軸、北向きをY軸として座標(X,Y)で表される。原点はマップの最も南西にある地点である．

２つのマップは下の図のように繋がっている。
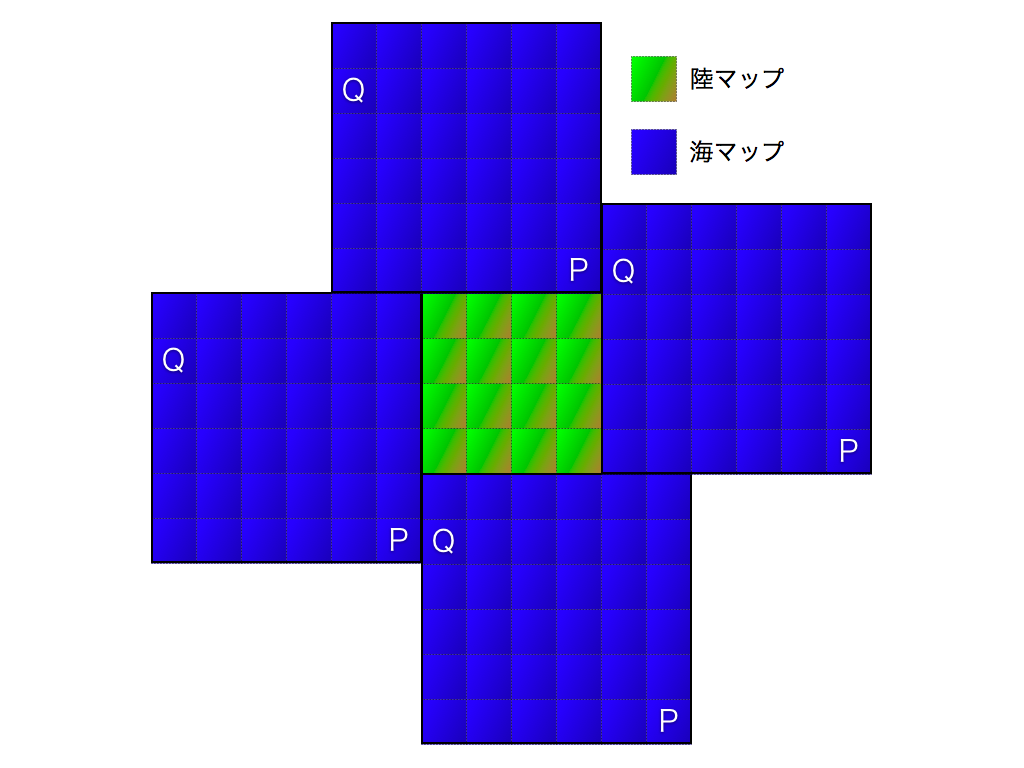
porter-fig1.png
この図での海マップは全て同じものを表している。例えば、図中のP点から東に１歩進むとQ点に到達する。

このゲームではあなたはポーター（荷物運搬人）というキャラクターとして行動する。
ポーターはマップ上で東西南北のいずれかの向きを向いていて，陸と海のどちらもマップ上も移動できる。

ゲームが始まった時、ポーターは陸マップの(0,0)にいて、ポーターには荷物を運ぶ目的地を表す陸マップの座標(X,Y)と、テレポーター(A,B)という装置が与えられる。
テレポーター(A,B)のスイッチを押すと、今いる位置からA歩前進し左に曲がってB歩前進したときの位置に一瞬で移動することができる。

ポーターは疲れたくないので、与えられたテレポーター(A,B)と方向転換だけを使って目的地(X,Y)へ移動したいと考えている。
テレポーターと方向転換だけで移動することが不可能な場合、ポーターは徒歩または泳ぎで目的地(X,Y)に移動する。

何らかの方法でポーターが目的地(X,Y)に到達すると、そこで新たな目的地の座標とテレポーターが与えられ、ゲームは続行する。
新たな目的地への移動では新たに与えられたテレポーターを使い、もともと持っていたテレポーターは使うことができない。

あなたは、目的地のそれぞれに行く過程において、ポーターがテレポーターと方向転換だけで目的地にたどり着けるか、またそのとき何回テレポーターを使えば良いかを知りたくなった。

課題

一辺の長さEの正方形の陸のマップと、一辺の長さSの正方形の海のマップがある。 二つのマップ上の点は座標で表され、海のマップでは (Sx,Sy)(Sx,Syは整数、0≦Sx＜S,0≦Sy＜S)、陸のマップでは(Ex,Ey)(Ex,Eyは整数、0≦Ex＜E,0≦Ey＜E)である。

この時、東西南北４方向への一歩の移動を次のように定義する。(注意：x軸は東向き、y軸は北向きである。)

  • 陸の東端(E-1,y)から東に進むと海の西端(0,y)に出て、海の西端(0,y)から西に進むと陸の東端(E-1,y)に出る。(0≦y＜E)
  • 陸の南端(x,0)から南に進むと海の北端(x,S-1)に出て、海の北端(x,S-1)から北に進むと陸の南端(x,0)に出る。(0≦x＜E)
  • 陸の西端(0,y)から西に進むと海の東端(S-1,S-E+y)に出て、海の東端(S-1,S-E+y)から東に進むと陸の西端(0,y)に出る。(0≦y＜E)
  • 陸の北端(x,E-1)から北に進むと海の南端(S-E+x,0)に出て、海の南端(S-E+x,0)から南に進むと陸の北端(x,E-1)に出る。(0≦x＜E)
  • 海の西端(0,E+y)から西に進むと海の東端(S-1,y)に出て、海の東端(S-1,y)から東に進むと海の西端(0,E+y)に出る。(0≦y＜S-E)
  • 海の北端(E+x,S-1)から北に進むと海の南端(x,0)に出て、海の南端(x,0)から南に進むと海の北端(E+x,S-1)に出る。(0≦x＜S-E)
  • 上のいずれの場合にも当てはまらないとき、
    • 陸の(x,y)から、東に進むと陸の(x+1,y)、南に進むと陸の(x,y-1)、西に進むと陸の(x-1,y)、北に進むと陸の(x,y+1)に出る。(0≦x＜E、0≦y＜E)
    • 海の(x,y)から、東に進むと海の(x+1,y)、南に進むと海の(x,y-1)、西に進むと海の(x-1,y)、北に進むと海の(x,y+1)に出る。(0≦x＜S、0≦y＜S)

また、キャラクターがいる位置と向きからA歩前に進み、左に曲がってB歩前に進むことを、合わせてテレポーター(A,B)を使うと定義する。

次のプロシージャを実装せよ:

  • 次のパラメータを持つプロシージャ init(E,S):
    • E -- 陸のマップの大きさ。
    • S -- 海のマップの大きさ。
    このプロシージャは最初にmoveTo(X,Y,A,B)が呼び出される前に一度だけ呼び出される。
    このプロシージャは戻り値を持たない。
  • 次のパラメータを持つプロシージャ moveTo(X,Y,A,B):
    • X -- 行き先の陸のマップのx座標。0≦X＜Eを仮定して良い。
    • Y -- 行き先の陸のマップのy座標。0≦Y＜Eを仮定して良い。
    • A,B -- キャラクターが使うテレポート(A,B)を表す。
    このプロシージャはQ回呼び出される。
    １回の呼び出しはキャラクターが今いる位置からテレポーター(A,B)と方向転換を複数回使って陸のマップの(X,Y)へ移動することに対応している。
    それぞれの呼び出しは、移動が可能な場合は必要なテレポーターの使用回数の最小値を、そのような移動が不可能な場合は -1 を戻り値として返す必要がある。
    また、移動が可能か不可能かに関わらず、このプロシージャが戻り値を返した後にはキャラクターは陸のマップの(X,Y)にいなければならない。

例

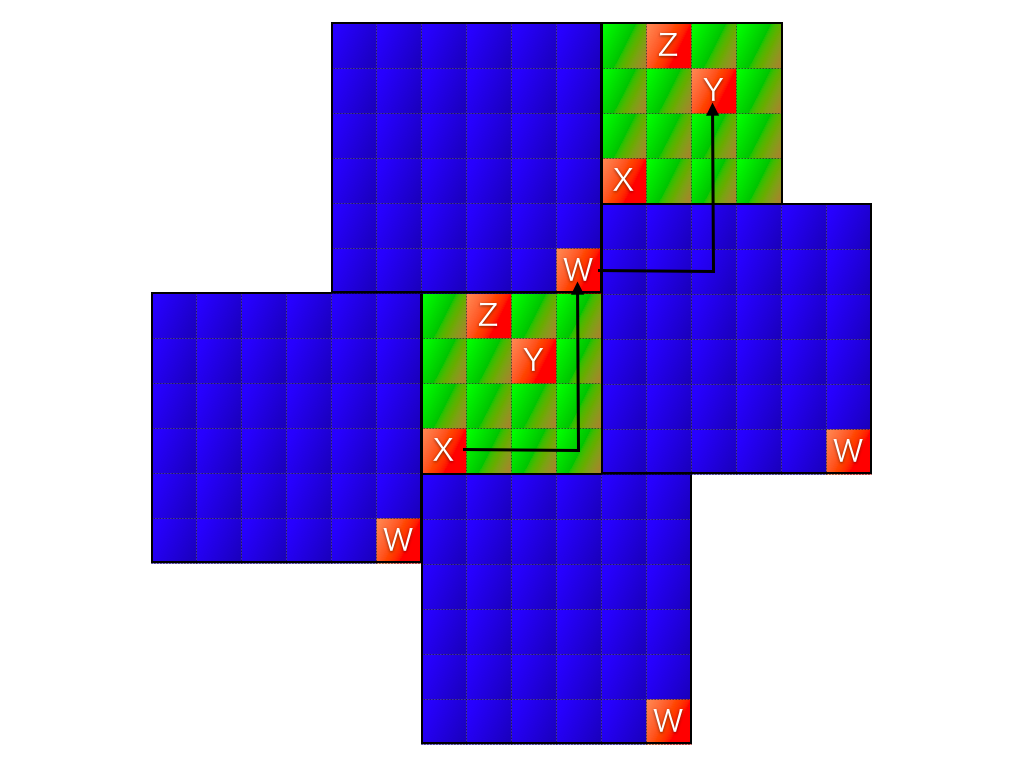
porter-fig2.png
E=4, S=6, Q=2 の場合を考える．

はじめにinit(4,6)が呼ばれ，その後moveToが2回呼ばれる．

1回目の呼び出しがmoveTo(2,2,3,4)だったとする．

ポーターが居る位置は図の地点X(0,0)であり，そこから地点Y(2,2)にテレポーター(3,4)を使って移動する．
この場合，図のように，テレポーターを1回使って地点Wに移動した後，方向転換してもう一度テレポーターを使うと地点Yに到達する．
この移動方法はテレポーターの使用回数が2回で最小となるので，正しい戻り値は2である．

その後の2回目の呼び出しがmoveTo(1,3,2,2)だったとする．

ポーターの居る位置は地点Y(2,2)であり，目的地は地点Z(1,3)である．
しかし，地点Yからテレポーター(2,2)と方向転換だけを使って地点Zに行くことはできないので．正しい戻り値は-1である．

この呼び出しのあと，ポーターは地点Zに移動する．

小課題

小課題 1 (21 点)

  • 1 ≦ E ＜ S ≦ 1 000
  • 0 ≦ A ≦ 20
  • 0 ≦ B ≦ 20
  • Q = 1

小課題 2 (27 点)

  • 1 ≦ E ＜ S ≦ 1 000
  • 0 ≦ A ≦ 1 000 000 000
  • 0 ≦ B ≦ 1 000 000 000
  • 1 ≦ Q ≦ 10

小課題 3 (52 点)

  • 1 ≦ E ＜ S ≦ 100 000
  • 0 ≦ A ≦ 1 000 000 000
  • 0 ≦ B ≦ 1 000 000 000
  • 1 ≦ Q ≦ 100 000

実装の詳細

制限

  • CPU 時間制限: 2秒
  • メモリ制限: 256 MB
    注意: スタックのサイズには決められた制限はない。スタックとして使用されたメモリは、メモリ総使用量に含まれる。

インターフェース (API)

  • 実装フォルダ: porter/ (プロトタイプ: porter.zip)
  • 競技者が実装するファイル: porter.cpp
  • 提出ファイルのインターフェース: porter.h
  • 採点プログラムのサンプル: grader.cpp
  • 採点プログラムの入力のサンプル: grader.in.1, grader.in.2, ...
    注意:採点プログラムのサンプルは次の書式の入力を読み込む。
    • 1 行目: 整数 E, S, Q が空白区切りで書かれている．Eは陸のマップの大きさ，Sは海のマップの大きさ，QはmoveToが呼ばれる回数を表す．
    • 2 行目からQ+1 行目:0 ≦ i ＜ Qに対し，i+2行には，整数 Xi, Yi, Ai, Bi が空白区切りで書かれている． これらの整数は，i+1回目のmoveToの呼び出しにおいて，目的地が(Xi, Yi)で，与えられたテレポーターが(Ai, Bi)であることを表す．
  • 採点プログラムの入力のサンプルに対して期待される出力: grader.expect.1, grader.expect.2, ...
    注意:採点プログラムのサンプルは次の書式の出力を書き出す。
    • 1行目からQ行目: 0 ≦ i ＜ Qに対して，i+1行目にはi+1回目に呼び出されたmoveToが返すべき値が書かれている．