T - Permutation 解説
by  t98slider
t98slider
解法の概要
この問題は俗に「挿入DP」と呼ばれている手法のDPを使います。この解説では以下のDPテーブルを持っています。
\[ dp[i][j]=(i番目までの位置関係を決めた時のi番目に決めた値がj番目に小さい数としたときの場合の数) \]
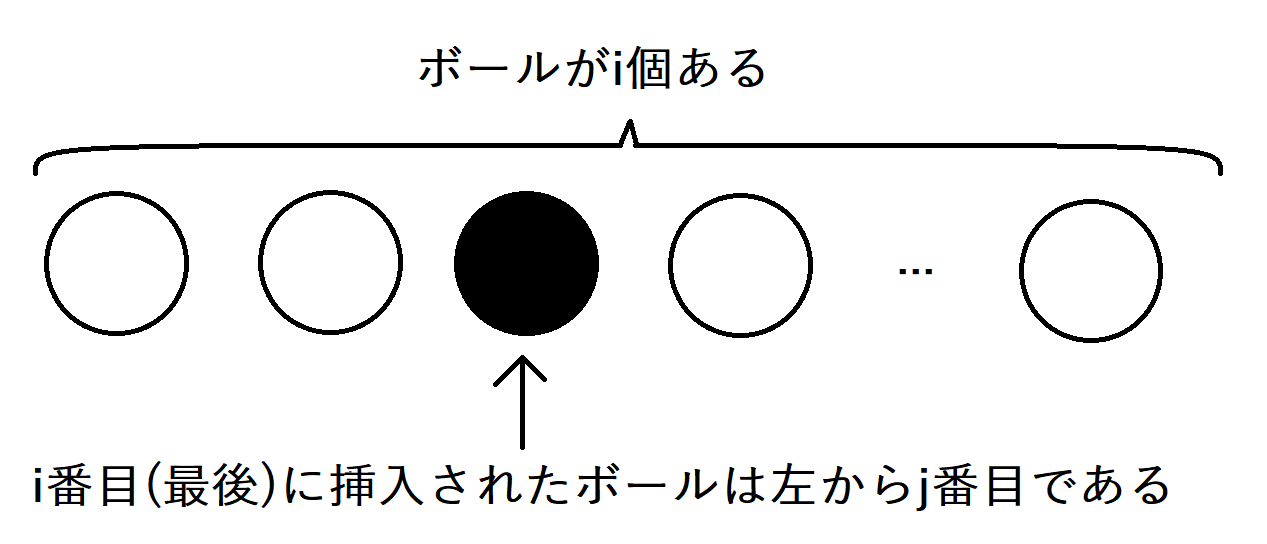
このDPテーブルの状態をボールを置いていくことに例えて図示してみると下図のようになります。
今回はこれらの状態をベースとして説明していきます。
入出力例1での説明
上の図だけではまだイメージが湧きにくいかと思いますので、入出力例1を例に遷移を見ていきましょう。入力例1
4 <><
出力例1
5
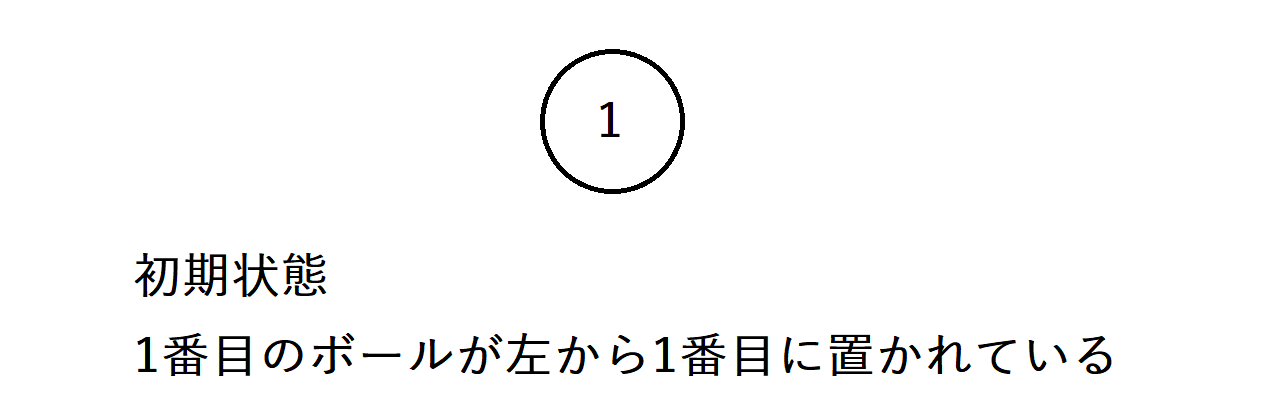
初期状態は上図のようになります。
初期状態では、ボールが1つしかないので、並び替えようがなく\(dp[1][1]=1\)となります。
ここで以下のルールを設けることとします。
・ボールに書かれている番号は、配列内の添え字に該当する。
・左に置かれているボールほど配列の要素が小さく、右に書かれているボールほど配列の要素が大きいものとする。
ボールがすべて置かれていない状態では、添え字の大小関係だけ決まっていて、その添え字に対応する番号はボールがすべて置かれるまで決まらないものとなります。
これに2~4がかかれたボールを順次挿入していくことを考えます。
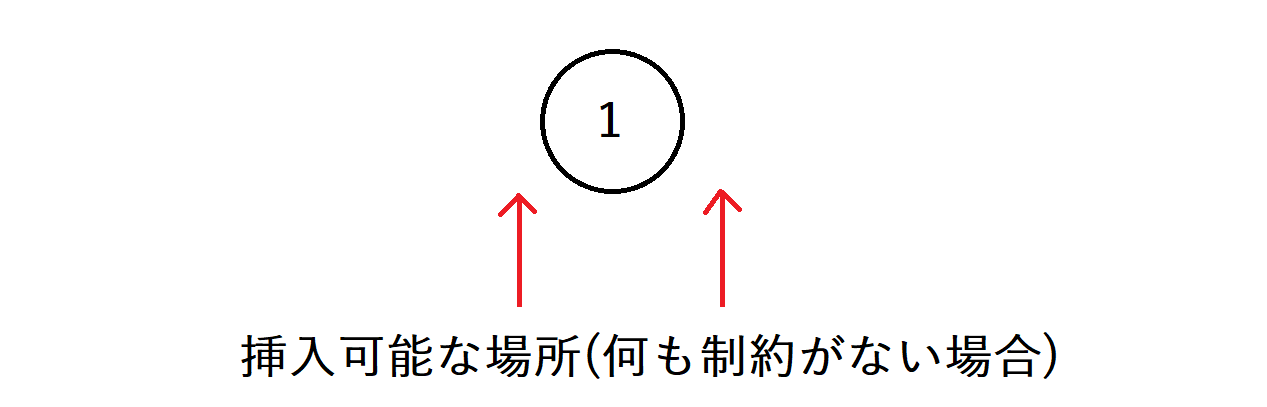
2の書かれたボールを挿入する際、何も制約がない場合は1の書かれたボールの左に挿入する場合と右に挿入する場合とで2通りの遷移があります。
しかし、文字列の1文字目は<になっており、2のボールは1のボールよりも右に置く必要があります。
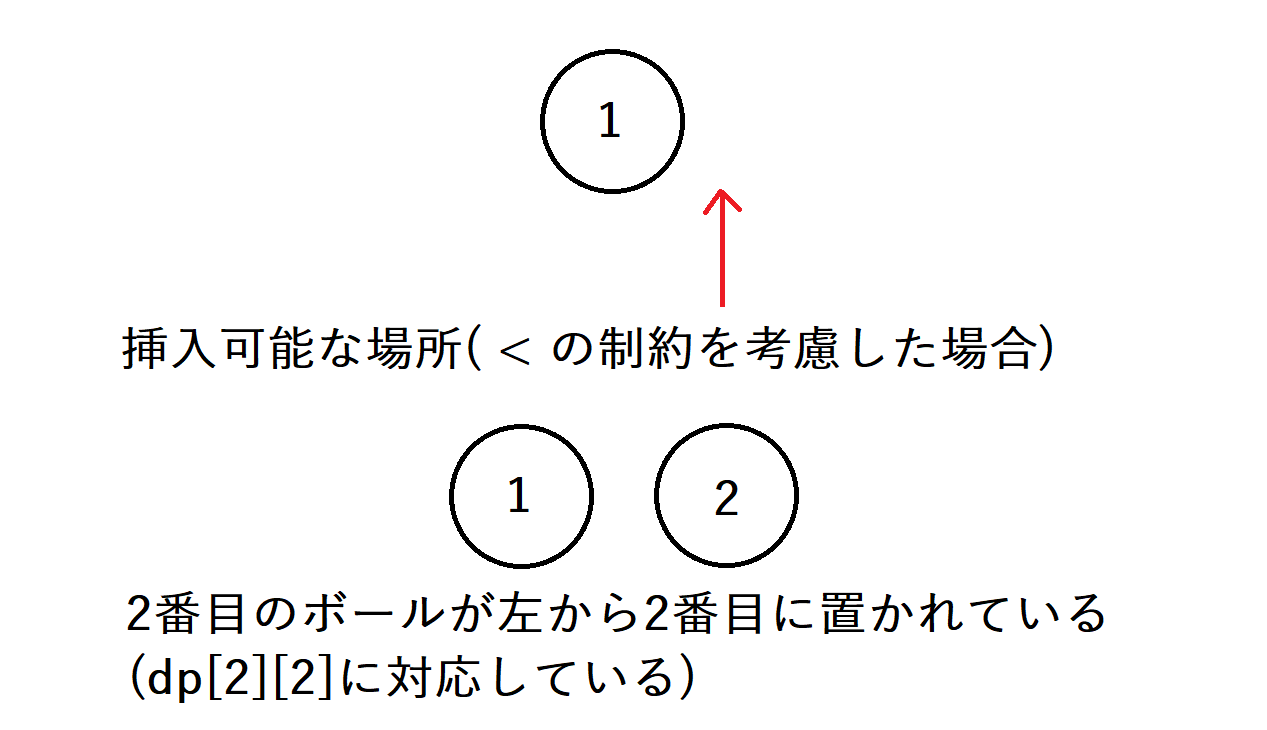
したがって、2のボールの挿入場所は1の右側へと決まります。1のボールが左から1番目に置かれている状態から2番目のボールが左から2番目に置かれている状態へ遷移したため、\(dp[2][2]+=dp[1][1]\)という遷移に対応します(+=は左辺に右辺の値を加算することを意味するものとします)。
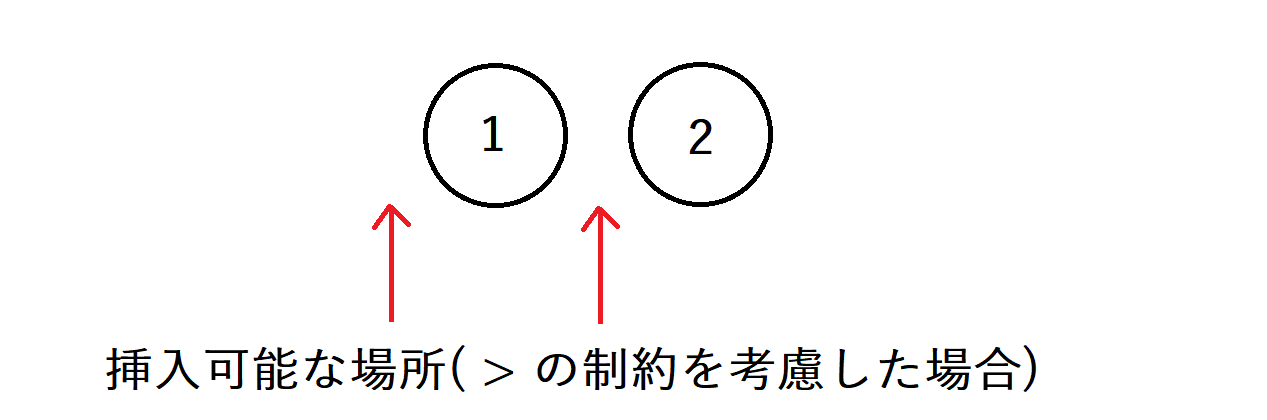
続いて、3のボールを挿入することを考えます。文字列の2文字目は>になっていますので、2のボールよりも小さい状態、すなわち2のボールより左に挿入する必要があります。これは、左から1番目と左から2番目の2つの場所があります。(3のボールが挿入されると2のボールは左から3番目へと移動します。)
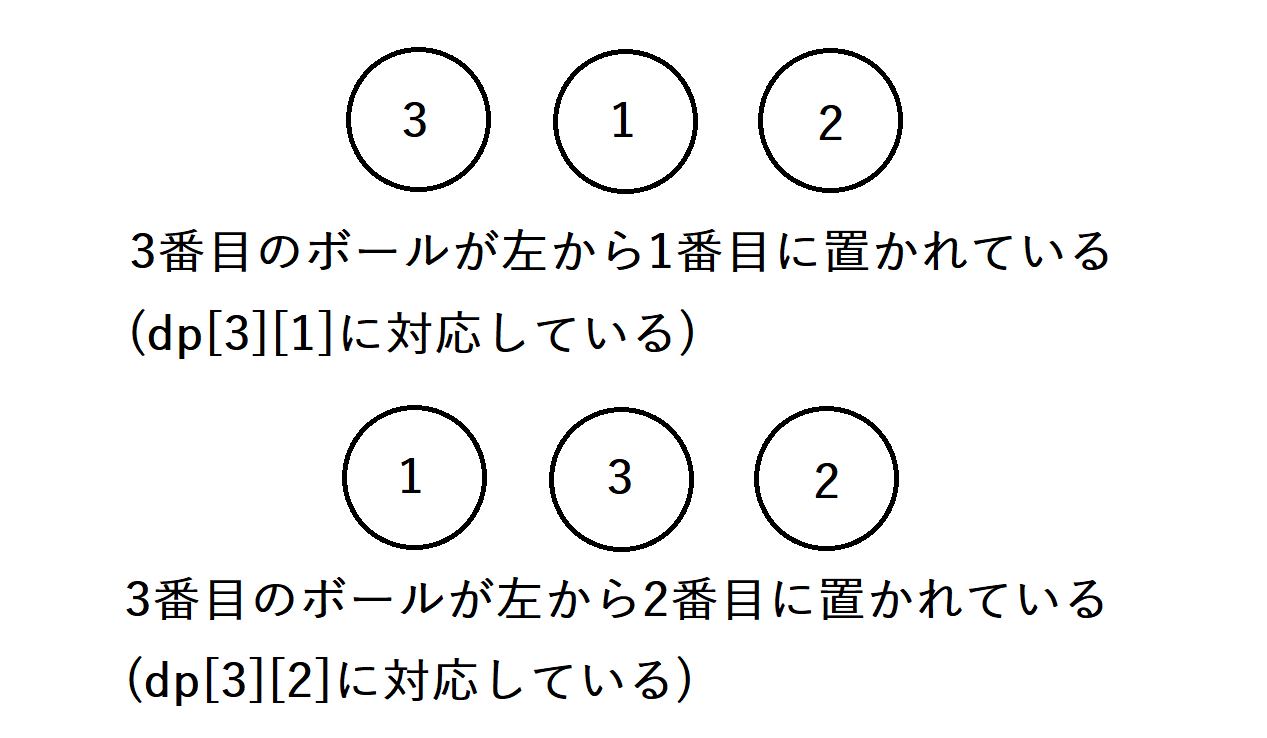
したがって、遷移先は3のボールが左から1番目に置かれた状態と3のボールが左から2番目に置かれた状態となります。この遷移は、それぞれ\(dp[3][1]+=dp[2][2]\)と\(dp[3][2]+=dp[2][2]\)に対応します。
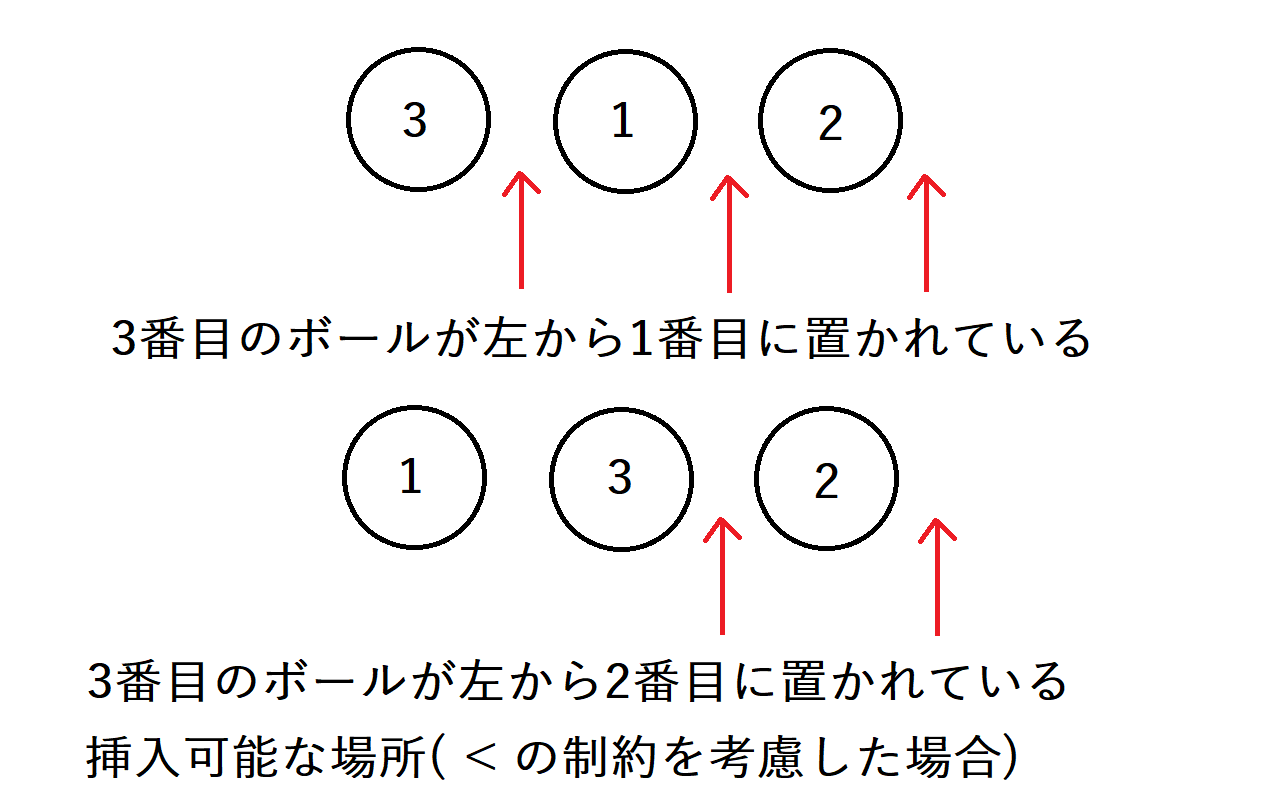
最後に、4のボールを挿入することを考えます。文字列の3文字目は<になっていますので、3のボールよりも大きい状態、すなわち3のボールよりも右に挿入する必要があります。
3のボールが左から1番目に置かれている場合は、4のボールを挿入する場所として考えられるのは、左から2、3、4番目の3箇所となります。
3のボールが左から2番目に置かれている場合は、4のボールを挿入する場所として考えられるのは、左から3、4番目の2箇所となります。
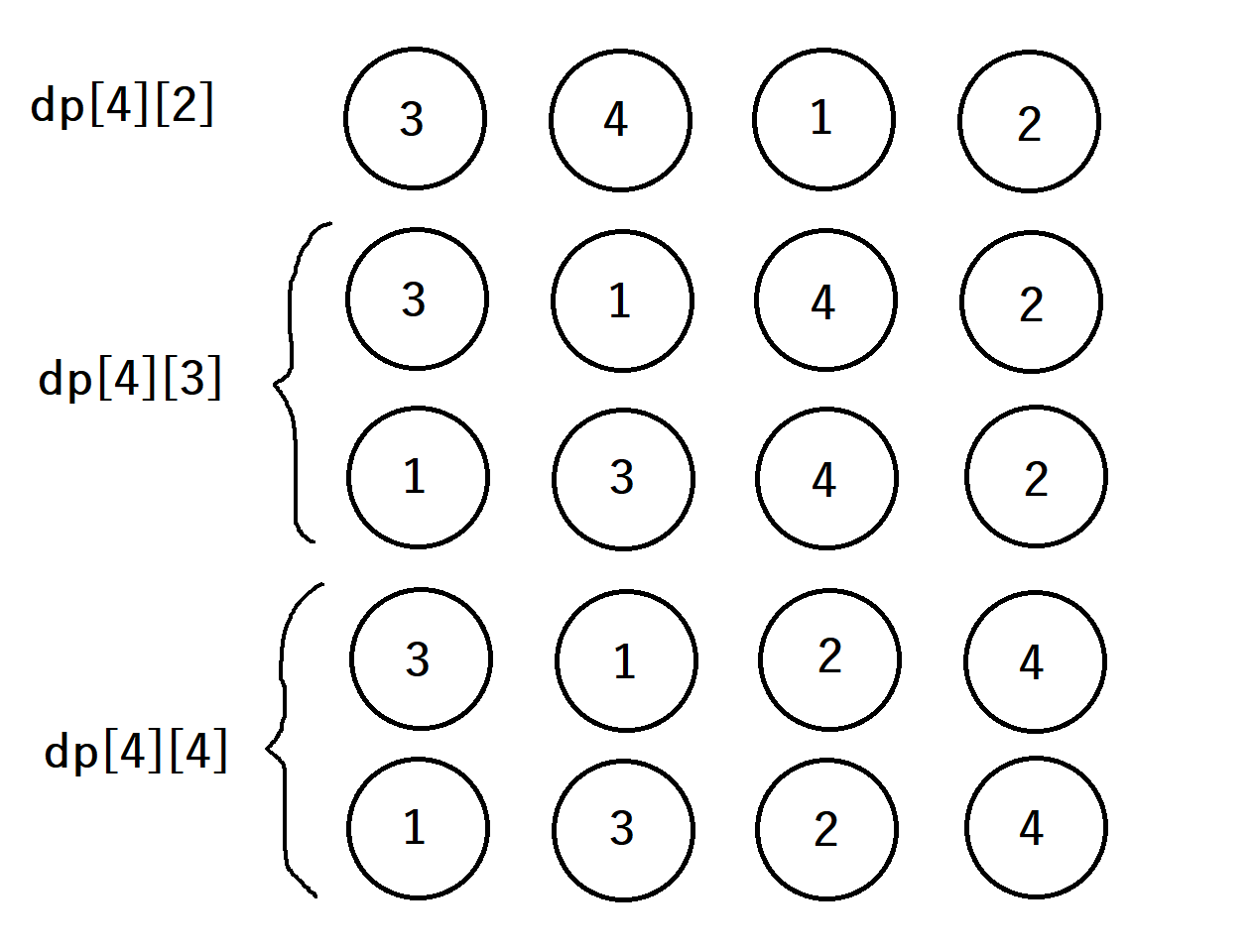
したがって、遷移先は4のボールが左から2、3、4番目に挿入されている状態の3つがあります。3のボールが左から1番目に挿入されてる状態からの遷移は
\[ ・dp[4][2]+=dp[3][1]\\ ・dp[4][3]+=dp[3][1]\\ ・dp[4][4]+=dp[3][1] \]
の3つがあります。3のボールが左から2番目に挿入されてる状態からの遷移は
\[ ・dp[4][3]+=dp[3][2]\\ ・dp[4][4]+=dp[3][2] \]
の2つがあります。この例では、\(dp[3][1]=1\)、\(dp[3][2]=1\)でしたので、
\[ dp[4][2]=dp[3][1]=1 \\ dp[4][3]=dp[3][1]+dp[3][2]=2\\ dp[4][4]=dp[3][1]+dp[3][2]=2 \]
となり、4のボールが左から2番目に挿入されている状態が1通り、左から3番目に挿入されている状態が2通り、左から4番目に挿入されている状態が2通りとなり、全部で5通りのボールの置き方が考えられることが分かりました。
なお、ボールの置き方の5通りそれぞれに対応する順列は次のようになります。
\[ ・[3,4,1,2]\to(3,4,1,2)\\ ・[3,1,4,2]\to(2,4,1,3)\\ ・[1,3,4,2]\to(1,4,2,3)\\ ・[3,1,2,4]\to(2,3,1,4)\\ ・[1,3,2,4]\to(1,3,2,4) \]
対応する順列がよく分からなかったら読んで下さい
・$[3,1,4,2]$とボール(添え字)が置かれた場合についてを例として順列を復元する方法を説明します。
便宜上配列の値を$a = (?,?,?,?)$ として、順次復元するものとします。
そこで、ボールを置いた際のルールは、
- ボールの番号は配列の添え字に該当する。
- 左に置かれているものほど小さい、右に置かれているものほど大きい
$[3,1,4,2]$では3が左から1番目に置かれているため、添え字3に対応する要素が最も小さいということになります。したがって、添え字3に該当する値は1となります。($a _ 3 = 1$に設定する。)
左から1番目まで見た時の配列:$(?,?,1,?)$
$[3,1,4,2]$では1が左から2番目に置かれているため、添え字1に対応する要素が2番目に小さいということになります。したがって、添え字1に該当する値は$2$となります。($a_1 = 2$に設定する。)
左から2番目まで見た時の配列:$(2,?,1,?)$
$[3,1,4,2]$では4が左から3番目に置かれているため、添え字4に対応する要素が3番目に小さいということになります。したがって、添え字4に該当する値は$3$となります。($a_4 = 3$に設定する。)
左から3番目まで見た時の配列:$(2,?,1,3)$
$[3,1,4,2]$では2が左から4番目に置かれているため、添え字2に対応する要素が4番目に小さいということになります。したがって、添え字2に該当する値は$4$となります。($a_2 = 4$ に設定する。)
左から4番目まで見た時の配列:$(2,4,1,3)$
したがって、ボール(添え字)の置き方$[3, 1, 4, 2]$に対応する順列が$(2, 4, 1, 3)$であることが分かります。
逆置換と自己逆置換について(どうでもいい話題)
長さ$N$の順列 $ q = (q_1, q_2, \cdots, q_N) $について、$p_{q_{i}}=i$を満たすように定めた順列 $ p $ は $ q $ についての逆置換(または逆順列) ( inverse permutation ) と呼ばれます。$p_{k}$ には順列$q$において $ k $ がどこにあるかどういう情報が保持されています。実は、 $ p $ は $ q $ の逆置換である他に $ q $ も $ p $ の逆置換であるため順列について2回逆置換をとると元に戻る性質があります。したがって、ここで紹介した挿入DPでは逆置換空間での並び替えを考えていることに相当します。(逆置換には、他にも順列とその逆置換で転倒数が一致するといった性質などもあります。)
また、上の例で見たように $ [3, 4, 1, 2] \to (3, 4, 1, 2) $ のように順列と逆置換が一致する、すなわち$p = q$となるものがあります。このような順列$p$、$q$は自己逆置換(または自己逆順列) ( self-inverse permutation ) と呼ばれます。長さ$N$の順列についての自己逆置換の数$a_N$は以下の漸化式で表される数列の第 $ N $ 項に相当します。
- $a_1 = 1$
- $a_2 = 2$
- $a_i = a_{i-1} + (i - 1)\,a_{i-2}$
この漸化式を使う問題がCodeforcesで出題されていますので、興味を持っていただけた方は挑戦してみてください。 問題へのURL
一般化
ここまでの話を一般化してみましょう。初期状態については、入出力例と同じくボールが1つしかないので並び替えようがなく、\(dp[1][1]=1\)となります。以下、遷移について説明します。\(i\)文字目が<の場合
\(i\)文字目の時点ではボールが\(i\)個置かれています。\(i\)の書かれたボールを左から\(j\)番目に挿入したとして、この状態から\(i+1\)の書かれたボールを挿入することを考えます。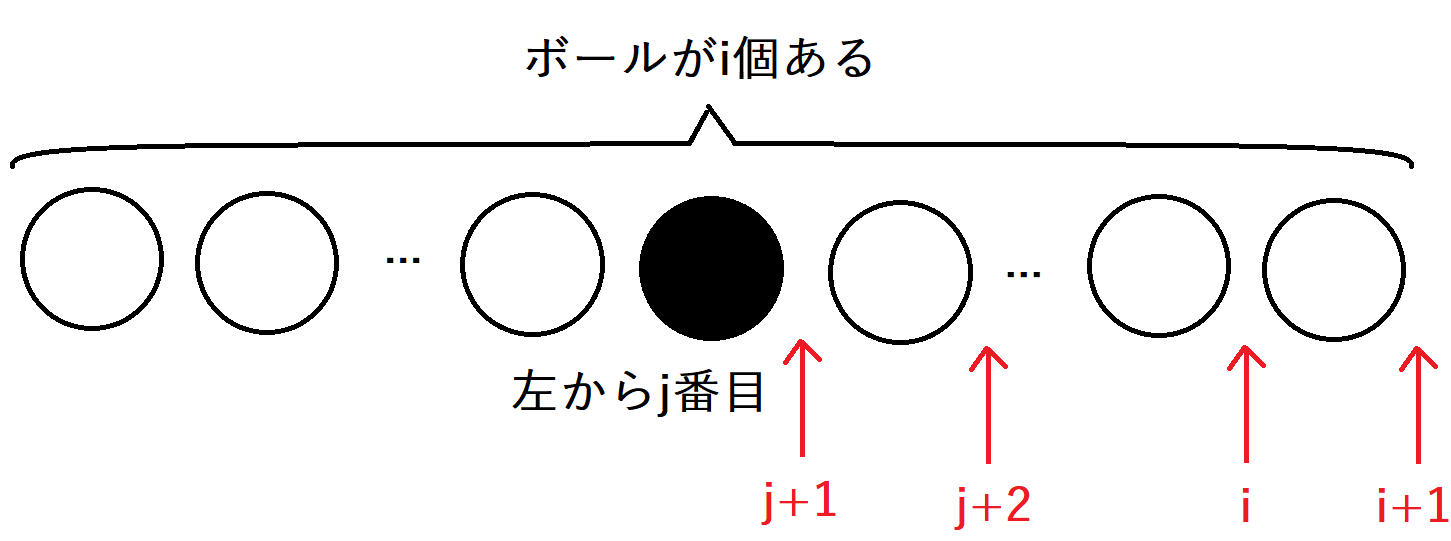
\(i\)のボールが左から\(j\)番目に置かれている場合、\(i+1\)のボールを挿入する場所として可能なのは、文字列が
<であることから\(i\)のボールよりも大きい状態、すなわち\(j\)の右側である\(j+1\)、\(j+2\)、\(j+3\)、\(\cdots\)、\(i-1\)、\(i\)、\(i+1\)
となります。すなわち、\(k \) を \( j+1 \leq k \leq i+1\)の範囲の整数として、\(dp[i+1][k]+=dp[i][j]\)が成り立ちます。しかし、このままでは状態が\(O(N^{2})\)、遷移が\(O(N)\)となり、全体で\(O(N^{3})\)の計算量となるため、実行時間に間に合いません。
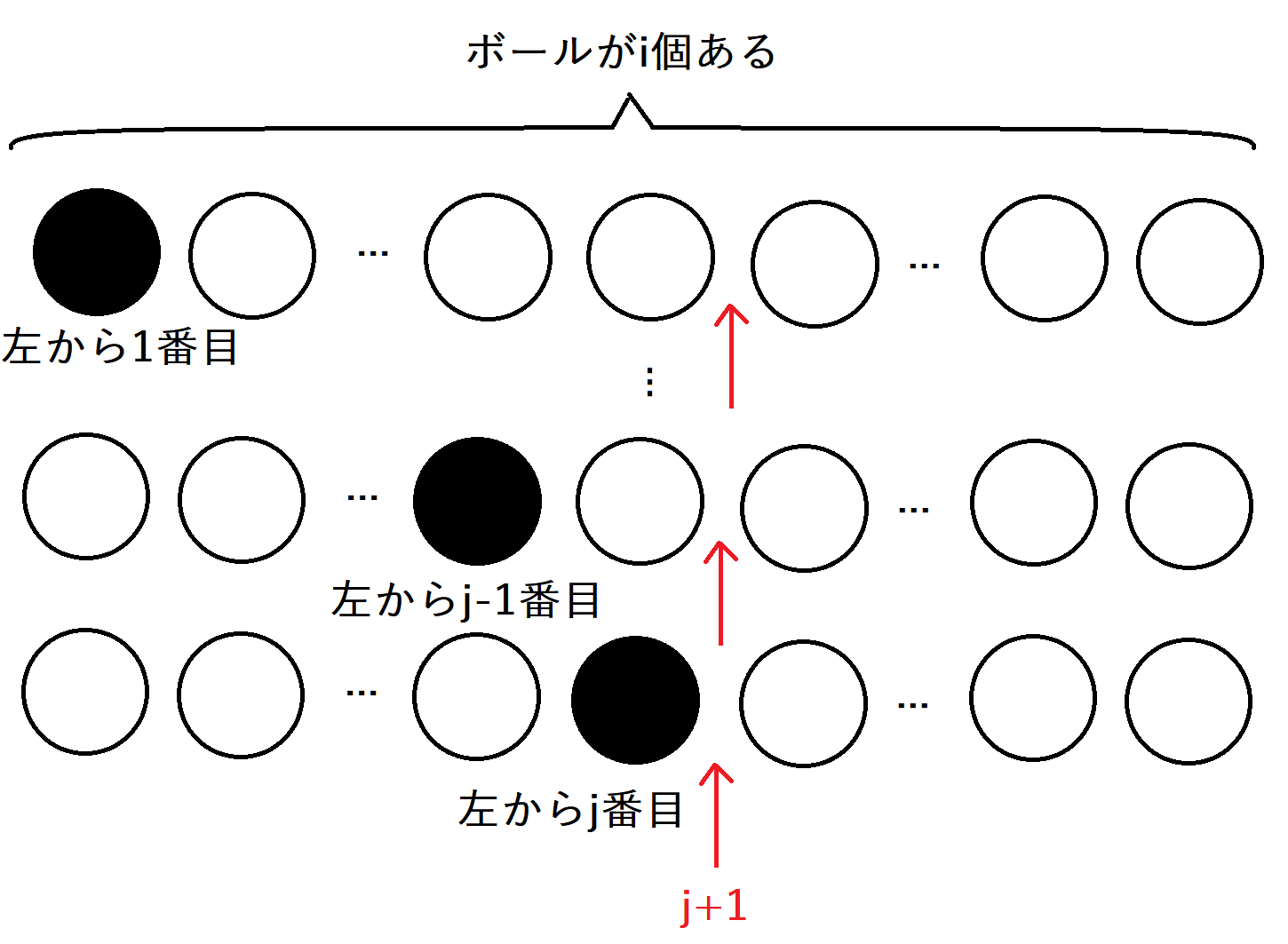
そこで、累積和による高速化を考えます。ここでは、ひとまず\(i+1\)のかかれたボールを左から\(j+1\)番目に挿入するものとして着目します(配るDPから貰うDPへと視点を変えたことになります)。このようにすると、\(i\)のかかれたボールが左から\(j+1\)よりも小さい状態はすべて\(i+1\)のボールを左から\(j+1\)番目に挿入することができることが分かるかと思います。すなわち、\(dp[i][1]\)、\(dp[i][2]\)、\(\cdots\)、\(dp[i][j-1]\)、\(dp[i][j]\)が\(dp[i+1][j+1]\)に遷移できます。式で表すと、
\[dp[i+1][j+1]=\sum_{k=1}^{j}dp[i][k]\]
となります。したがって、\(dp[i]\)の累積和をもっておくことで\(dp[i+1]\)への遷移は\(O(1)\)となり、計算量を\(O(N^{2})\)まで落とすことができます。\(i\)文字目が>の場合
\(i\) の書かれたボールを左から\(j\)番目に挿入したとして、この状態から\(i+1\) の書かれたボールを挿入することを考えます。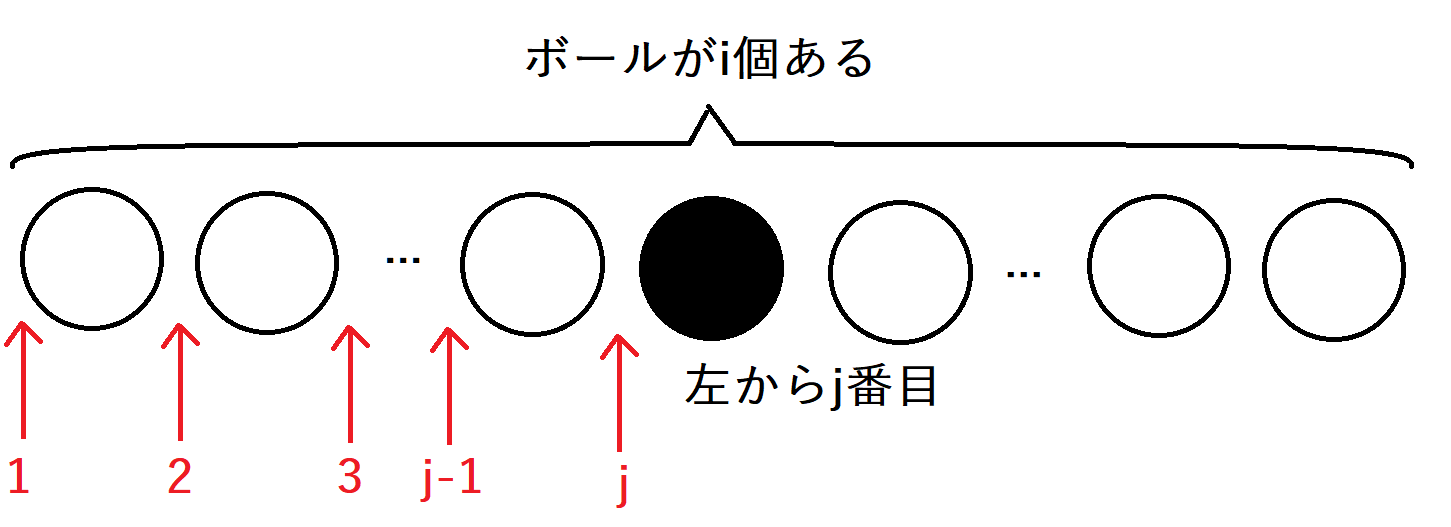
\(i\)のボールが左から\(j\)番目に置かれている場合、\(i+1\)のボールを挿入する場所として可能なのは、文字列が
>であることから\(i\)のボールよりも小さい状態、すなわち\(j\)の左側である\(1\)、\(2\)、\(\cdots\)、\(j-2\)、\(j-1\)、\(j\)
となります。すなわち、\(k \) を \( 1 \leq k \leq j\)の範囲の整数として、\(dp[i+1][k]+=dp[i][j]\)が成り立ちます。しかし、このままでは状態が\(O(N^{2})\)、遷移が\(O(N)\)となり、全体で\(O(N^{3})\)の計算量となるため、実行時間に間に合いません。
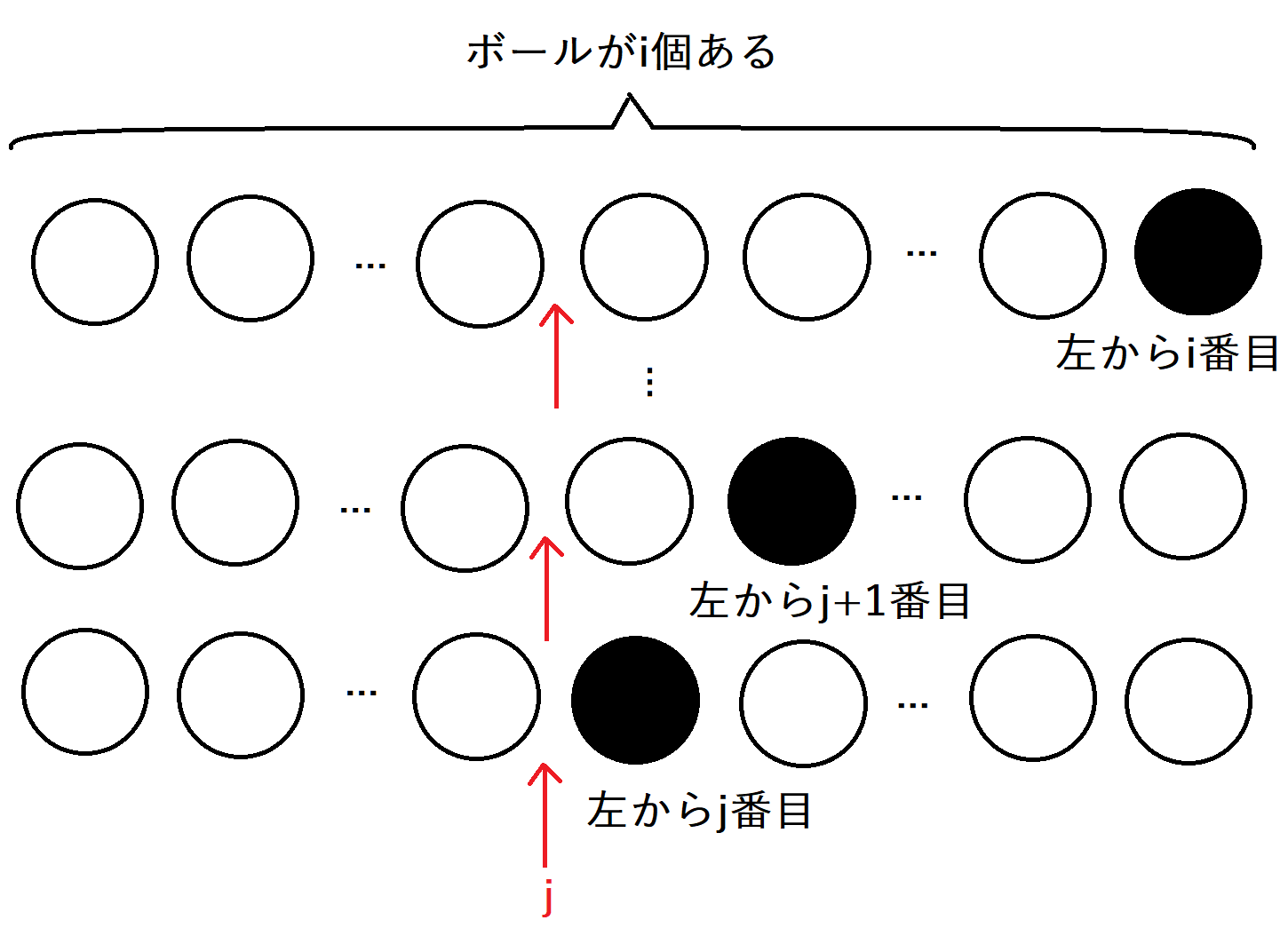
そこで、累積和による高速化を考えます。ここでは、ひとまず\(i+1\)のかかれたボールを左から\(j\)番目に挿入するものとして着目します。このようにすると、\(i\)のかかれたボールが左から\(j\)番目よりも大きい状態はすべて\(i+1\)のボールを左から\(j\)番目に挿入することができることが分かるかと思います。すなわち、\(dp[i][j]\)、\(dp[i][j+1]\)、\(\cdots\)、\(dp[i][i-1]\)、\(dp[i][i]\)が\(dp[i+1][j]\)に遷移できます。式で表すと、
\[dp[i+1][j]=\sum_{k=j}^{i}dp[i][k]\]
となります。したがって、\(dp[i]\)の累積和をもっておくことで\(dp[i+1]\)への遷移は\(O(1)\)となり、計算量を\(O(N^{2})\)まで落とすことができます。まとめ
以上のことをまとめると以下のようになります。初期状態
\(dp[1][1]=1\)遷移
\(i\)文字目が<のとき
\(dp[i+1][j+1]=\sum\limits_{k=1}^{j}dp[i][k]\)\(i\)文字目が
>のとき
\(dp[i+1][j]=\sum\limits_{k=j}^{i}dp[i][k]\)
実装例 (C++ with ACL)
#include <bits/stdc++.h>
#include <atcoder/all>
using namespace std;
using mint = atcoder::modint1000000007;
int main(){
int n;
string s;
cin >> n >> s;
mint dp[n + 1][n + 1];
dp[1][1] = 1;
for(int i = 1; i < n; i++ ){
if(s[i - 1] == '<'){
mint sumv;
for(int j = 1; j <= i; j++){
sumv += dp[i][j];
dp[i + 1][j + 1] += sumv;
}
}else{
mint sumv;
for(int j = i; j >= 1; j--){
sumv += dp[i][j];
dp[i + 1][j] += sumv;
}
}
}
mint ans;
for(int i = 1; i <= n; i++)ans += dp[n][i];
cout << ans.val() << endl;
}
別の実装例
配るDPのまま考える
俗にいもす法と呼ばれている累積和に対する区間加算を行うテクニックを用いることによって配るDPのまま遷移を考えることも可能です。実装例 (C++ with ACL)
#include <bits/stdc++.h>
#include <atcoder/all>
using namespace std;
using mint = atcoder::modint1000000007;
int main(){
int N;
string s;
cin >> N >> s;
mint dp[N + 1][N + 1];
dp[0][0] = 1;
s += '?';
for(int i = 0; i < N; i++){
for(int j = 0; j <= i; j++){
dp[i][j + 1] += dp[i][j];
if(s[i] == '<'){
dp[i + 1][j + 1] += dp[i][j];
dp[i + 1][i + 2] -= dp[i][j];
}else{
dp[i + 1][0] += dp[i][j];
dp[i + 1][j + 1] -= dp[i][j];
}
}
}
cout << accumulate(dp[N - 1], dp[N - 1] + N, mint(0)).val() << endl;
}
配列の使いまわし(1次元配列で解く)
この問題は、簡単に言ってしまえば、<が来たら左から右に累積和>が来たら右から左に累積和
<と>の配分によって累積和が適用される範囲が変化することになるため少々難しいです。そこで、両端キューのようなデータ構造を用いることによって、累積和の適用される範囲を深く考えずに遷移させることが可能です。
実装例 (C++ with ACL)
#include <bits/stdc++.h>
#include <atcoder/all>
using namespace std;
using mint = atcoder::modint1000000007;
int main(){
int N;
string s;
cin >> N >> s;
deque<mint> dp(1, 1);
for(int i = 0; i + 1 < N; i++){
s[i] == '<' ? dp.push_front(0) : dp.push_back(0);
for(int j = 0; j <= i; j++){
s[i] == '<' ? dp[j + 1] += dp[j] : dp.rbegin()[j + 1] += dp.rbegin()[j];
}
}
cout << accumulate(dp.begin(), dp.end(), mint(0)).val() << endl;
}
類題
類題のページABCにほとんど同じ解法で解ける問題があるのでぜひ挑戦してみてください。ネタバレが嫌な方もいらっしゃるかと思いますので問題名はあえて伏せてあります。
投稿日時:
最終更新:
