 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 700 点
問題文
半径 R のウェーハを水平方向に等間隔で切って N 分割することにしました。ウェーハとは、ある部品を作るのに使われる薄い円盤状の物体です。
ウェーハを等間隔で N 分割するためのカットラインと呼ばれる線が N-1 本あります。 カットラインには上から順に 1 ~ N-1 の番号が付いています。 また、下図に示されるように 0 以下や N 以上の番号のカットラインも便宜上存在することにします。
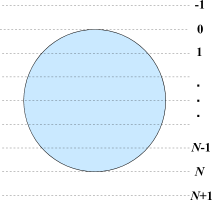
ウェーハを N 分割するためにデュアルカットという手法を用いることにしました。
デュアルカットでは、カットラインに対してカットという操作を何度か行います。 1 回のカットでは、2 枚の刃を使用して 2 本のカットラインを同時に切断します。 切断に用いる機械の制約上、2 本のカットラインは一定以上離れている必要があります。 より正確には、同時に切断する 2 本のカットラインの番号をそれぞれ i,j (i<j) とすると、i+M ≦ j を満たしていなければなりません。 この問題では、同じカットラインを 2 回以上切断したり、0 以下や N 以上の番号のカットラインを切断したりしても構いません。
i 番と j 番のカットラインを同時に切るときのカット長は、2 本のカットラインの長さのうちの長い方の長さで表されます。 ここで i \, (1 ≦ i ≦ N-1) 番のカットラインの長さとは i 番のカットラインで示される直線とウェーハの共通部分の線分の長さであり、それ以外の 0 番や N 番などのカットラインの長さは 0 です。
機械の動作の具体例を示します。N=6, \, M=3 のときに i=2, \, j=5 として機械を稼働させると、下図(左)のように 2 番と 5 番のカットラインがカットされます。このときのカット長は 2 番のカットラインの方が 5 番のカットラインより長いため、2 番のカットラインの長さとなります。カットラインの長さは図中で赤色の実線で示されています。 ここで、下図(右)のような i=3,\,j=5 といった操作は i+M ≦ j を満たさないため、行うことができないことに注意してください。
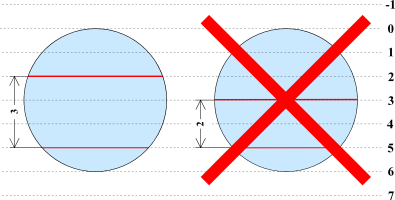
1 ~ N-1 番のカットラインそれぞれ 1 回以上切断するとウェーハを N 分割することが出来ます。 うまく機械を操作することで、ウェーハを N 分割するときのカット長の総和を最小化したいです。 カット長の総和の最小値を求めてください。
制約
- 1 ≦ R ≦ 10^{3}
- 2 ≦ N ≦ 10^{3}
- 1 ≦ M ≦ N - 1
- R は整数
部分点
- M=1 を満たすデータセットに正解した場合は、300 点が与えられる。
- 追加制約のないデータセットに正解した場合は、上記とは別に 400 点が与えられる。
入力
入力は以下の形式で標準入力から与えられる。
R N M
出力
答えを 1 行で出力せよ。絶対誤差、あるいは相対誤差が 10^{-6} 以下であれば許容される。
入力例 1
100 4 1
出力例 1
373.2050807569
以下のようにカットするのが最適な操作の手順の 1 つです。
- 1 番と 2 番のカットラインを切断する
- 0 番と 3 番のカットラインを切断する
このケースは部分点の制約を満たします。
入力例 2
100 4 3
出力例 2
546.4101615138
以下のようにカットするのが最適な操作の手順の 1 つです。
- 0 番と 3 番のカットラインを切断する
- 1 番と 4 番のカットラインを切断する
- 2 番と 5 番のカットラインを切断する
M が入力例 1 と異なり 3 であるため、1 番と 2 番を同時に切断することや、1 番と 3 番を同時に切断することなどは、機械の制約上指定できないことに注意してください。
入力例 3
43 65 12
出力例 3
2208.8155789165
入力例 4
1000 1000 999
出力例 4
1570743.7385010704