まず、元の問題を最小費用流の問題として定式化しましょう。

\(i\) 番目のアトラクションに対応する頂点 \(i\) と、それに加えて \(4\) つの頂点 \(v_A,v_B,s,f\) を用意した画像のようなグラフを考えます。
( 各辺は 容量/単位流量あたりのコストを表します )

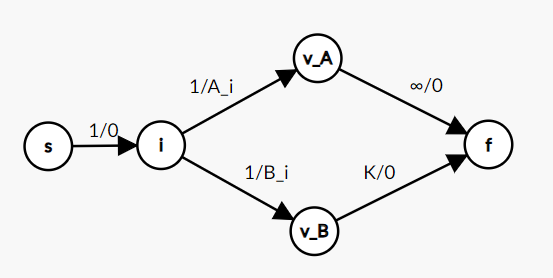
• \(s \rightarrow i \rightarrow v_A \rightarrow f\) と流すことは「\(i\) 番目のアトラクションに通常通り搭乗」することに対応します。
• \(s \rightarrow i \rightarrow v_B \rightarrow f\) と流すことは「\(i\) 番目のアトラクションにファストパスを使って搭乗」することに対応します。

このとき、 \(s\) から \(t\) へ流量 \(k\) を流す際の最小コスト \(c\) が \(c \le T\) であれば答えは \(k\) 以上、そうでなければ答えは \(k\) 未満です。

これで多項式時間でこの問題を解くことはできましたが、まだ速度が足りません。
実は、この最小費用流による解法を観察することでこの問題に正解できます。どのようにすればよいでしょうか？

最小費用流の解法のひとつである、最短路反復を観察します。
(最小費用流 / 最短路反復 に関しては、インターネット上に資料が多数あります。 参考1 参考2 参考3 )
流量 \(F\) を流す際に必要なコストを \(F=1,2,\dots,N\) について順々に求めていくことを考えます。

流量を \(1\) 増やすと起こりうる挙動は、実は以下の \(3\) 通りです。

1. 何らかの \(i\) に対し、 \(s \rightarrow i \rightarrow v_A \rightarrow f\) にフローを \(1\) 流す。
   • この際、発生するコストは \(A_i\) です。
2. 何らかの \(i\) に対し、 \(s \rightarrow i \rightarrow v_B \rightarrow f\) にフローを \(1\) 流す。
   • この際、発生するコストは \(B_i\) です。
3. 何らかの \(i,j\) ( \(i \neq j\) ) に対し、 \(s \rightarrow i \rightarrow v_B \Rightarrow j \rightarrow v_A \rightarrow f\) にフローを \(1\) 流す。
   • 但し、 \(\Rightarrow\) は以前のフローによって張られた逆辺を表します。
   • この際、発生するコストは \(B_i+(A_j-B_j)\) です。

流量を \(x \rightarrow x+1\) に増やす際の挙動を調べましょう。

• もし、 \(x < K\) であれば制約 \(A_i \ge B_i\) より必ずファストパスを使うべきです。なので、上記の挙動のうち 2. のみ発生します。
  
• もし、 \(x \ge K\) であれば既に \(v_B \rightarrow f\) に使える流量は残っていません。なので、上記の挙動のうち 1. と 3. のみ発生します。(この両挙動のうち追加で発生するコストが小さいものを採用すればよいです)

ここで、以下のデータ構造を使うことでこの最小費用流をシミュレートできます。

• \(A_i\) の昇順に取り出す priority_queue
• \(B_i\) の昇順に取り出す priority_queue
  • この \(2\) つは \(s \rightarrow i\) を採用していないものを管理しておきます。
• \(A_i-B_i\) の昇順に取り出す priority_queue
  • これは \(i \rightarrow v_B\) を採用しているものを管理しておきます。

これにより、この問題を時間計算量 \(O(N \log N)\) で解くことができました。詳細は実装例も参照してください。

実装例 (C++)

#include<bits/stdc++.h>

using namespace std;

using pl=pair<long long,long long>;
using pq=priority_queue<pl,vector<pl>,greater<pl>>;

long long solve(long long n,long long k,long long t,vector<long long> &a,vector<long long> &b){
  pq qa,qb,qmv;
  for(long long i=0;i<n;i++){
    qa.push({a[i],i});
    qb.push({b[i],i});
  }

  pl vd={2e18,2e18};
  qa.push(vd);
  qb.push(vd);
  qmv.push(vd);
  vector<long long> used(n,0);
  long long clk=0;

  for(long long tr=1;tr<=n;tr++){
    while(qa.top()!=vd){
      if(used[qa.top().second]){qa.pop();}
      else{break;}
    }
    while(qb.top()!=vd){
      if(used[qb.top().second]){qb.pop();}
      else{break;}
    }
    long long ca=qa.top().first;
    long long cb=qb.top().first;
    long long cmv=qb.top().first+qmv.top().first;

    if(k>0){
      k--;
      long long tg=qb.top().second;
      clk+=cb;
      used[tg]=1;
      qb.pop();
      qmv.push({a[tg]-b[tg],tg});
    }
    else if(ca<=cmv){
      long long tg=qa.top().second;
      clk+=ca;
      used[tg]=1;
      qa.pop();
    }
    else{
      long long tg=qb.top().second;
      clk+=cmv;
      used[tg]=1;
      qb.pop();
      qmv.pop();
      qmv.push({a[tg]-b[tg],tg});
    }
    
    if(clk>t){return tr-1;}
  }
  return n;
}

int main(){
  long long n,k,t;
  cin >> n >> k >> t;
  vector<long long> a(n),b(n);
  for(long long i=0;i<n;i++){
    cin >> a[i] >> b[i];
  }
  cout << solve(n,k,t,a,b) << "\n";
  return 0;
}