E - ab文字列 Editorial
by  t98slider
t98slider
解法の概要
フィボナッチ探索(黄金分割探索)のような探索幅で再帰的に探索幅を狭めていき、\(F_{p,q}\) における \(q\) の値を決定する解法です。解法
問題の漸化式は以下のようになっていました。- \(F_{1,0} = \)
b - \(F_{2,0} = \)
a - \(n \geq 3\) かつ \(0 \leq k < 2^{n-2}\) かつ \(k\) が偶数のとき、\(F_{n,k} = F_{n-1,{\rm floor}(k/2)} + F_{n-2,{\rm floor}(k/4)}\)
- \(n \geq3 \) かつ \(0 \leq k < 2^{n-2}\) かつ \(k\) が奇数のとき、\(F_{n,k} = F_{n-2,{\rm floor}(k/4)} + F_{n-1,{\rm floor}(k/2)}\)
まず、\(p\)については、文字数から決定することができます。\(|F_{n}|\)を文字数とすると、文字数は、
- $|F_{1}| = 1$
- $|F_{2}| = 1$
- $|F_{n}| = |F_{n - 1}| + |F_{n - 2}|$
という漸化式に従っているため、フィボナッチ数列の何項目が文字列\(s\)の長さに一致するかを調べることで\(p\)について解くことができます。(この際、\(|F_{1}| = |F_{2}| = 1\)であることに注意してください。)
この問題では、\(|s| \leq 10 ^{4}\)の制約で、フィボナッチ数列の第21項が\({\rm fib}[21] = 10946\)でしたので、フィボナッチ数列を21項目まで列挙しておけば十分でしょう。この解説では、以下フィボナッチ数列の第\(N\)項目を\({\rm fib}[N]\)と表記することとします。
続いて、\(q\)について考えます。ここで、フィボナッチ数列の第\(N\)項目の長さを持つ文字列(以下、単に第\(N\)項に対する文字列と呼ぶこととします。)を\(s_{N}\)として、\(N \geq 3\)を仮定すると、
- 偶数のとき:\(s_{N} = s_{N - 1} + s_{N - 2}\)
- 奇数のとき:\(s_{N} = s_{N - 2} + s_{N - 1}\)
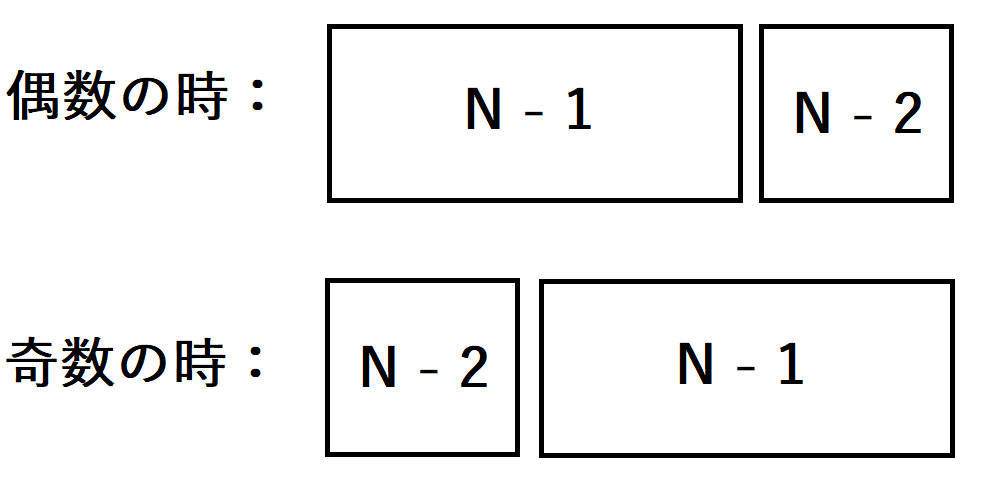
ここで、\(N-1\)項目に対する文字列\(s_{N - 1}\)に対応する\(k\)の値が\(k_{N-1}\)であったとすると、\(N\)項目に対する文字列\(s_{N }\)に対応する\(k_{N}\)の値は
- 偶数のとき:\(k_{N} = 2 k_{N-1}\)
- 奇数のとき:\(k_{N} = 2 k_{N-1} + 1\)
よって、この問題はフィボナッチ数列の第\(N\)項目\({\rm fib}[N]\)に等しい長さの半開区間\([L, R)\)に対して、前の区間\([L,L+{\rm fib}[N-1] )\)を \(N-1\) の区間として選ぶか、後ろの区間\([R - {\rm fib} [N-1],R)\)を \(N-1\) の区間として選ぶかの2択を繰り返していく問題と言い換えられます。以下、この解説では、奇数の時の\(N-1\)の区間を後ろに選ぶ\(s_{N} = s_{N - 2} + s_{N - 1}\)の状態を反転状態と呼ぶこととします。また、フィボナッチ数列の第\(N\)項目\({\rm fib}[N]\)に等しい長さの半開区間\([L, R)\)を単に\(N\)の区間と呼ぶこととします。
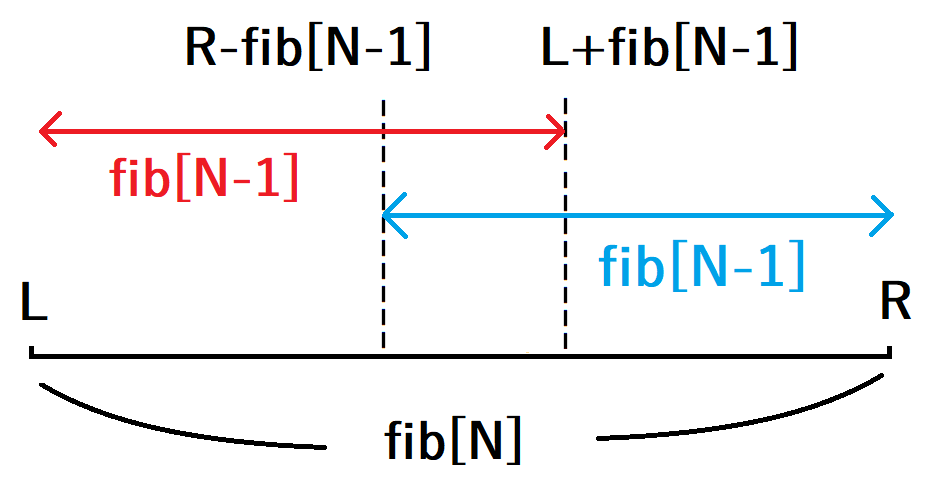
余談ですが、漸化式には\(N-2\)もあるので、\(N\)の区間から\(N-2\)の区間を選択してはいけないのかと考える方もいらっしゃるかと思いますが、\({\rm floor}(k_{N} / 4)\)の性質から、
- 偶数のとき:\(4 k _{N-2}\)と\(4 k _{N-2} +2\)
- 奇数のとき:\(4 k _{N-2} + 1\)と \(4 k _{N-2} +3\)
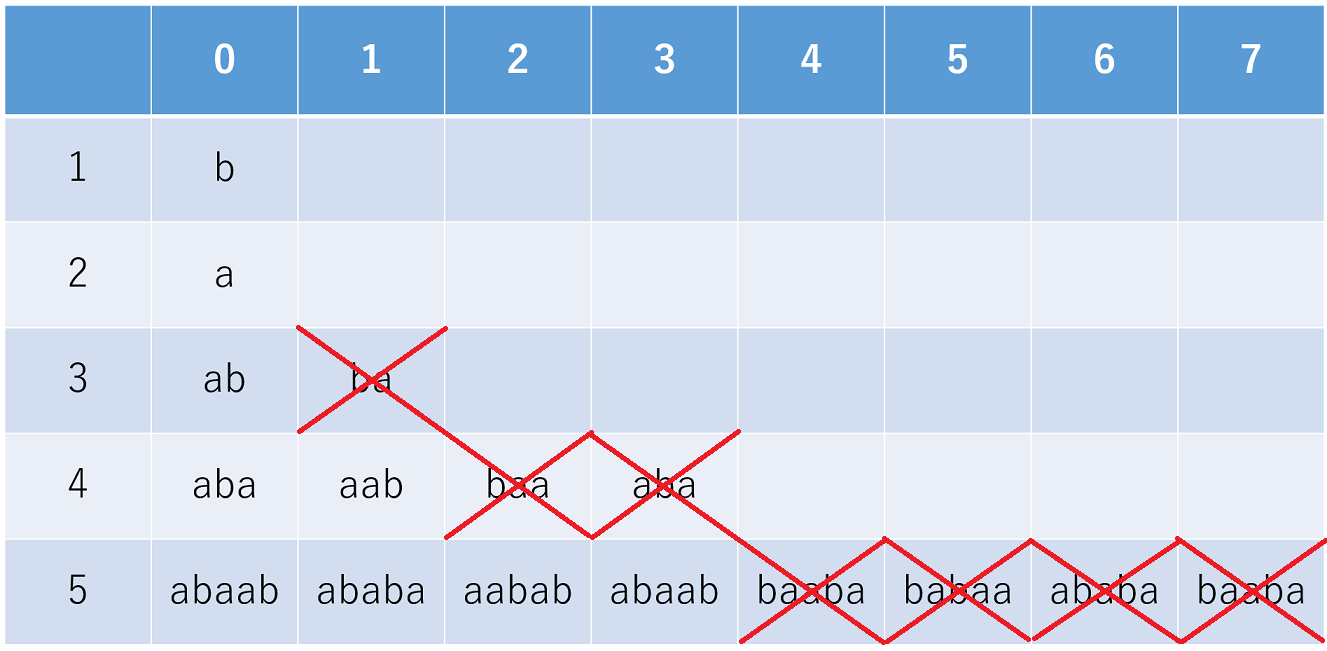
続いて、\(N\)の区間から\(N-1\)の区間を選ぶ際、前の区間と後ろの区間どちらを採用するのが最適かについて考えます。具体例をいくつか挙げるため、表1に\(N \leq 5\) 以下の文字列について列挙しておきました。

\(N\)に対する文字列\(s_{N}\)について
- \(s_{N} = s_{N - 1} + s_{N - 2}\)
- \(s_{N} = s_{N - 2} + s_{N - 1}\)
- \(s_{N} = s_{N - 3} + s_{N - 2} + s_{N - 2}\)
- \(s_{N} = s_{N - 2} + s_{N - 3} + s_{N - 2}\)
- \(s_{N} = s_{N - 2} + s_{N - 2} + s_{N - 3}\)
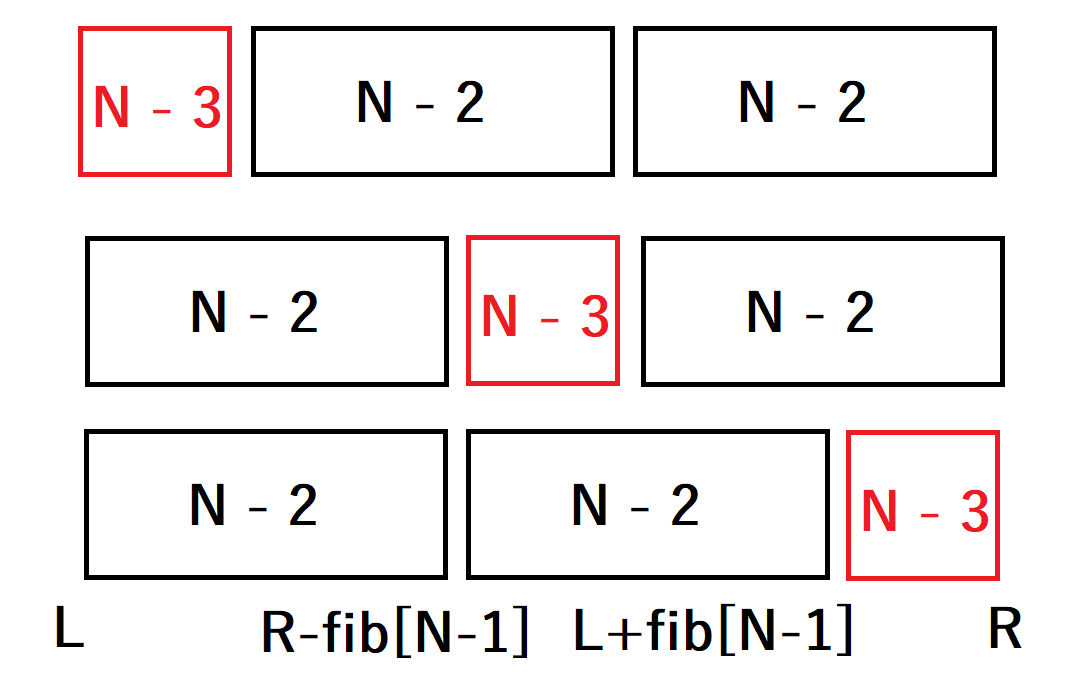
\(s_{N - 3}\)の区間を付随させる\(s_{N-2}\)が一意に定まる場合は良いですが、\(F_{5, 3} =\)
abaabの\(S_{N} = S_{N-2} + S_{N-3} + S_{N-2}\)のようにどちらの\(S_{N-2}\)にも付随させることができる場合があります。それだけでなく、\(S_{N} = S_{N-3} + S_{N-2} + S_{N-2}\)と\(S_{N} = S_{N-3} + S_{N-2} + S_{N-2}\)を両方満たしている\(F_{5,1}=\)ababaなどといったものもあります。このように\(N-1\)の区間として複数の候補が出てくる場合があります。
このような場合は、\(N\)の区間における \(k\) の値がなるべく小さくなる方向に選ぶと良いです。
まず、\(k\)の値が大きいとどのような不都合があるかについて説明します。具体例として、\(F_{5,1}=\)ababaを挙げます。これは、
ababa\(=\)aba\(+\)baababa\(=\)ab\(+\)aba
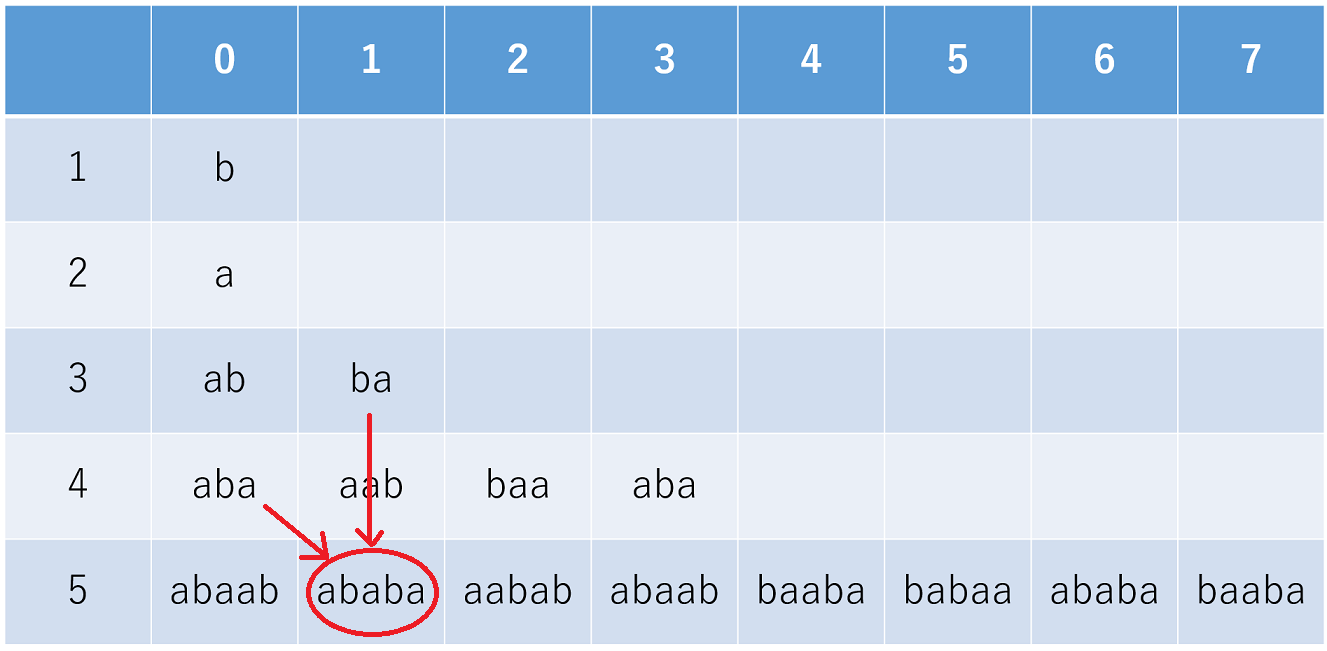
したがって、\(N-2\) の \(k\) の値は\(N-1\)、\(N\)よりも小さくなくてはいけないことを考えると、\(k\) の値はなるべく小さい方が良いことが分かります。また、\(F_{p,q}=s\)が存在することからそのように\(k\)を選ぶことで、漸化式が存在する範囲で遷移することが可能となります。
では、\(k\)を小さくするためにはどのように\(N-1\)の区間を選択すればよいでしょうか。そこで思い出して欲しいのが、
- 偶数のとき:\(s_{N} = s_{N - 1} + s_{N - 2}\) \(k_{N} = 2 k_{N-1}\)
- 奇数のとき:\(s_{N} = s_{N - 2} + s_{N - 1}\) \(k_{N} = 2 k_{N-1} + 1\)
しかし、先ほどみたababa\(=\)aba+baのように\(N\)の区間で前の区間を採用しているにも関わらず、\(k\)が最小となっていない場合がありました。これは、\(N-2\)の区間で反転が起こっていると、\(N-1\)では\(k\)の値は2倍、\(N\)では4倍となっているためです。このことから、\(N\)と\(N-1\)どちらかしか前の区間を採用できないという状況が発生した場合は、\(N\)では後ろの区間を採用し、\(N-1\)で前の区間を採用した方が良いことが言えます。すなわち、\(N-1\)の区間での\(k\)の最小化することが\(N\)の\(k\)の値を最小化することにつながります。
もう少し分かりやすい表現をすると、\(N=3\) の区間で反転状態が起きているか否かが最上位ビットが1であるか否か、\(N=4\) の区間で反転状態が起きているか否かが上から2番目のビットが1であるか否か、\(N=5\) の区間で反転状態が起きているか否かが上から3番目のビットが1であるか否か、\(\cdots\)、\(N=i\) の区間で反転状態が起きているか否かが上から\(i-2\)番目のビットが1であるか否かといったように続きます。
具体例として、入出力例1を見てみると、
入力例1
babba
出力例1
5
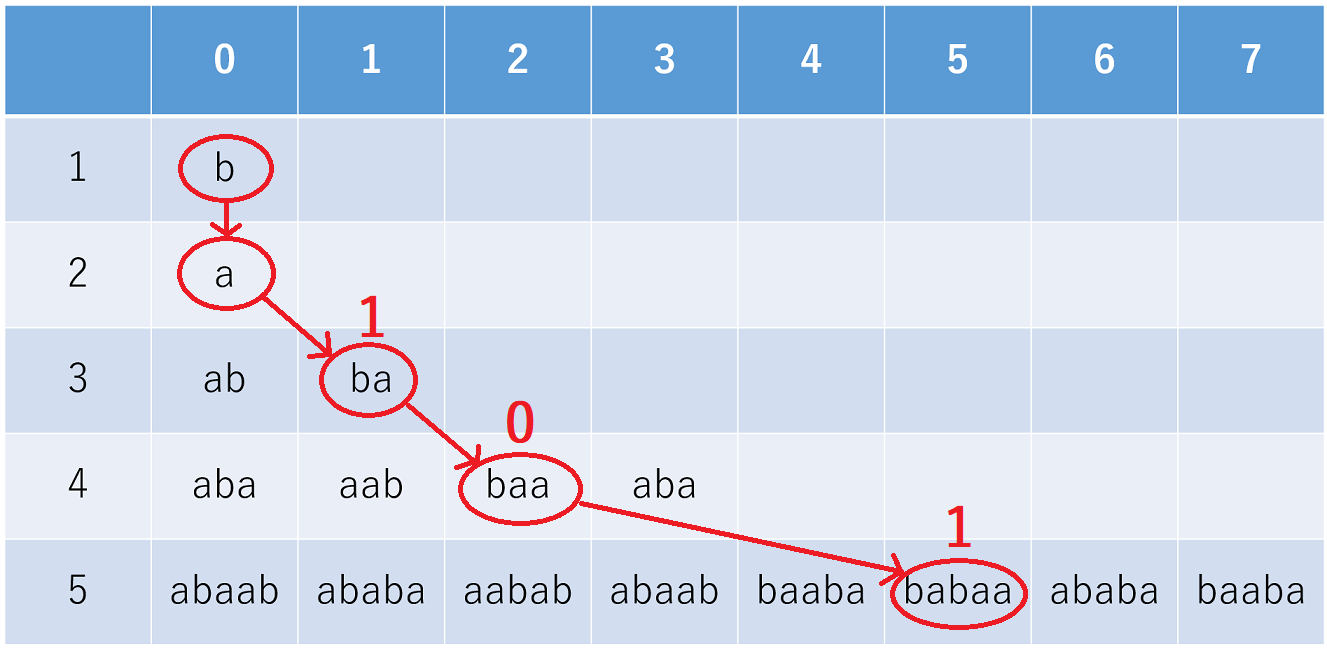
- \(N=3\)のとき:
ba\(=\)b\(+\)aなので反転が起きている - \(N=4\)のとき:
baa\(=\)ba\(+\)aなので反転が起きていない - \(N=5\)のとき:
baaba\(=\)ba\(+\)baaなので反転が起きている
101となり、これは確かに\(5\)となることが分かるかと思います。このように\(N\)が小さいところで\(k\)の値を最小化させた方が最終的な\(k\) を最小化できることが言えます。
\(N\)の区間においては\(N-2\)以下の区間における\(k\)を最小化することを直接考えることはできませんが、\(N-1\)の区間における\(k\)を考慮することができ、これを繰り返すことがより小さい\(N\)における\(k\)を最小化することに繋がります。
\(N\)の区間において\(N-1\)の区間における\(k\)の値を最小化する方法は、\(s_{N-1}=s_{N-2}+s_{N-3}\)となる区間を\(N-1\)の区間として選ぶことで、\(N-1\)の区間が反転していない状態となり、\(N-2\)の区間を前の区間として選ぶことができ、\(k\)の値がインクリメントされないことになります。よって、\(N\)の区間において\(s_{N-3}\)となっている部分は、後ろから\(s_{N-2}\)に付随させることが良いと言えます。
以下の画像は、\(s_{N}=s_{N-2}+s_{N-3}+s_{N-2}\)の型になっている\(N\)の区間において\(s_{N-3}\)を後ろから付随させた前区間\(s_{N-2}+s_{N-3}\)を選んだ時の\(N-1\)の状態と\(s_{N-3}\)を前から付随させた後区間\(s_{N-3}+s_{N-2}\)を選んだ時の\(N-1\)の状態を比較したものです。
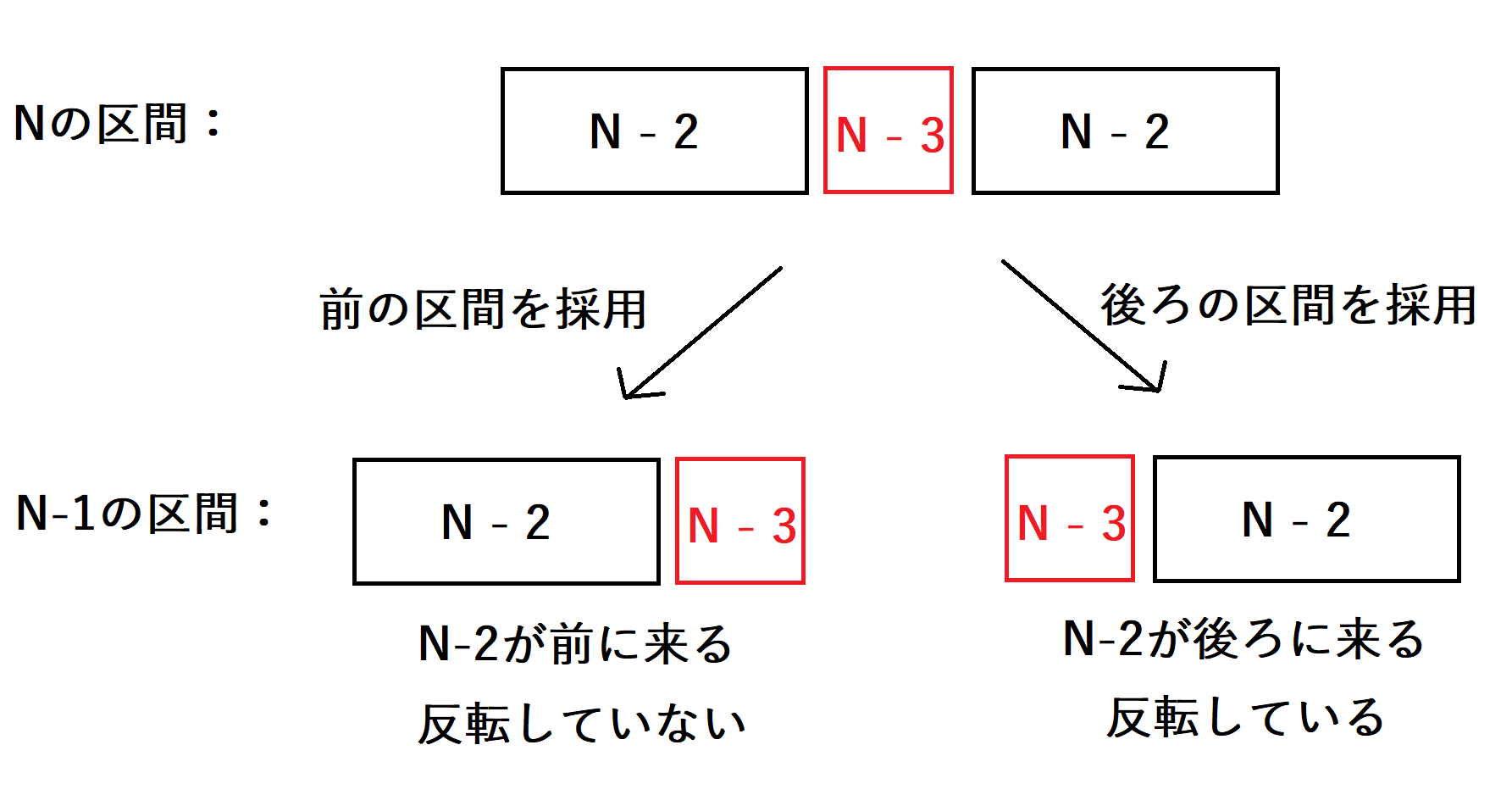
以上のことを踏まえて、\(N\)の区間の3つの型それぞれについてどのように\(N-1\)の区間を選ぶことが最適かを考えます。
- \(s_{N} = s_{N - 3} + s_{N - 2} + s_{N - 2}\)
- \(s_{N} = s_{N - 2} + s_{N - 3} + s_{N - 2}\)
- \(s_{N} = s_{N - 2} + s_{N - 2} + s_{N - 3}\)

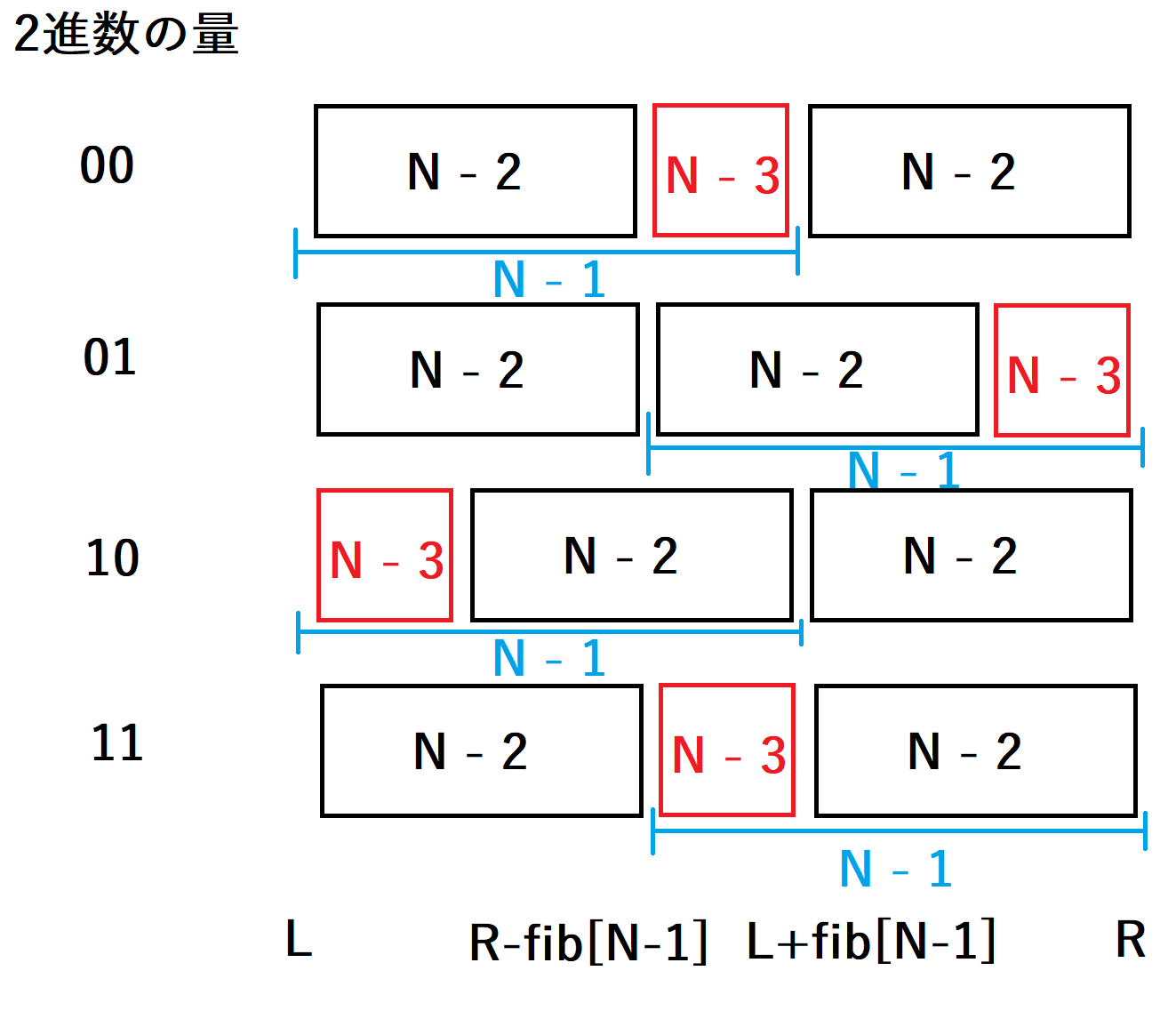
\(s_{N} = s_{N - 3} + s_{N - 2} + s_{N - 2}\)型については、候補はそもそも1つしかなく\(s_{N - 3}+s_{N-2}\)の前区間を\(N-1\)の区間として選ぶしか方法がありません。前区間を選んでいて、\(s_{N-3}\)が前から付随していることになるので、2進数で言うと
10の量に相当します。\(s_{N} = s_{N - 2} + s_{N - 3} + s_{N - 2}\)型については、\(s_{N - 2}+s_{N-3}\)の前区間と\(s_{N - 3}+s_{N-2}\)の後区間を選ぶ2通りがあります。\(N-1\)の区間として前区間を選んだ場合は、\(s_{N-3}\)は後ろから付随していることになるので、2進数で言うと
00の量に相当します。\(N-1\)の区間として後区間を選んだ場合は、\(s_{N-3}\)は前から付随していることになるので、2進数で言うと11の量に相当します。この場合は前区間を選んだ方が小さい値で済むことになりますので、前区間を選びます。\(s_{N} = s_{N - 2} + s_{N - 2} + s_{N - 3}\)型については、候補はそもそも1つしかなく\(s_{N - 2}+s_{N-3}\)の後区間を\(N-1\)の区間として選ぶしか方法がありません。後区間を選んでいて、\(s_{N-3}\)が後ろから付随していることになるので、2進数で言うと
01の量に相当します。
以上の選び方を2進数のオーダーが小さい順にならべると、
- \(s_{N} = s_{N - 2} + s_{N - 3} + s_{N - 2}\)型で前区間\([L,L+{\rm fib}[N-1])\)を\(N-1\)の区間として選ぶ \(k_{N}=2k_{N-1}\)
- \(s_{N} = s_{N - 2} + s_{N - 2} + s_{N - 3}\)型で後区間\([R-{\rm fib}[N-1],R)\)を\(N-1\)の区間として選ぶ \(k_{N}=2k_{N-1}+1\)
- \(s_{N} = s_{N - 3} + s_{N - 2} + s_{N - 2}\)型で前区間\([L,L+{\rm fib}[N-1])\)を\(N-1\)の区間として選ぶ \(k_{N}=2k_{N-1}\)
- \(s_{N} = s_{N - 2} + s_{N - 3} + s_{N - 2}\)型で後区間\([R-{\rm fib}[N-1],R)\)を\(N-1\)の区間として選ぶ \(k_{N}=2k_{N-1}+1\)
- \(s_{3}=\)
abのとき \(k_{3} = 0\) - \(s_{3}=\)
baのとき \(k_{3} = 1\)
実装例(C++)
#include<bits/stdc++.h>
using namespace std;
int main(){
string s;
cin >> s;
vector<int> fib(22);
fib[1] = 1;
for(int i = 2; i <= 21; i++)fib[i] = fib[i - 1] + fib[i - 2];
int start = lower_bound(fib.begin(), fib.end(), s.size()) - fib.begin();
if(s == "a")start++;
function<int(int,int,int)> rec = [&](int N, int l, int r){
if(N <= 3)return (N == 3 && s[l] == 'b'? 1 : 0);
string s1 = s.substr(l, fib[N - 2]);
string s2 = s.substr(r - fib[N - 2], fib[N - 2]);
if(s1 == s2)return 2 * rec(N - 1, l, l + fib[N - 1]);
s2 = s.substr(l + fib[N - 2], fib[N - 2]);
if(s1 == s2)return 2 * rec(N - 1, r - fib[N - 1], r) + 1;
return 2 * rec(N - 1, l, l + fib[N - 1]);
};
cout << start << " " << rec(start, 0, s.size()) << '\n';
}
コラム
本解法ではそこまで役に立つ性質ではないですが、他の解法だと役に立つかもしれない性質を2点ほど紹介します。1点目は、文字列\(F_{n,k}\)に含まれるaの文字数、bの文字数も\(n \geq 2\)においてはフィボナッチ数列になっている点です。\(F_{n,k}\)の文字数をフィボナッチ数列の第\(n\)項として、\({\rm fib}[n]\)と表すことにすると、aの文字数は\({\rm fib}[n-1]\)、bの文字数は\({\rm fib}[n-2]\)となっており、全体で
\[ {\rm fib}[n] = {\rm fib}[n-1] + {\rm fib}[n-2] \]
が成り立っていることも分かるかと思います。ちなみに、\(n\)における文字列の種類数も\({\rm fib}[n]\)となっており、 \(n\)における文字数と登場する文字列の種類数は等しくなっています。
2点目は、\(n \geq 3\)において、同一 \(n\) 上の文字列\(F_{n,k}\)について \(0 \leq k < 2^{n-2}\) の列挙を行うと、文字の位置が鏡対称的に現れている点です。\(k = 2^{n-3} - 1\)と\(k = 2^{n-3}\)の間を境界として、\(k_{1} {\rm xor} k _ {2} (= k_{1} + k_{2}) = 2^{n-2} - 1\)を満たす文字列\( F_{n,k_{1}} \) と \( F_{n,k_{2}} \) は互いに文字列の順番を反転させた関係にあります。
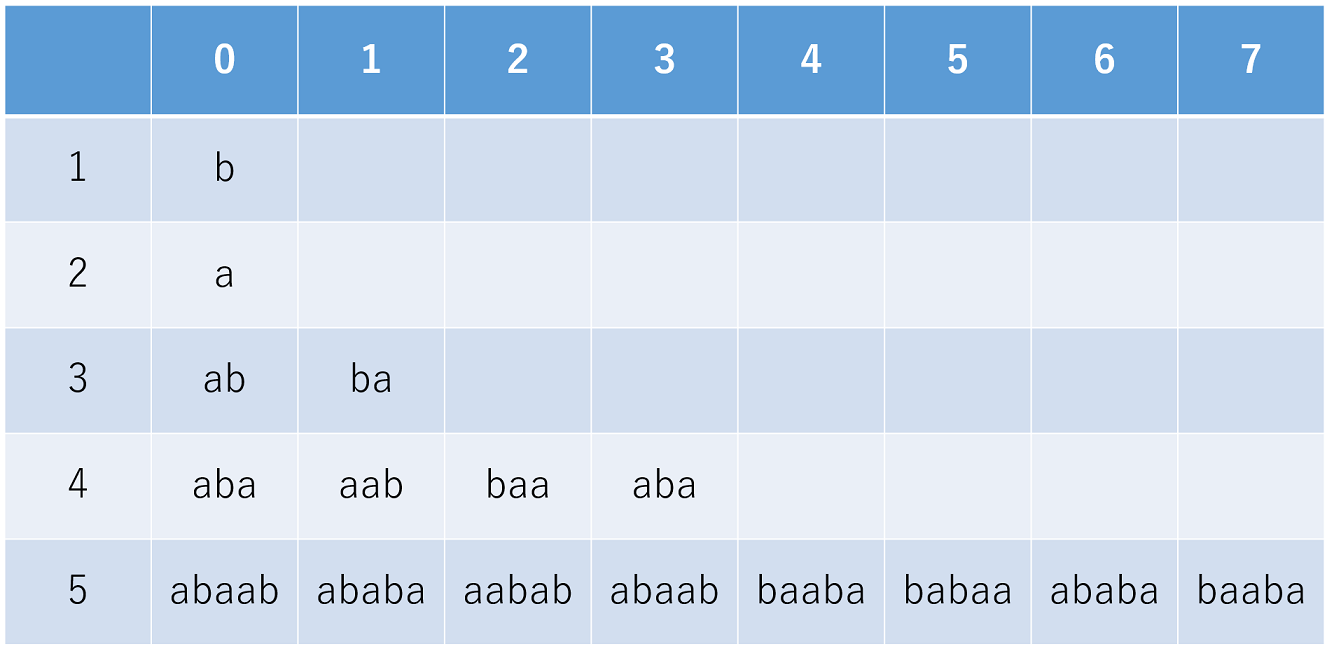
実際に見てみると、
\(n=3\) について
- \(0 \,{\rm xor}\,1 = 1\):\(F_{3,0}\)=
abと\(F_{3,1}\)=ba
- \(0 \,{\rm xor}\,3 = 3\):\(F_{4,0}\)=
abaと\(F_{4,3}\)=aba - \(1 \,{\rm xor}\,2 = 3\):\(F_{4,1}\)=
aabと\(F_{4,2}\)=baa
- \(0 \,{\rm xor}\,7 = 7\):\(F_{5,0}\)=
abaabと\(F_{5,7}\)=baaba - \(1 \,{\rm xor}\,6 = 7\):\(F_{5,1}\)=
ababaと\(F_{5,6}\)=ababa - \(2 \,{\rm xor}\,5 = 7\):\(F_{5,2}\)=
aababと\(F_{5,5}\)=babaa - \(3 \,{\rm xor}\,4 = 7\):\(F_{5,3}\)=
abaabと\(F_{5,4}\)=baaba
この性質を利用すると、文字列\(s\)先頭文字が
bであった場合は、文字列\(s\)を反転させたものの答え\(ans\)を求めて最後に\(ans \,{\rm xor}\,(2^{n-2} - 1)\)を行うことで\(k\)の値を求めることも可能です。本解法で言うと、\(n=3\)の場合分けを最初に行うことに相当します。すなわち、\(n \geq 3\)において\(k \geq 2 ^ { n-3}\)となる\(k\) の後半部分を見ないことに相当します。後半部分にも
aが先頭文字となる\(F_{5,6}=\)ababaや\(F_{6,15}=\)ababaabaのようなものもありますが、このような文字については\(F_{5,6}=F_{5,1}=\)ababa、\(F_{6,15}=F_{6,2}=\)ababaabaといったように前半部分でより小さい\(k\)が存在します。実は、先頭文字が
bとなる文字列、\(k \geq 2 ^ { n-3}\)において先頭文字がaとなる文字列の個数はそれぞれJacobsthal numberと呼ばれるものの数に従って増えています。Jacobsthal numberは第\(n\)項を\(J[n]\)とすると、以下の漸化式に従っています。
\[ J[n]=\left\{ \begin{array}{cc} 0& {\rm if}\,\,n =0\\ 1& {\rm if}\,\,n =1\\ J[n-1]+2J[n-2]& {\rm otherwise}\\ \end{array}\right. \]
始めの数項を書き出してみると\(0,1,1,3,5,11,21,43,85,171\)のようになっています。本問題では、\(n\geq 3\)において先頭文字がbとなる文字列の個数は\(J[n-2]\)、\(k \geq 2 ^ { n-3}\)において先頭文字がaとなる文字列の個数は\(J[n-3]\)と表すことができます。また、先頭文字がbとなる文字列の個数がすべて\(k \geq 2 ^ { n-3}\)となっていることを考えると、\(J[n-2]+J[n-3]=2^{n-3}\)になることが分かるかと思います。Jacobsthal numberの隣接項の和が2のべき乗となっていることが確認できます。
bが先頭文字となっているものをあらかじめ反転しておく実装を取り入れたものが以下のものになります。
実装例(C++)
#include<bits/stdc++.h>
using namespace std;
int main(){
string s;
cin >> s;
vector<int> fib(22);
fib[1] = 1;
for(int i = 2; i <= 21; i++)fib[i] = fib[i - 1] + fib[i - 2];
int start = lower_bound(fib.begin(), fib.end(), s.size()) - fib.begin();
if(s == "a")start++;
bool rev_flag = false;
if(start >= 3 && s[0] == 'b'){
reverse(s.begin(), s.end());
rev_flag = true;
}
function<int(int,int,int)> rec = [&](int N, int l, int r){
if(N <= 3)return 0;
string s1 = s.substr(l, fib[N - 2]);
string s2 = s.substr(r - fib[N - 2], fib[N - 2]);
if(s1 == s2)return 2 * rec(N - 1, l, l + fib[N - 1]);
s2 = s.substr(l + fib[N - 2], fib[N - 2]);
if(s1 == s2)return 2 * rec(N - 1, r - fib[N - 1], r) + 1;
return 2 * rec(N - 1, l, l + fib[N - 1]);
};
cout << start << " " << (rec(start, 0, s.size()) ^ (rev_flag ? (1 << start - 2) - 1 : 0)) << '\n';
}
posted:
last update:
