E - Enormous XOR Rectangle Editorial /

Time Limit: 2 sec / Memory Limit: 256 MB

Problem

Cat Snuke received a paper that has been divided into grids having H horizontal rows and W vertical columns as a birthday gift. For each block a number is written as shown in the figure below.

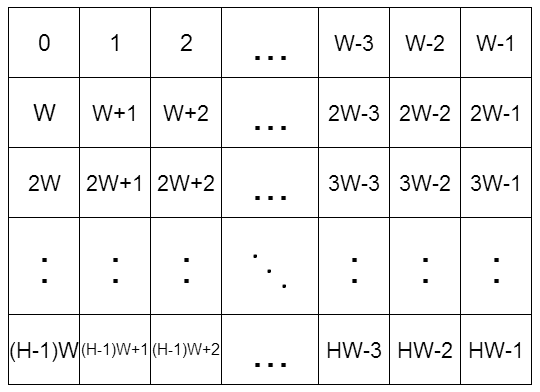
sample

More precisely, the number, which is written in the i_{th} row from the top of the rectangle paper and j_{th} column from the left of the rectangle paper, is (i - 1) \times W + (j - 1).

Cat Snuke wants to choose a partial rectangle from this rectangle paper, then find the value obtained by bitwise xor for all the numbers in this partial rectangle. Specifically, Cat Snuke will choose integers t,b(1≦t≦b≦H),l,r(1≦l≦r≦W), then calculate the value obtained by bitwise xor for all the numbers in the area from the top of the rectangle between the t_{th} row and the b_{th} row (including both ends), form the left of the rectangle between the l_{th} column and r_{th} column (including both ends).

Cat Snuke is able to choose any values for t,b,l,r. Please calculate the maximum value that can be obtained.

Input

Inputs will be given by standard input in following format

H W
  • At the first line, H(1≦H≦1,000,000,000), W(1≦W≦1,000,000,000) , will be given divided by space.

Output

Please calculate the maximum value that can be obtained, then output it in one line.

Print a newline at the end of output.

Input Example 1

4 5

Output Example 1

31
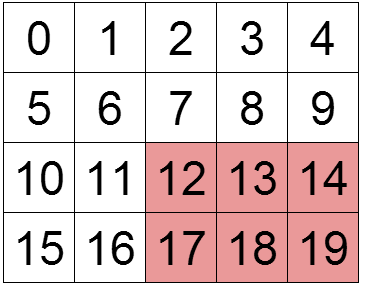
sample

For example, the obtained value of t=3,b=4,l=3,r=5 is 12 xor 13 xor 14 xor 17 xor 18 xor 19 = 31, this is the maximum value that can be obtained in this case.

Input Example 2

314159265 358979323

Output Example 2

144115188075855871