 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
Cat Snuke and Wolf Sothe are going to play a kind of game to celebrate the new year. There are N designed levels of blocks, on the top of the blocks there is a Daruma doll (a kind of Japanese traditional ornament). 2 players will keep removing blocks one by one alternately and keep the Daruma on the top.
The following figure shows an example of blocks, the placement of the odd-numbered level (from the bottom) blocks, and the placement of the even-numbered level (from the bottom) blocks.
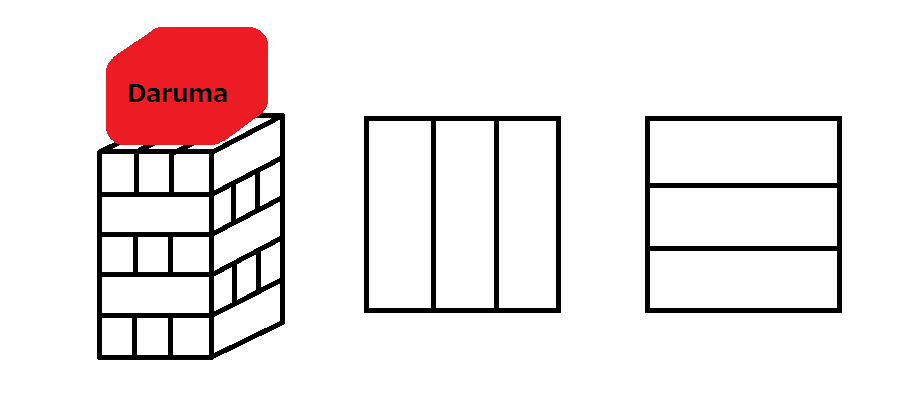
Here is an example of blocks (the figure on the left), the plan view of the placement of the odd-numbered level (from the bottom) blocks (the figure in the middle), and the plan view of the placement of the even-numbered level (from the bottom) blocks (the figure on the right).
Cat Snuke starts first, then they repeat removing one block each time from the remaining blocks in turn (alternately). However, it is not allowed for a player to remove a block if removing this block will cause unstable placement of the rest blocks. Any other blocks are allowed to be removed. If there are only blocks that are not allowed to be removed, the player who is in turn loses the game.
Unstable Placement is defined as follows: among the N level blocks there are 1 or more levels that have no block or only have 1 block on the end of either side on that level.
The status of an ongoing game will be given. Because Cat Snuke starts first, if there are even number blocks that have been removed, then the next turn is Cat Snuke’s. Otherwise, if there are odd number blocks that have been removed, the next turn is Wolf Sothe’s. Please decide which player will finally win if both of them play as best as they can.
Input
Inputs will be given by standard input in following format.
N
c_{1, 1, 1}c_{1, 1, 2}c_{1, 1, 3}
c_{1, 2, 1}c_{1, 2, 2}c_{1, 2, 3}
c_{1, 3, 1}c_{1, 3, 2}c_{1, 3, 3}
c_{2, 1, 1}c_{2, 1, 2}c_{2, 1, 3}
c_{2, 2, 1}c_{2, 2, 2}c_{2, 2, 3}
c_{2, 3, 1}c_{2, 3, 2}c_{2, 3, 3}
:
c_{N, 1, 1}c_{N, 1, 2}c_{N, 1, 3}
c_{N, 2, 1}c_{N, 2, 2}c_{N, 2, 3}
c_{N, 3, 1}c_{N, 3, 2}c_{N, 3, 3}
- At the first line, an integer N(1≦N≦50,000) will be given.
- From the second line there are 3N additional lines to give the status of an ongoing game. In these lines, from the 3i -2_{th} line to the 3i_{th} line there is information about the i_{th} level (from the bottom) blocks. At the 3(i-1) + j(1≦i≦N,1≦j≦3) line, c_{i, j, 1}, c_{i, j, 2}, c_{i, j, 3} will be given without any separator. These are either
#or.. If c_{i, j, k} is#, it means that the block that in the corresponding position (please refer to the figure below) of i_{th} level (from the bottom) has NOT been removed. If c_{i, j, k} is., it means that the block that in the corresponding position of i_{th} level (from the bottom) has been removed. - If i(1≦i≦N) is odd, for k = 1, 2, 3, c_{i, 1, k} = c_{i, 2, k} = c_{i, 3, k}.
- If i(1≦i≦N) is even, for j = 1, 2, 3, c_{i, j, 1} = c_{i, j, 2} = c_{i, j, 3}
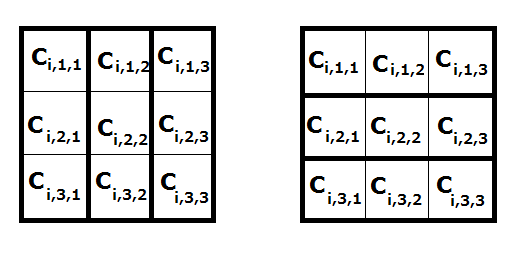
The figure on the left shows the plan view of the corresponding placement of the odd-numbered level (from the bottom) blocks. The figure on the right shows the plan view of the corresponding placement of the even-numbered level (from the bottom) blocks.
There is no input that has already been an unstable placement .
Output
Please decide which player will finally win if both of them play as best as they can. If Cat Snuke wins, output Snuke in one line. Otherwise, if Wolf Sothe wins, output Sothe in one line.
Print a newline at the end of output.
Input Example 1
2 #.# #.# #.# ### ### ...
Output Example 1
Snuke
If cat Snuke removes the block on the end of side that has not been removed on the 2nd level (from the bottom), Wolf Sothe will have no block that can be removed.
Input Example 2
4 ### ### ### ... ### ### ##. ##. ##. ### ### ###
Output Example 2
Sothe
Input Example 3
4 ### ### ### ... ### ### .#. .#. .#. ### ### ###
Output Example 3
Sothe
Please note that there are 3 blocks that have been removed by the input status, thus the next turn is Wolf Sothe’s.