 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
Problem
There is a 2-dimensional grid of size R \times C. There are many explosives warehouses on some of the cells.
When a warehouse catches fire, it finally explodes at some time in the future. When a warehouse explodes, it blasts in a + shape with fire extending on all four side. Blast fire extends until it reaches other warehouse. Blast fire won't reach the cells behind those warehouses.
A warehouse exposed to blast fire may catch fire or may not catch fire. A warehouse that once exposed to blast fire but didn't catch fire then, can be exposed to another blast fire. In that case, it's same as before, the warehouse may catch fire or may not catch fire.
An exploded warehouse won't catch fire anymore but still blocks the blast fire.
At first, you lit fire on one explosives warehouse. Finally, all warehouses had exploded.
During that disaster, no warehouses exploded at the same time. (Some of the warehouses could have caught fire at the same time.)
Calculate the number of possible ways of exploding that all warehouses explodes. As the answer can be rather large, print it as a remainder after dividing it by number 1000000009(10^9+9).
Ways of exploding is a set of pairs of warehouses. Each pair is a warehouse which caught fire and the warehouse which put fire on the former warehouse by exploding. When two ways of exploding have at least one different pair of warehouses, they are distinct.
Input
Input is given in the following format.
R C
s_{(1,1)}s_{(1,2)} .. s_{(1,C)}
s_{(2,1)}s_{(2,2)} .. s_{(2,C)}
:
s_{(R,1)}s_{(R,2)} .. s_{(R,C)}
a b
- On the first line you will be given two integers R,C (1 \leq R,C \leq 16) separated by space, the number of rows and columns of the grid, respectively.
- Following R lines is the place of warehouses.
Each line contains a string of size C. Each string consists of
.andW. The i-th (1 \leq i \leq R) line's j-th (1 \leq j \leq C) character represents the cell (i,j). If the character is., the cell (i,j) is an empty cell. If the character isW, a warehouse is on the cell (i,j). - On the next line, you will be given two integers a,b (1 \leq a \leq R,1 \leq b \leq C) separated by space. (a,b) is the place of the warehouse you first put fire on. It is guaranteed that there is a warehouse on this cell.
- It is guaranteed that there is at least 1 warehouse.
Output
Output one line containing the number of ways of exploding all warehouses modulo 1000000009. Make sure to insert a line break at the end of the output.
Input Example 1
3 4 W.W. .... W.W. 1 1
Output Example 1
4
For example, there is one way of exploding like below. Including this way, there are 4 ways of exploding.
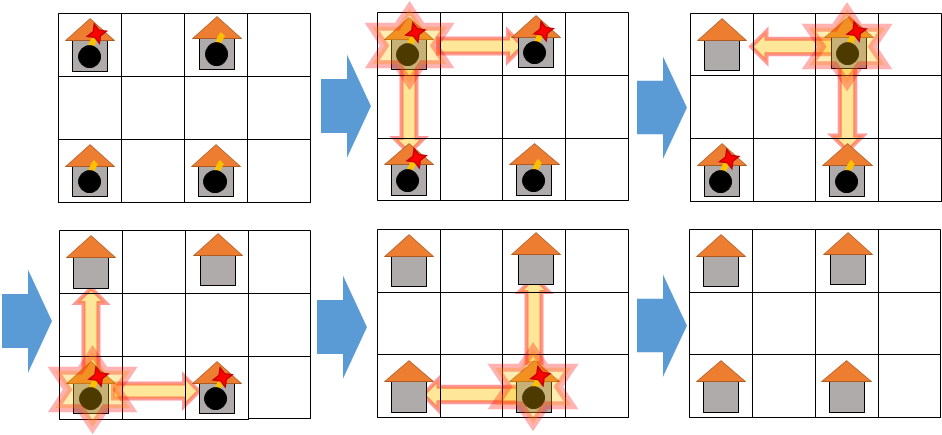
In this way, the warehouses at (1,3) and (3,1) caught fire from warehouse at (1,1), and the warehouse at (3,3) caught fire from warehouse of (3,1)
Input Example 2
3 4 W.W. .W.W W.W. 2 2
Output Example 2
0
Not all warehouses can explode in this case.
Input Example 3
1 1 W 1 1
Output Example 3
1
Input Example 4
16 16 WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW WWWWWWWWWWWWWWWW 1 1
Ouput Example 4
242986351
Don't forget to output the remainder after dividing the number by 1,000,000,009.