 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MiB
配点 : 1500 点
問題文
N 頂点の連結な無向グラフがあり、頂点には 1~N の番号が付いています。 辺の長さはすべて 1 です。 各 i (1≦i≦N) について、頂点 1 と頂点 i の距離が A_i、頂点 2 と頂点 i の距離が B_i であることが分かっています。 このようなグラフが存在するかを判定してください。また、存在する場合は、辺の本数として考えられる最小値を求めてください。
制約
- 2≦N≦10^5
- 0≦A_i,B_i≦N-1
入力
入力は以下の形式で標準入力から与えられる。
N A_1 B_1 A_2 B_2 : A_N B_N
出力
条件を満たすグラフが存在する場合は辺の本数の最小値を、存在しない場合は -1 を出力せよ。
入力例 1
4 0 1 1 0 1 1 2 1
出力例 1
4
下図のような 2 種類のグラフが考えられますが、右のグラフの方が辺の本数が少ないです。
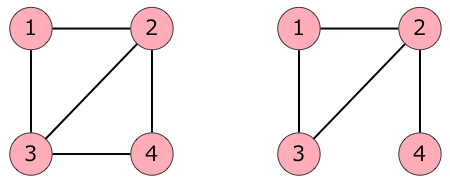
入力例 2
3 0 1 1 0 2 2
出力例 2
-1
このようなグラフは存在しません。
Score : 1500 points
Problem Statement
There is an undirected connected graph with N vertices numbered 1 through N. The lengths of all edges in this graph are 1. It is known that for each i (1≦i≦N), the distance between vertex 1 and vertex i is A_i, and the distance between vertex 2 and vertex i is B_i. Determine whether there exists such a graph. If it exists, find the minimum possible number of edges in it.
Constraints
- 2≦N≦10^5
- 0≦A_i,B_i≦N-1
Input
The input is given from Standard Input in the following format:
N A_1 B_1 A_2 B_2 : A_N B_N
Output
If there exists a graph satisfying the conditions, print the minimum possible number of edges in such a graph. Otherwise, print -1.
Sample Input 1
4 0 1 1 0 1 1 2 1
Sample Output 1
4
The figure below shows two possible graphs. The graph on the right has fewer edges.

Sample Input 2
3 0 1 1 0 2 2
Sample Output 2
-1
Such a graph does not exist.