 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 900 点
問題文
H \times W のマス目があります。上から i 行目、左から j 列目のマスを (i,j) で表します。
各マスは空きマス・壁マスのいずれかであり、その情報は H \times W 個の文字 S_{1,1},\dots ,S_{H,W} によって表されます。
マス (i,j) は、S_{i,j} が . のとき空きマス、# のとき壁マスです。
はじめ、高橋君がマス (1,1) にいます。 高橋君は、今いるマスと上下左右のいずれかの方向に隣接するマスに移動することを好きな回数行うことが出来ます。 ただし、2 回続けて同じ方向に移動することは出来ません。 また、壁マスやマス目の外に移動することも出来ません。
高橋君は移動を開始する前に 0 個以上の壁マスを破壊して空きマスに変化させることが出来ます。 高橋君がマス (H,W) に辿り着くためには、最小でいくつの壁マスを破壊する必要があるでしょうか? この問題の制約下において、マス (H,W) に辿り着くことが出来るように壁マスを破壊する方法が存在することは証明出来ます。
T 個のテストケースが与えられるので、それぞれについて答えを求めて下さい。
制約
- 1 \le T \le 1000
- 2 \le H, W \le 100
- S_{i,j} は
.または# - S_{1,1} および S_{H,W} は
. - 全てのテストケースにおける HW の総和は 3 \times 10^4 以下
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケースは以下の形式で与えられる。
H W
S_{1,1}S_{1,2}\ldotsS_{1,W}
S_{2,1}S_{2,2}\ldotsS_{2,W}
\vdots
S_{H,1}S_{H,2}\ldotsS_{H,W}
出力
T 行出力せよ。
i 行目には i 番目のテストケースについて、高橋君がマス (H,W) に辿り着くために破壊する壁マスの個数としてありうる最小値を出力せよ。
入力例 1
3 3 5 ..##. .#... ##.#. 2 3 ..# #.. 13 13 .############ ##.##..###..# #.#.#.#.#.### #...#..##.### #.#.#.#.#.### #.#.#.#.##..# ############# #...##.##.#.# ###.#..##.#.# #...##.##...# #.####.####.# #...#...###.# ############.
出力例 1
2 0 13
1 つ目のテストケースについて、下図のように 2 個の壁マスを破壊することでマス (H,W) に辿り着く事が出来ます。
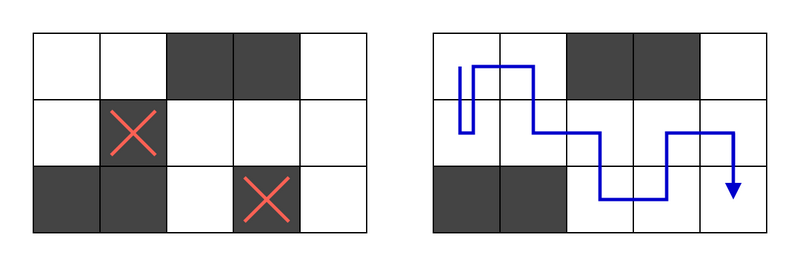
左側は破壊する壁マスの例を表しており、右側は移動経路の例を表しています。 必ずしも移動回数を最小化する必要がない点や、同じマスに 2 回以上訪れても良い点に注意して下さい。
2 つ目のテストケースについて、壁マスを 1 つも破壊せずにマス (H,W) に辿り着くことが出来ます。
Score : 900 points
Problem Statement
There is an H \times W grid. Let (i,j) denote the cell at the i-th row from the top and j-th column from the left.
Each cell is an empty cell or a wall cell, and this information is represented by H \times W characters S_{1,1},\dots ,S_{H,W}.
Cell (i,j) is an empty cell if S_{i,j} is ., and a wall cell if it is #.
Initially, Takahashi is at cell (1,1). He can move to a cell adjacent to his current cell in one of the four directions (up, down, left, right) any number of times. However, he cannot move in the same direction twice in a row. Also, he cannot move to a wall cell or outside the grid.
Before starting to move, he can destroy zero or more wall cells to change them into empty cells. What is the minimum number of wall cells he needs to destroy to reach cell (H,W)? Under the constraints of this problem, it can be proved that there exists a way to destroy wall cells so that he can reach cell (H,W).
You are given T test cases; solve each of them.
Constraints
- 1 \le T \le 1000
- 2 \le H, W \le 100
- S_{i,j} is
.or#. - S_{1,1} and S_{H,W} are
.. - The sum of HW over all test cases is at most 3 \times 10^4.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case is given in the following format:
H W
S_{1,1}S_{1,2}\ldotsS_{1,W}
S_{2,1}S_{2,2}\ldotsS_{2,W}
\vdots
S_{H,1}S_{H,2}\ldotsS_{H,W}
Output
Output T lines.
The i-th line should contain the minimum possible number of wall cells to destroy for Takahashi to reach cell (H,W) for the i-th test case.
Sample Input 1
3 3 5 ..##. .#... ##.#. 2 3 ..# #.. 13 13 .############ ##.##..###..# #.#.#.#.#.### #...#..##.### #.#.#.#.#.### #.#.#.#.##..# ############# #...##.##.#.# ###.#..##.#.# #...##.##...# #.####.####.# #...#...###.# ############.
Sample Output 1
2 0 13
For the first test case, Takahashi can reach cell (H,W) by destroying two wall cells as shown below.

The left side shows an example of wall cells to destroy, and the right side shows an example of a movement path. Note that it is not necessary to minimize the number of moves, and it is allowed to visit the same cell more than once.
For the second test case, he can reach cell (H,W) without destroying any wall cells.