Hints: https://atcoder.jp/contests/arc210/editorial/14585

For simplicity, we write A for Alice and B for Bob.

Also, following graph theory conventions, we write \(P_n\) for a path consisting of \(n\) vertices and \(C_n\) for a cycle consisting of \(n\) vertices.

---

[1] When \(N\) is odd

The following holds:

• [A1] If \(N\) is odd and \(G\) does not contain \(P_3\) as a subgraph, then A can win.
• [B1] If \(N\) is odd and \(G\) contains \(P_3\) as a subgraph, then B can win.

We show [A1]. In this case, the size of each connected component is \(1\) or \(2\). To show that A can win, it suffices to show that A can win even if we add edges as necessary. Therefore, it suffices to show the following:

• In a graph where the connected components are one isolated vertex and several \(P_2\)s, A can win.

Considering induction starting from one isolated vertex, we need to show the following:

• If A can win when playing the game on graph \(G\), then A can also win when playing the game on the graph obtained by adding one \(P_2\) to \(G\).

Let \(x,y\) be the added vertices. A should choose the other vertex immediately after B chooses either \(x\) or \(y\), and otherwise reproduce the winning strategy on \(G\). However, if B never chooses \(x\) or \(y\) and there are two vertices remaining on A’s turn, then \(x\) and \(y\) should be chosen by A and B in that order. This proves [A1].

We show [B1]. To show that B can win, it suffices to show that B can win even if we remove edges as necessary. Therefore, it suffices to show the following:

• In a graph where the connected components are one \(P_3\) and an even number of isolated vertices, B can win.

Considering induction starting from \(P_3\), we need to show the following:

• If B can win when playing the game on graph \(G\), then B can also win when playing the game on the graph obtained by adding two isolated vertices to \(G\).

This can be proved in exactly the same way as we proved [A1].

This completes the discussion for when \(N\) is odd.

---

[2] When \(N\) is even

• [B2] If \(N\) is even and \(G\) contains two \(P_3\)s that do not share vertices as subgraphs, then B can win.
• [B3] If \(N\) is even and \(G\) contains \(C_4\) as a subgraph, then B can win.
• [B4] If \(N\) is even and \(G\) contains the graph obtained by attaching a leaf to each vertex of \(C_3\) (the rightmost graph in the figure below), then B can win.

This can also be proved by induction similar to 1.

Below, under the assumption that [B2], [B3], [B4] do not hold, we prove that A can win. In particular, note that since [B2] does not hold, there is at most one connected component with three or more vertices.

We proceed by case analysis on the number of vertices with degree \(3\) or more.

[2-1] zero vertices with degree \(3\) or more

In this case, a connected component with \(3\) or more vertices is a path or a cycle. Under the condition that [B2], [B3] do not hold, this component is one of \(P_3, P_4, P_5, C_3, C_5\). Therefore, it suffices to show the following:

• [A2] If \(N\) is even and all connected components of \(G\) have at most two vertices, then A can win.
• [A3] If \(N\) is even and the connected component of \(G\) with three or more vertices is unique and is one of \(P_3, P_4, P_5, C_3, C_5\), then A can win.

Again, these can be proved by the same proof as when we showed [A1].

[2-2] one vertex with degree \(3\) or more

Let \(v\) be this vertex with degree \(3\) or more. Then, all connected components of \(G-v\) are isolated vertices or paths. From the assumption that [B2], [B3] do not hold, it suffices to show the following:

• [A4] If \(N\) is even and \(G\) has a unique vertex with degree \(3\) or more, and letting \(v\) be that vertex, all connected components of \(G-v\) have at most two vertices, then A can win.

We prove that A can win even with the additional rule “\(v\) must not be chosen.” By adding this rule, the edges connecting to \(v\) can be ignored. After adding edges appropriately, it suffices to show the following:

• In a graph consisting of a special vertex \(v\), one isolated vertex, and several \(P_2\)s, with the additional rule “A must not choose \(v\),” A can win.

In this case, again adding \(P_2\) preserves A’s victory, so it can be proved by induction.

[2-3] two or more vertices with degree \(3\) or more

Under the condition that [B2], [B3] do not hold, we can see that there are exactly two vertices with degree \(3\) or more, their degrees are exactly \(3\), they are adjacent, and they share exactly one neighbor. That is, \(G\) contains the following graph as a subgraph:

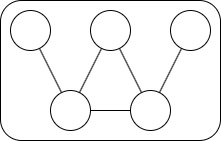
Furthermore, if [B4] also does not hold, it can be shown that there are no other edges or vertices in this connected component. Therefore, the only case we have not discussed yet is the following:

• [A5] If \(N\) is even and one of the connected components of \(G\) is the graph above, and all other connected components are only isolated vertices and \(P_2\)s, then A can win.

This can also be proved by induction similar to before.

---

[3] Summary

A’s winning conditions are [A1], [A2], [A3], [A4], [A5]. B’s winning conditions are [B1], [B2], [B3], [B4]. From the discussion so far, these exhaust all case divisions. By appropriately implementing the winning conditions of one player, we can solve this problem in \(O(N+M)\) time.

Note that for appropriately small graphs, implementation and consideration can be simplified by exhaustive search. For example, in the [2-3] case, when [B2] does not hold, it can be proved that the number of vertices in the connected component is at most some constant, so if you perform exhaustive search in such cases, there is no need to discover or implement [B4] or [A5].