F - ± ab 解説
by  maspy
maspy
ヒント集 → https://atcoder.jp/contests/arc210/editorial/14522
[1] コストのマンハッタン距離による言い換え
\(A_i=ax_i+by_i\) となる \((x_i,y_i)\) をひとつとり固定します.
操作は,\(x_i\) や \(y_i\) に対するインクリメント・デクリメントだと考えられます.これらにコスト \(s,t\) がかかるので,
- \(A_i\) を \(B_j\) にするためのコスト \(\mathrm{cost}(A_i\to B_j)\) は,\((sx_i,ty_i)\) から \((sz, tw)\) へのマンハッタン距離としてありうる最小値である.ただし,\((z,w)\) は \(B_j=az+bw\) となるような \((z,w)\) を動く.
さらに,適当なスワップにより,\(bs\geq at\) を仮定します.このとき,最適解であって \(x_i\) に対するインクリメント・デクリメントの回数は \(b\) 回未満であるものが存在します.これは \(b\) 回の \(+a\) 操作を \(a\) 回の \(+b\) 操作に取り換えるといったことを考えれば証明できます.
このことを踏まえて,\(x_i, y_i\) を \(0\leq x_i<b\) を満たすようにとっておきます.すると,目標となる \((z,w)\) は \(-b\leq z < 2b\) を満たすことになります.このような \((z,w)\) は \(B_j\) ごとに \(3\) つしかありません.
この状況を整理すると以下のようになります.
- \(2\) 次元平面上の点 \(P_i\) を次のように定める:\(A_i=ax+by\), \(0\leq x<b\) としたとき \(P_i(sx,ty)\).
- さらに \(Q_j, R_j, S_j\) を次のように定める:\(B_j=az+bw\), \(0\leq z<b\) としたとき \(Q_j(s(z-b),t(w+a))\), \(R_j(sz,tw)\), \(S_j(s(z+b),t(w-a))\).
- すると,\(\mathrm{cost}(A_i\to B_j)\) は,\(\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\) に等しい.ただし,\(\mathrm{dist}\) はマンハッタン距離である.
[2] 答の計算
- \(\mathrm{dist}(P_i,Q_j)=\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\)
- \(\mathrm{dist}(P_i,R_j)=\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\)
- \(\mathrm{dist}(P_i,S_j)=\min\{\mathrm{dist}(P_i,Q_j),\mathrm{dist}(P_i,R_j),\mathrm{dist}(P_i,S_j)\}\)
それぞれを満たす \(P_i\) 全体がどのような領域になるかを平面上に図示すると,次の図のようになります.
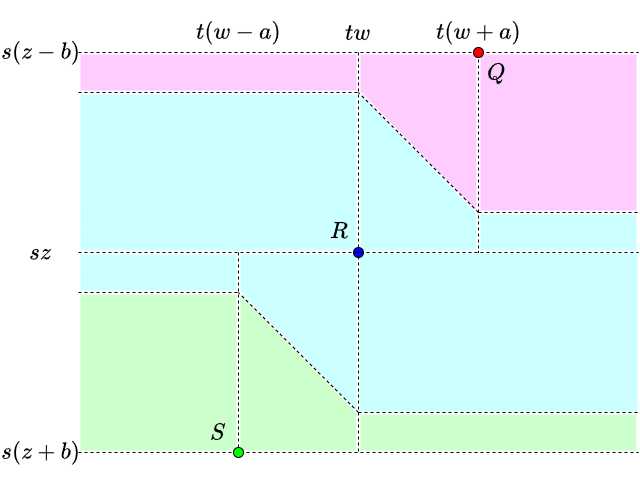
よって答を求めるには,点線で分割された \(12\) 領域のそれぞれについて,その領域内にある \(P_i\) の個数や,\(x\) 座標,\(y\) 座標の総和が求められればよいです.
あとは基本的な矩形クエリに関する問題です.台形領域については,次のようにある方向に無限に伸びる \(2\) つの領域の差として表すことで,(適当な座標変換のもとで)やはり矩形クエリに帰着できます.
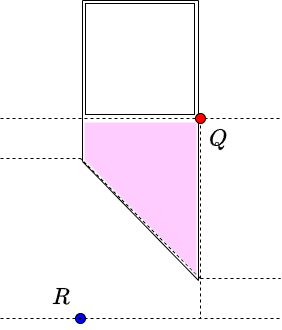
以上により,本問題は \(O((N+Q)(\log N+\log Q))\) 時間程度で解くことができます.複数の領域を正確に指定する必要があって少し大変ですが,\([s(z-b),sz)\) 部分と \([sz,s(z+b))\) 部分で行うべき処理は同じ形であることなどから,いくらか実装が簡略化できると思います.
投稿日時:
最終更新: