ヒント集 → https://atcoder.jp/contests/arc210/editorial/14522

簡単のため Alice を A，Bob を B と書きます．

また，グラフ理論の慣習にならって，\(n\) 頂点からなるパスを \(P_n\)，\(n\) 頂点からなるサイクルを \(C_n\) と書くことにします．

---

[1] \(N\) が奇数の場合

次が成り立ちます．

• [A1] \(N\) が奇数で \(G\) が \(P_3\) を部分グラフとして含まないならば，A が勝てる．
• [B1] \(N\) が奇数で \(G\) が \(P_3\) を部分グラフとして含むならば，B が勝てる．

[A1] を示します．この場合，各連結成分の大きさは \(1\) または \(2\) です．A が勝てることを示すためには，必要なら辺を増やした上で A が勝てることを示せば十分です．したがって，次を示せば十分です．

• 連結成分が孤立点ひとつといくつかの \(P_2\) であるようなグラフにおいて A が勝つことができる．

孤立点ひとつから始めて帰納法で示すことを考えると，次を示せばよいです．

• グラフ \(G\) でゲームした場合に A が勝てるならば，\(G\) に \(P_2\) を追加したグラフでゲームした場合にも A が勝てる．

追加した頂点を \(x,y\) として，A は，B が \(x,y\) のどちらかを選んだらその直後にもう一方を選ぶようにして，それ以外は \(G\) での必勝手順を再現するようにしていけばよいです．ただし B が一度も \(x,y\) を選ぶことなく A の手番で残り \(2\) 頂点になった場合には，A, B の順に \(x,y\) が選ばれるようにすればよいです．これで [A1] が示されました．

[B1] を示します．B が勝てることを示すためには，必要なら辺を減らした上で B が勝てることを示せば十分です．したがって，次を示せば十分です．

• 連結成分が \(P_3\) ひとつと孤立点偶数個であるようなグラフにおいて B が勝つことができる．

\(P_3\) から始めて帰納法で示すことを考えると，次を示せばよいです．

• グラフ \(G\) でゲームした場合に B が勝てるならば，\(G\) に孤立点を \(2\) つ追加したグラフでゲームした場合にも B が勝てる．

これは [A1] で証明したのと全く同じように証明できます．

以上により \(N\) が奇数の場合の議論が完成しました．

---

[2] \(N\) が偶数

• [B2] \(N\) が偶数で \(G\) が頂点を共有しない \(2\) つの \(P_3\) を部分グラフとして含むならば，B が勝てる．
• [B3] \(N\) が偶数で \(G\) が \(C_4\) を部分グラフとして含むならば，B が勝てる．
• [B4] \(N\) が偶数で \(G\) が \(C_3\) の各頂点に葉をつけたグラフ（下図の最右のグラフ）を含むならば，B が勝てる．

このことは，やはり [1] と同様の帰納法で証明できます（孤立点を \(2\) 頂点追加しても勝てることを示せるので，base step を適当な場合分けで確認すればよいです）．

以下では [B2], [B3], [B4] が成り立たないという仮定のもと，A が勝てることを証明します．特に [B2] が成り立たないことにより，頂点数 \(3\) 以上の連結成分は高々ひとつであることに注意します．

次数 \(3\) 以上の頂点の個数で場合分けします．

[2-1] 次数 \(3\) 以上の頂点が \(0\) 個

この場合，頂点数 \(3\) 以上の連結成分はパスまたはサイクルです．[B2], [B3] が成り立たないという条件下で，この成分は \(P_3, P_4, P_5, C_3, C_5\) のどれかです．よって次を示せば十分です．

• [A2] \(N\) が偶数で，\(G\) のすべての連結成分の頂点数が \(2\) 以下ならば，A が勝てる．
• [A3] \(N\) が偶数で，\(G\) の頂点数 \(3\) 以上の連結成分は唯一であり，それが \(P_3, P_4, P_5, C_3, C_5\) のいずれかならば A が勝てる．

やはり，[A1] を示したときと同様の証明で証明できます．

[2-2] 次数 \(3\) 以上の頂点が \(1\) 個

この次数 \(3\) 以上の頂点を \(v\) とすると，\(G-v\) の連結成分はすべて孤立点またはパスです．[B2], [B3] が成り立たないという仮定から，次を示せば十分です．

• [A4] \(N\) が偶数で，\(G\) は唯一の次数 \(3\) 以上の頂点を持ち，その頂点を \(v\) としたとき \(G-v\) の連結成分はすべて頂点数 \(2\) 以下だとする．このとき A が勝てる．

A は，「\(v\) を選んではならない」というルールを追加しても勝てることを証明します．このルールを追加することで，\(v\) に接続する辺は無視できます．適当に辺を追加すると，次を示せばよいことになります：

• 特殊な頂点 \(v\)，孤立点ひとつ，\(P_2\) いくつかからなるグラフで，「A は \(v\) を選んではならない」というルールを追加してゲームをした場合に，A が勝てる．

この場合にもやはり \(P_2\) の追加が A の勝利を保つことが言えるので，帰納法で証明できます．

[2-3] 次数 \(3\) 以上の頂点が \(2\) 個以上ある場合

[B2], [B3] が成り立たないという条件のもと，次数 \(3\) 以上の頂点はちょうど \(2\) つあり，次数はちょうど \(3\) であり，これらは隣接し，ちょうどひとつの近傍を共有することが分かります．つまり \(G\) は次のグラフを部分グラフとして含みます．

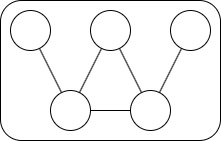
さらに [B4] も成り立たないならば，この連結成分に他の辺や頂点は存在しないことがいえます．よってこれまで議論していないのは次の場合だけです．

• [A5] \(N\) が偶数で，\(G\) の連結成分のひとつは上図のグラフであり，それ以外の連結成分は孤立点および \(P_2\) だけであるとき，A が勝てる．

これもこれまでと同様の帰納法で証明できます．

---

[3] まとめ

A の勝利条件は [A1], [A2], [A3], [A4], [A5] です．B の勝利条件は [B1], [B2], [B3], [B4] です．これまでの議論より，これらで場合分けは尽くされています．一方の勝利条件を適切に実装すれば，\(O(N+M)\) 時間で本問を解くことができます．

なお，適当な小さいグラフに対しては全探索することで実装や考察を簡略化することもできます．例えば [2-3] のケースで [B2] が成り立たない場合には連結成分の頂点数が適当な定数以下であることが証明できるので，そのような場合に全探索を行うような解法をとれば [B4] や [A5] を発見したり実装する必要はありません．