 /
/ 
Time Limit: 2 sec / Memory Limit: 1024 MiB
配点 : 600 点
問題文
頂点に 1 から N までの番号がついた N 頂点の根付き木が与えられます。頂点 1 が根で、頂点 i (2 \le i \le N) の親は頂点 p_i (1\le p_i < i) です。はじめ、全ての頂点は白で塗られています。
あなたは以下の一連の操作を 0 回以上何回でも行うことができます。
- 以下の条件を全て満たす整数の組 (u,v) を選ぶ。
- 1\le u < v \le N
- 頂点 u と頂点 v はどちらも白で塗られている。
- u は v の祖先 ではない。
- 頂点 u と頂点 v を黒で塗る。
ただし、「u は v の祖先ではない」とは頂点 v から今いる頂点の親に移動する操作を何回行っても頂点 u に到達できないことを意味します。
あなたが適切な順序で操作を行ったとき、最大で何回操作ができるか求めてください。
T 個のテストケースが与えられるので、それぞれについて答えを求めてください。
制約
- 1\le T\le 5\times 10^4
- 2\le N\le 5\times 10^5
- 1\le p_i < i
- 全てのテストケースにおける N の総和は 5\times 10^5 以下
- 入力される値は全て整数
入力
入力は以下の形式で標準入力から与えられる。
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
各テストケース \text{case}_i は以下の形式で与えられる。
N p_2 p_3 \ldots p_N
出力
T 行出力せよ。
i 行目 (1\le i\le T) には i 番目のテストケースについての答えを出力せよ。
入力例 1
4 6 1 2 2 2 5 7 1 2 3 4 5 6 7 1 2 3 4 2 4 12 1 1 2 2 2 4 4 4 7 7 7
出力例 1
2 0 2 5
1 番目のテストケースについて考えます。
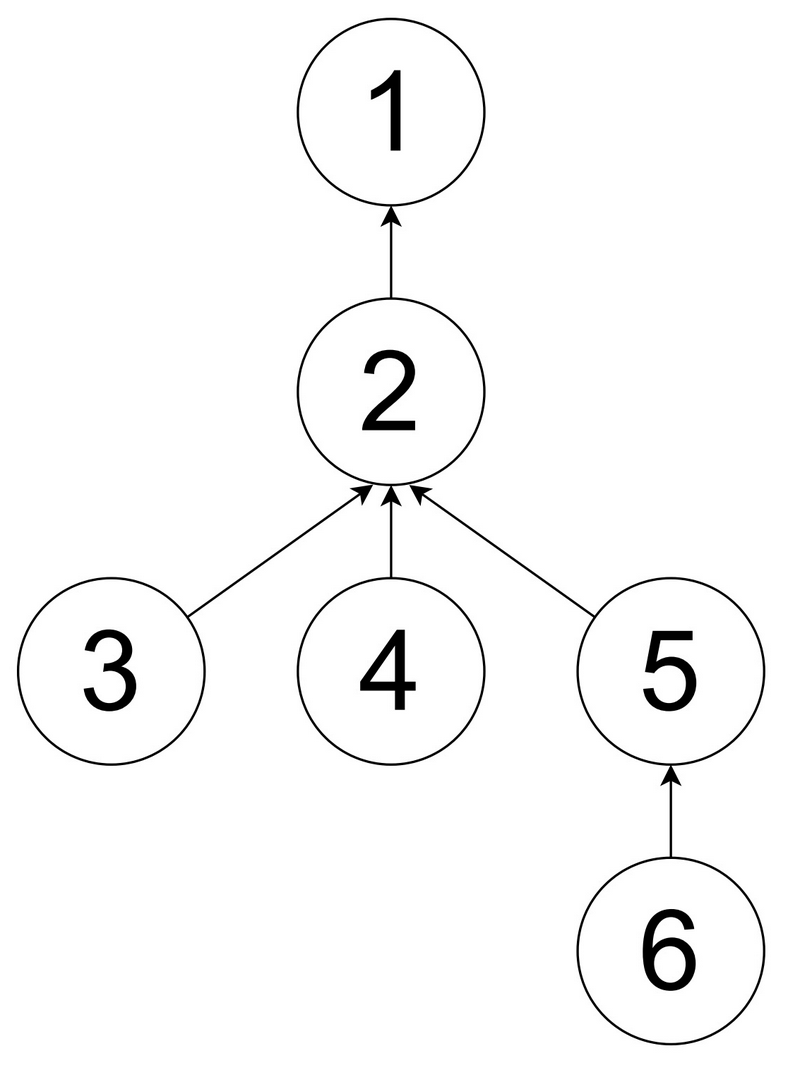
以下のように 2 回操作を行うことができます。
- (u,v)=(3,5) を選ぶ。頂点 3 と頂点 5 を黒で塗る。
- (u,v)=(4,6) を選ぶ。頂点 4 と頂点 6 を黒で塗る。
操作を 2 回より多く行うことはできないので、 1 行目には 2 を出力してください。
Score : 600 points
Problem Statement
You are given a rooted tree with N vertices numbered from 1 to N. Vertex 1 is the root, and the parent of vertex i (2 \le i \le N) is vertex p_i (1\le p_i < i). Initially, all vertices are colored white.
You can perform the following sequence of operations zero or more times.
- Choose a pair of integers (u,v) that satisfies all of the following conditions.
- 1\le u < v \le N
- Both vertices u and v are colored white.
- u is not an ancestor of v.
- Color vertices u and v black.
Here, "u is not an ancestor of v" means that you cannot reach vertex u from vertex v no matter how many times you perform the operation of moving to the parent of the current vertex.
Find the maximum number of operations you can perform when you perform operations in an appropriate order.
You are given T test cases, so find the answer for each of them.
Constraints
- 1\le T\le 5\times 10^4
- 2\le N\le 5\times 10^5
- 1\le p_i < i
- The sum of N over all test cases is at most 5\times 10^5.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
T
\text{case}_1
\text{case}_2
\vdots
\text{case}_T
Each test case \text{case}_i is given in the following format:
N p_2 p_3 \ldots p_N
Output
Output T lines.
The i-th line (1\le i\le T) should contain the answer for the i-th test case.
Sample Input 1
4 6 1 2 2 2 5 7 1 2 3 4 5 6 7 1 2 3 4 2 4 12 1 1 2 2 2 4 4 4 7 7 7
Sample Output 1
2 0 2 5
Consider the first test case.

You can perform two operations as follows.
- Choose (u,v)=(3,5). Color vertices 3 and 5 black.
- Choose (u,v)=(4,6). Color vertices 4 and 6 black.
You cannot perform more than two operations, so output 2 on the first line.