Let \(X\) be the number of indices \(i\) such that \(\min(B_i, B_{P_i}) = 0\) and \(\max(B_i, B_{P_i}) = 1\), and let \(Y\) be the number of indices \(i\) such that \(\max(B_i, B_{P_i}) = 0\). Then the score of \(B\) is \(2A_0 + X - Y\).

Since \(A_0\) is fixed for each query, this becomes a problem of maximizing \(X - Y\) where \(X\) and \(Y\) are defined as above.

Consider constructing \(B\) by initializing all elements to \(2\), changing \(A_0\) elements to \(0\), and then changing \(A_1\) elements that are \(2\) to \(1\).

In this case, regardless of the value of \(A_1\), we can decide which positions to change to \(0\) based only on the value of \(A_0\).

When \(A_0\) is fixed and we decide which positions to change to \(0\), let \(C[2]_{A_0}\) be the number of positions where changing \(2\) to \(1\) increases \(X\) by \(2\), let \(C[1]_{A_0}\) be the number of positions where it increases \(X\) by \(1\), and let \(Y_{A_0}\) be the number of positions where \(\max(B_i, B_{P_i}) = 0\).

A modification method is optimal if its \(Y_{A_0}\) is not larger than other methods and its \(C[2]_{A_0} - Y_{A_0}\) is not smaller. Such an optimal modification method exists for any \(A_0\).

Specifically, we should continue modifications in the following order until the number of \(0\)s becomes \(A_0\):

1. For even cycles, change at most half the size by skipping every other element to \(0\). The order of cycles to modify is arbitrary, but if possible, fill so that only cycles containing only \(2\)s and cycles where exactly half the cycle size is \(0\) remain.
2. For odd cycles, change half the size (rounded down) by skipping every other element to \(0\). Modify in order of decreasing cycle size.
3. For odd cycles of size not equal to \(1\), select one \(2\) that is adjacent to a \(2\) and change it to \(0\).
4. Select cycles of size \(1\) and change them to \(0\).
5. Change the remaining \(2\)s to \(0\) in any order.

For example, when modifying a cycle of size \(6\) in step 1:

2 - 2 - 2 - 2 - 2 - 2
2 - 0 - 2 - 2 - 2 - 2
2 - 0 - 2 - 0 - 2 - 2
2 - 0 - 2 - 0 - 2 - 0

For example, when modifying a cycle of size \(7\) in step 2:

2 - 2 - 2 - 2 - 2 - 2 - 2
2 - 0 - 2 - 2 - 2 - 2 - 2
2 - 0 - 2 - 0 - 2 - 2 - 2
2 - 0 - 2 - 0 - 2 - 0 - 2

If we know \(C[2]_{A_0}\), \(C[1]_{A_0}\), and \(Y_{A_0}\) for any \(A_0\), we can process queries in \(O(1)\) time, so our goal is to find these values.

Let \(G\) be a graph with \(N\) vertices and \(N\) edges \((i, P_i)\), and let \(S = (S_1, S_2, \ldots, S_{|S|})\) be the sequence of sizes of each connected component. Let \(S_{even}\) be the sequence of even elements from \(S\), and let \(S_{odd}\) be the sequence of odd elements \(\geq 3\) from \(S\) arranged in descending order. Let \(K\) be the number of \(1\)s.

We find the answer by case analysis based on the value of \(A_0\).

---

When \(0 \leq A_0 \leq \dfrac{\sum S_{even}}{2}\)

If there exists a subsequence \(T\) of \(S_{even}\) such that \(A_0 = \dfrac{\sum T}{2}\), then \((C[2]_{A_0}, C[1]_{A_0}, Y_{A_0}) = (A_0, 0, 0)\).

This can be achieved by arranging cycles of sizes included in \(T\) alternately as \((0, 2, 0, 2, \ldots)\).

If such a \(T\) does not exist, then \((C[2]_{A_0}, C[1]_{A_0}, Y_{A_0}) = (A_0 - 1, 2, 0)\).

This can be done by filling even cycles with \((0, 2, \ldots, 0, 2)\) in order, and when we run out of \(0\)s, make it like \((0, 2, 0, 2, 2, 2, 2, \ldots)\).

---

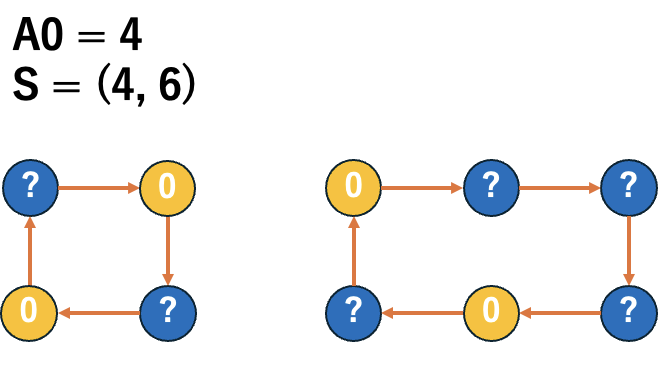
When \(\dfrac{\sum S_{even}}{2} < A_0 \leq \dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} - |S_{odd}|}{2}\)

Using the minimum \(k\) that satisfies \(A_0 - \dfrac{\sum S_{even}}{2} \leq \dfrac{\sum_{i=1}^k S_{odd}[i] - k}{2}\), we have \((C[2]_{A_0}, C[1]_{A_0}, Y_{A_0}) = (A_0 - k, 2k, 0)\).

This can be done by filling even cycles with \((0, 2, \ldots, 0, 2)\), then filling odd cycles with \((0, 2, 0, \ldots, 0, 2, 0)\) in order of decreasing size.

---

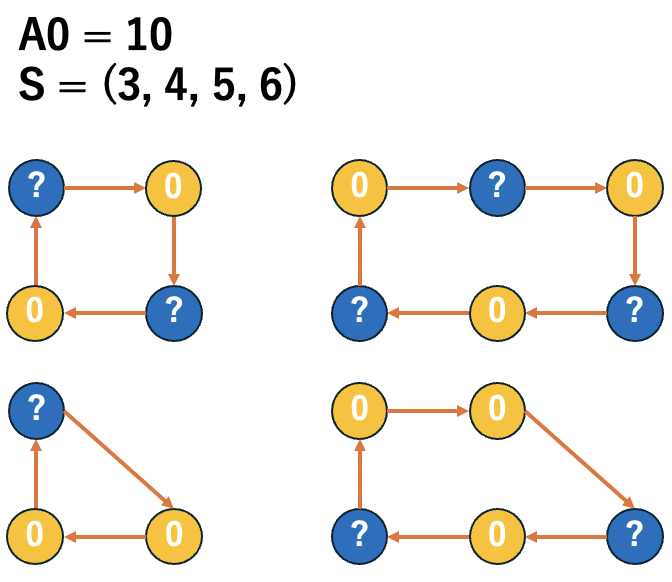
When \(\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} - |S_{odd}|}{2} < A_0 \leq \dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2}\)

Let \(r = A_0 - \dfrac{\sum S_{even}}{2} - \dfrac{\sum S_{odd} - |S_{odd}|}{2}\), then \((C[2]_{A_0}, C[1]_{A_0}, Y_{A_0}) = (A_0 - |S_{odd}|, 2(|S_{odd}| - r), r)\).

For example, when \(S_i = 5\), this can be done by changing what was filled as \((2, 0, 2, 0, 2)\) to \((0, 2, 0, 2, 0)\) for each element of \(S_{odd}\).

---

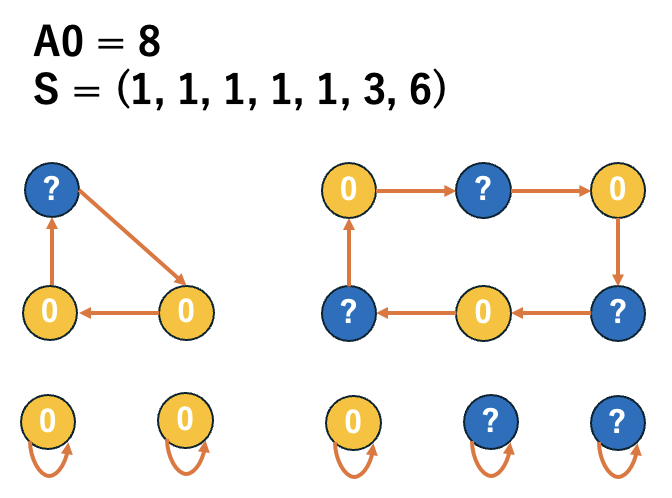
When \(\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2} < A_0 \leq \dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2} + K\)

\((C[2]_{A_0}, C[1]_{A_0}, Y_{A_0}) = (\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} - |S_{odd}|}{2}, 0, A_0 - \dfrac{\sum S_{even}}{2} - \dfrac{\sum S_{odd} - |S_{odd}|}{2})\).

---

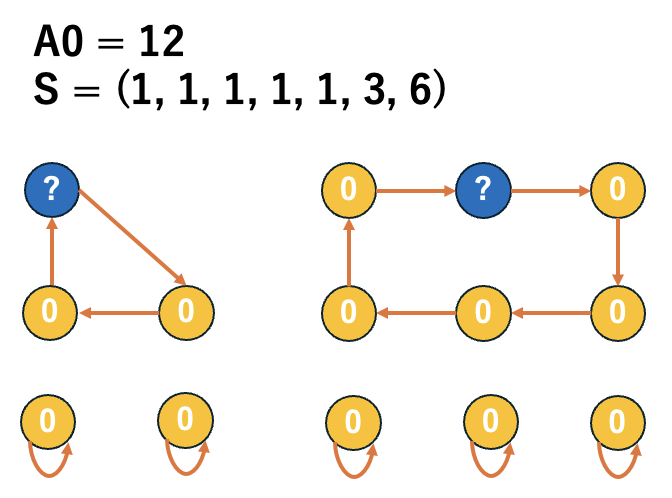
When \(\dfrac{\sum S_{even}}{2} + \dfrac{\sum S_{odd} + |S_{odd}|}{2} + K < A_0 \leq N\)

\((C[2]_{A_0}, C[1]_{A_0}, Y_{A_0}) = (N - A_0, 0, 2A_0 - N)\).

---

The above gives \((C[2]_{A_0}, C[1]_{A_0}, Y_{A_0})\) for all \(A_0\) from \(0\) to \(N\). Except for the part that finds the answer when \(0 \leq A_0 \leq \dfrac{\sum S_{even}}{2}\), everything can be computed in linear time with respect to \(N\). The part for finding the answer when \(0 \leq A_0 \leq \dfrac{\sum S_{even}}{2}\) can be computed in \(O(N\sqrt{N})\) time complexity using the fact that the number of distinct values in \(S_{even}\) is \(O(\sqrt{N})\). (Further speedup is possible using bitsets.)

Implementation Examples

C++ Implementation

PyPy Implementation