We will call matrices obtainable by operations good matrices. First, let’s think about how to find the number of good matrices.

We generate good matrices using the following procedure:

• Prepare a sequence \(R\) of length \(H\) consisting of integers from \(0\) to \(W\), and a sequence \(C\) of length \(W\) consisting of integers from \(0\) to \(H\). For \(1\leq i\leq H,1\leq j\leq W\), set \(A_{i,j}=1\) if \(j\leq R_i\) or \(i\leq C_j\), otherwise set \(A_{i,j}=0\).

While there are generally multiple \(R,C\) that generate a certain good matrix \(A\), we consider the one where \(C\) is lexicographically largest among them, and furthermore \(R\) is lexicographically largest among those. We call \(R,C\) satisfying this relationship a wonderful relationship. There is a one-to-one correspondence between \(R,C\) in a wonderful relationship and good matrices \(A\). For \(R,C\) in a wonderful relationship and the \(A\) generated from them, the following holds:

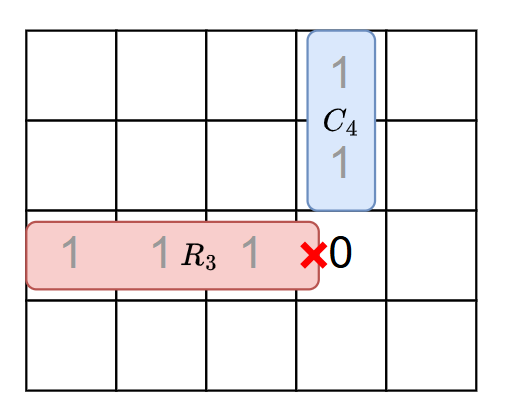
• When \(C_j\neq H\), we have \(A_{C_j+1,j}=0\). Therefore \(R_{C_{j}+1}\lt j\).
  
  • In the example below, since \(C_4=2\), we have \(A_{4,3}=0,R_3\lt 4\).

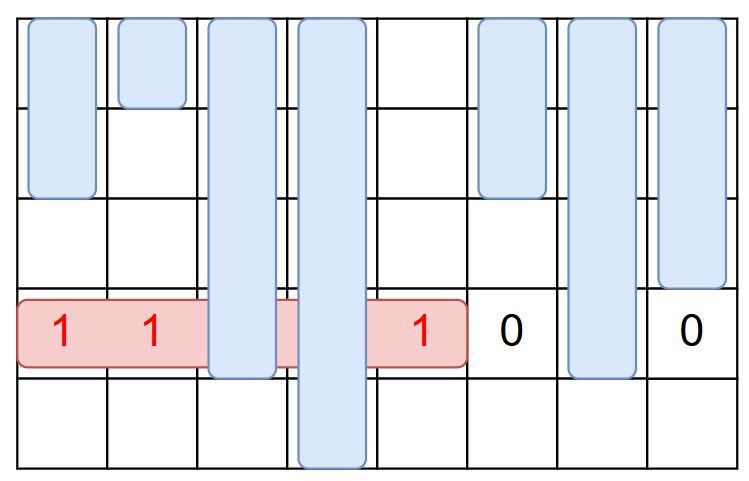
• Let \(j_1,j_2,\ldots\) be the \(j\) such that \(C_j\lt i\) in order. Then \(A_{i,j_1},A_{i,j_2},\ldots\) is monotonically decreasing.
  • In the example below, the \(j\) such that \(C_j\lt 4\) are \(j=1,2,5,6,8\), and we have \(A_{4,1}\geq A_{4,2}\geq A_{4,5}\geq A_{4,6}\geq A_{4,8}\).

Based on these observations, when \(C\) is determined, we can find the number of \(R\) that form a wonderful relationship with that \(C\). For \(R\) that form a wonderful relationship, the value of each \(R_i\) can be determined independently:

• Let \(L\) be the minimum \(j\) such that \(C_j=i-1\) (if it doesn’t exist, then \(L=W+1\)). Let \(d_i\) be the number of \(1\leq j\lt L\) such that \(A_j\lt i\). Then there are \(d_i+1\) ways to determine \(R_i\).

Based on the method for finding the number of \(R\) that form a wonderful relationship for each \(C\), we will find the total sum of the number of \(R\) that form a wonderful relationship for all \(C\). It’s good to classify this by focusing on the number of \(j\) such that \(C_j\lt i\).

When moving from row \(i\) to \(i+1\), suppose there exists \(j\) such that \(C_j=i\). What’s important is the relative relationship between such columns and the columns where \(C_j\lt i\). More specifically, the number of places where we can place \(1\) changes depending on where the columns with \(C_j=i\) are inserted among the columns with \(C_j\lt i\).

• The figure below shows how the number of places where we can place \(1\) (i.e., \(d_i\)) changes depending on the insertion position.

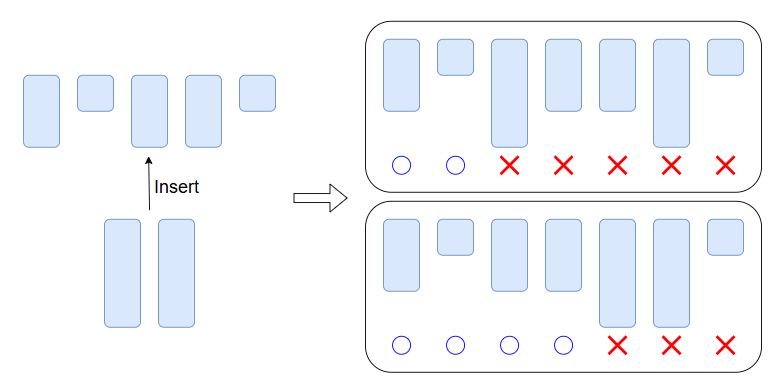
Depending on the position of the leftmost inserted column, we can freely decide:

• How far to the right we can extend \(1\)
• Where to insert the remaining columns to be inserted

We calculate this using DP. Let \(\mathrm{dp}[i][k]\) be the total number of ways to decide the following set:

• A subsequence \(C'\) (of length \(k\)) extracted from \(C\) consisting only of elements less than \(i\)
• For each row up to row \(i\), how many \(1\)s to extend from the left
  • This is, for \(i'=1,2,\ldots,i\), let \(L'\) be the minimum \(j\) such that \(C'_j=i'-1\) (if it doesn’t exist, then \(L'=k+1\)), and let \(d'_{i'}\) be the number of \(1\leq j\lt L'\) such that \(A_j\lt i'\). Then there are \(\prod_{i'=1}^i (d'_{i'}+1)\) ways.

When the number of \(j\) satisfying \(C_j\lt i\) is \(k_1\), and the number of \(j\) satisfying \(C_j\lt i+1\) is \(k_2\ (k_1\lt k_2)\), if we decide which position among the \(k_2\) positions to make the leftmost insertion (let the position be \(l\)), then there are degrees of freedom for:

• How far we can extend \(1\) from the left (\(l\) ways)
• Where to place the remaining \(k_2-k_1-1\) insertions among the \(k_2-l\) positions to the right of \(l\) (\(\binom{k_2-l}{k_2-k_1-1}\) ways)

Therefore, we follow the transition \(\displaystyle \mathrm{dp}[i+1][k_2]\leftarrow \mathrm{dp}[i][k_1]\times \sum_{l=1}^{k_2} l\times \binom{k_2-l}{k_2-k_1-1}=\mathrm{dp}[i][k_1]\times \binom{k_2+1}{k_1}\). (This transition formula is the same even when \(k_1=k_2\).) (You can also precompute the transition matrix in \(O(W^3)\) without transforming the binomial coefficient formula.)

Therefore, we can find \(\mathrm{dp}[H][\ast]\) in \(O(HW^2)\). Considering that when there exists \(j\) such that \(C_j=H\), we can decide where to insert those columns among the columns where \(C_j\lt H\), the final number of pairs \((R,C)\) where the wonderful relationship holds (i.e., the number of good matrices \(A\)) is \(\displaystyle \sum_{j=0}^W \mathrm{dp}[H][j]\times \binom{W}{j}\).

Using exactly the same approach, we can also find the total sum of \(\sum A_{i,j}\) over all good matrices.

When \(H<W\), we can swap \(H\) and \(W\), so we can solve this problem with time complexity \(O(HW\min(H,W))\) (it’s also possible to reduce it to \(O(HW\log \min(H,W))\) using convolution).

mod = 998244353
fac = [1] * 1000
for i in range(1, 1000):
    fac[i] = fac[i - 1] * i % mod
finv = [pow(fac[i], mod - 2, mod) for i in range(1000)]


def binom(n, k):
    if n < 0 or k < 0 or k > n:
        return 0
    return fac[n] * finv[k] % mod * finv[n - k] % mod


H, W = map(int, input().split())
if H < W:
    H, W = W, H

dp = [[0] * (W + 1) for i in range(H + 1)]
cnt = [[0] * (W + 1) for i in range(H + 1)]
dp[0][0] = 1
for i in range(H):
    for j in range(W + 1):
        for k in range(j, W + 1):
            dp[i + 1][k] = (dp[i + 1][k] + dp[i][j] * binom(k + 1, j)) % mod
            cnt[i + 1][k] = (cnt[i + 1][k] + cnt[i][j] * binom(k + 1, j) + dp[i][j] * binom(k + 1, j - 1)) % mod
        cnt[i + 1][j] = (cnt[i + 1][j] + dp[i + 1][j] * (W - j)) % mod
print(sum(cnt[H][i] * binom(W, i) % mod for i in range(W + 1)) % mod)

---

(Behind-the-scenes story of problem creation)

This problem was created when several people including myself and sotanishy visited Chichibu in Saitama Prefecture, and sotanishy, looking at the limestone mountain surface visible from Chichibu Station, said “I wonder if we could create a problem about carving rectangular grids.” The problem name comes from this episode.