Hints: https://atcoder.jp/contests/arc197/editorial/12878

[1] Observing the graph defined by the ancestor-descendant relation

Interpret the input matrix \(A\) as the adjacency matrix of an undirected graph: for \(i\neq j\), connect \(i\) and \(j\) if \(A_{i,j}=1\).

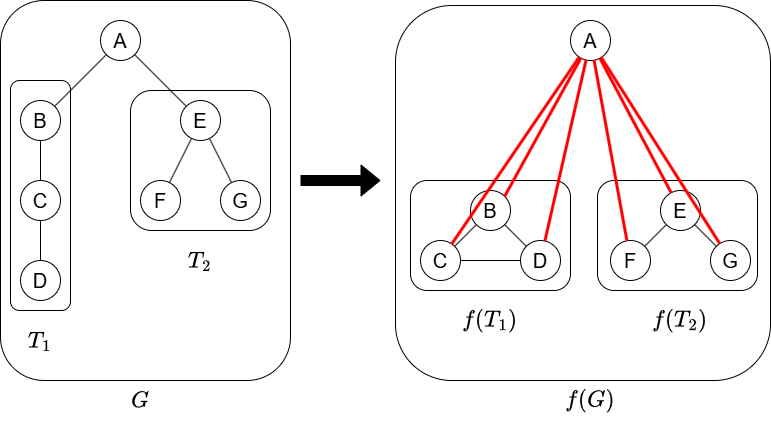
For a rooted tree \(G\), let \(f(G)\) be the graph formed by connecting every pair of vertices in an ancestor-descendant relation (excluding loops).

If \(G\) has root \(r\) with subtrees \(T_1,\dots,T_k\) attached, then \(f(G)\) can be constructed as follows:

• Find \(f(T_1),\dots,f(T_k)\). Then, connect \(r\) to every vertex in these subtrees.

[2] Counting

Given only \(f(G)\), how to reconstruct \(G\)? It can be done by reversing the above process:

• Choose as the root a vertex adjacent to all others.
• Remove that vertex and decompose the remaining graph into connected components. For each of them, reconstruct the rooted tree \(T_k\), and attach it to the root.

Here, there can be multiple choices for the root (if there is no choice, the answer is \(0\)). If there are multiple such vertices, the choice from those vertices does not affect the subsequent computation, so we can multiply the answer by the number of candidates and perform the recursive computation for some specific choice.

Alternatively, you can multiply the answer by the factorial of the number of candidates, and then remove all the candidates.

Note that in the very first step, we must choose vertex \(1\).

By implementing this method, the answer can be found in \(O(N^3)\) time (for example).

• Sample implementation: https://atcoder.jp/contests/arc197/submissions/65381404