 /
/ 
実行時間制限: 2 sec / メモリ制限: 1024 MiB
配点 : 700 点
問題文
H 行 W 列のグリッドがあります。 行には上から順に 0,1,\ldots, H-1 の番号が、列には左から順に 0,1,\ldots,W-1 の番号がついています。 行 i、列 j のマスをマス (i,j) と表すことにします。
H 個の文字列 S_0, S_1, \ldots, S_{H-1} が与えられます。それぞれの文字列は A と B のみからなる長さ W の文字列です。
各マスには、以下の 2 種類のタイルのいずれかを配置します。S_i の j+1 文字目 (0\leq j \leq W-1) を S_{ij} としたとき、マス (i,j) に配置するタイルの種類は S_{ij} です。
- 種類 A:タイルの表面に、隣接する 2 辺の中点どうしを結ぶ線分が一本描かれている

- 種類 B:タイルの表面に、向かい合う 2 辺の中点どうしを結ぶ線分が一本描かれている

タイルは自由に回転可能です。タイルの表面に描かれた線分のみに注目したとき、種類 A のタイルを回転する方法は 4 通り、種類 B のタイルを回転する方法は 2 通りあります。よって、線分が作る模様のみによってタイルの配置方法を区別したとき、タイルを配置する方法の数は、種類 A のタイルの数 a、種類 B のタイルの数 b を用いて、 4^a\times 2^b 通りと表されます。
このうち、グリッドをトーラスとして見たときにタイルに描かれた線分が行き止まりを持たないようにタイルを配置する方法の数を 998244353 で割ったあまりを出力してください。
ここで、グリッドをトーラスとして見たときにタイルに描かれた線分が行き止まりを持たないとは、具体的には、すべてのマス (i,j) について以下の 2 条件をともに満たすことを言います。
- 次の 2 つが、両方とも存在する、あるいはどちらも存在しない。
- マス (i,j) のタイルの右辺の中点を端点とする、マス (i,j) のタイルの表面に描かれた線分
- マス (i,(j+1)\bmod W) のタイルの左辺の中点を端点とする、マス (i,(j+1)\bmod W) のタイルの表面に描かれた線分
- 次の 2 つが、両方とも存在する、あるいはどちらも存在しない。
- マス (i,j) のタイルの下辺の中点を端点とする、マス (i,j) のタイルの表面に描かれた線分
- マス ((i+1)\bmod H,j) のタイルの上辺の中点を端点とする、マス ((i+1)\bmod H,j) のタイルの表面に描かれた線分
例えば、次の配置方法は条件を満たします。
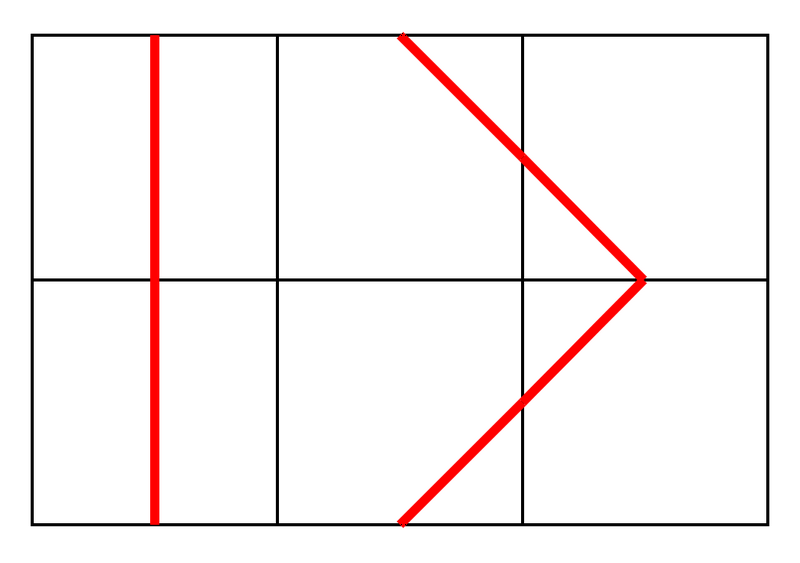
次の配置方法は条件を満たしません。具体的には、マス (0,2) のタイルの右辺の中点を端点とする線分が存在しないのに対し、マス (0,0) のタイルの左辺の中点を端点とする線分は存在するので、条件を満たしません。
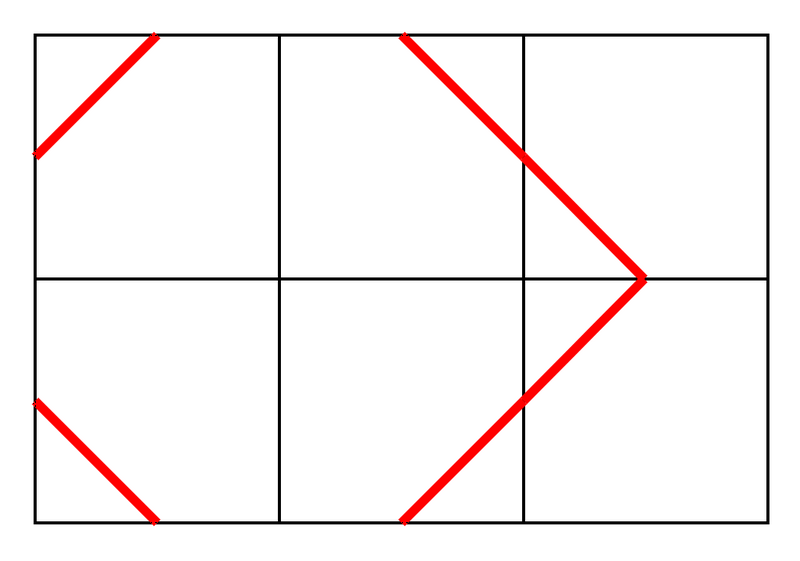
T 個のテストケースが与えられるので、それぞれについて解いてください。
制約
- 1 \le T \le 10^5
- 2 \le H,W
- HW\leq 10^6
- S_i\,(0\le i\le H-1) は
AとBのみからなる長さ W の文字列 - すべてのテストケースにわたる HW の総和は 10^6 以下
- T, H, W は整数
入力
入力は以下の形式で標準入力から与えられる。
T case_1 case_2 \vdots case_T
各ケースは以下の形式で与えられる。
H W
S_0
S_1
\vdots
S_{H-1}
出力
各テストケースに対する、問題文中の条件を満たすタイルの配置方法の数を 998244353 で割ったあまりを改行区切りで出力せよ。
入力例 1
3 3 3 AAB AAB BBB 3 3 BBA ABA AAB 3 4 BAAB BABA BBAA
出力例 1
2 0 2
1 番目のテストケースにおける正しい配置の一つの例として、以下の画像のようにタイルを配置する方法があります。
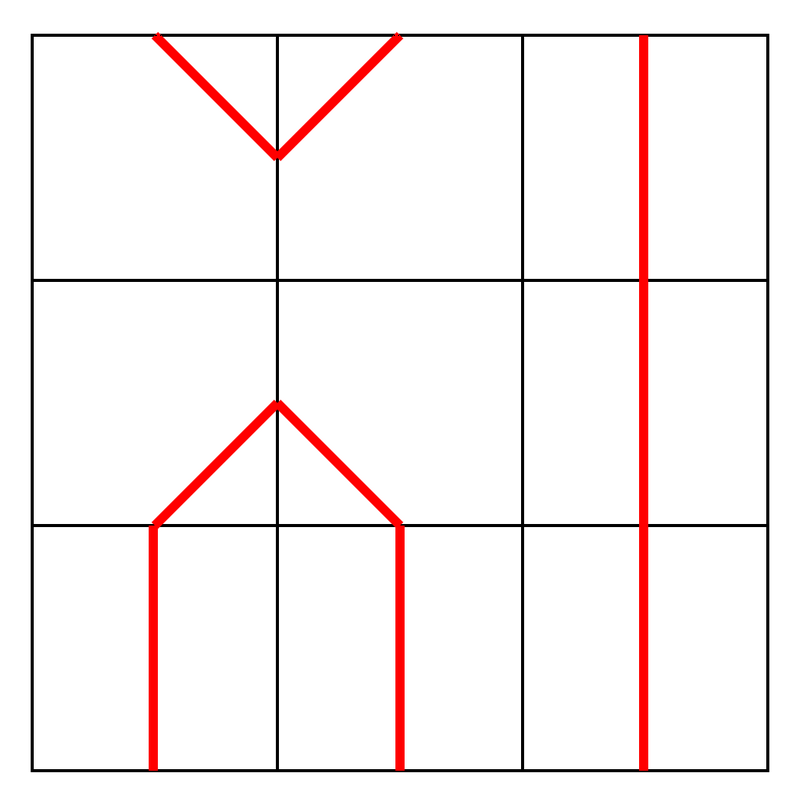
Score : 700 points
Problem Statement
There is a grid of H rows and W columns. The rows are numbered 0,1,\ldots,H-1 from top to bottom, and the columns are numbered 0,1,\ldots,W-1 from left to right. Let (i,j) denote the cell at row i and column j.
You are given H strings S_0, S_1, \ldots, S_{H-1}, each of which is of length W and consists of A and B.
In each cell, one of the following two types of tiles is placed. Let S_{ij} denote the (j+1)-th character (0 \le j \le W-1) of the string S_i. The type of tile placed in cell (i,j) is S_{ij}.
- Type A: A single line segment is drawn on the tile’s surface, connecting the midpoints of two adjacent edges.

- Type B: A single line segment is drawn on the tile’s surface, connecting the midpoints of two opposite edges.

These tiles can be freely rotated. When focusing only on the pattern formed by the line segments, there are four ways to rotate a Type-A tile and two ways to rotate a Type-B tile. Therefore, if we distinguish placements only by the pattern of line segments, the number of ways to place the tiles is 4^a \times 2^b, where a is the number of Type-A tiles and b is the number of Type-B tiles.
Among these ways, print the number, modulo 998244353, of ways such that the line segments on the tiles have no dead ends when viewing the grid as a torus.
Here, "the line segments on the tiles have no dead ends when viewing the grid as a torus" if and only if the following two conditions are satisfied for every cell (i,j):
- Both of the following exist, or neither of the following exists:
- the line segment drawn in the cell (i,j), whose endpoint is the midpoint of the right edge of the cell (i,j)
- the line segment drawn in the cell (i,(j+1)\bmod W), whose endpoint is the midpoint of the left edge of the cell (i,(j+1)\bmod W)
- Both of the following exist, or neither of the following exists:
- the line segment drawn in the cell (i,j), whose endpoint is the midpoint of the bottom edge of the cell (i,j)
- the line segment drawn in the cell ((i+1)\bmod H,j), whose endpoint is the midpoint of the top edge of the cell ((i+1)\bmod H,j)
For example, the following placement satisfies the condition:

The following placement does not satisfy the condition. Specifically, while there is no line segment whose endpoint is the midpoint of the right edge of the tile in cell (0,2), there is a line segment whose endpoint is the midpoint of the left edge of the tile in cell (0,0), so the condition is not satisfied.

You are given T test cases; solve each of them.
Constraints
- 1 \le T \le 10^5
- 2 \le H,W
- HW\leq 10^6
- S_i\,(0\le i\le H-1) are length-W strings consisting of
AandB. - The sum of H W over all test cases is at most 10^6.
- T, H, and W are integers.
Input
The input is given from Standard Input in the following format:
T case_1 case_2 \vdots case_T
Each case is given in the following format:
H W
S_0
S_1
\vdots
S_{H-1}
Output
For each test case, print the number, modulo 998244353, of placements that satisfies the condition, in separate lines.
Sample Input 1
3 3 3 AAB AAB BBB 3 3 BBA ABA AAB 3 4 BAAB BABA BBAA
Sample Output 1
2 0 2
One valid placement for the first test case is shown in the following image:
