\(A_{1}\leq A_{2}\) としても一般性を失わないので、これを仮定します。

この問題の答えは、以下の条件を全て満たす正の整数の組 \((X_{1}, X_{2})\) の場合の数と同じです。

• \(10 ^ {A_{1} - 1}\leq X_{1} < 10 ^ {A_{1}}\)
• \(10 ^ {A_{2} - 1}\leq X_{2} < 10 ^ {A_{2}}\)
• \(10 ^ {A_{3} - 1}\leq X_{1} + X_{2} < 10 ^ {A_{3}}\)

\(A_{1}\) 桁の正の数 \(X_{1}\) と \(A_{2}\) 桁の正の数 \(X_{2}\) の和は \(A_{2}\) 桁の正の数もしくは \(A_{2} + 1\) 桁の正の数になるので \(A_{3}\) が \(A_{2}, A_{2} + 1\) のいずれでもないときは答えは \(0\) になります。

よって、\(A_{3} = A_{2}\) もしくは \(A_{2} + 1\) の \(2\) 通りのみ考えれば良いです。

\(A_{3} = A_{2}\) のとき

\(X_{1}\) が正であることから、条件は以下のように置き換えられます。

• \(10 ^ {A_{1} - 1}\leq X_{1} < 10 ^ {A_{1}}\)
• \(10 ^ {A_{2} - 1}\leq X_{2} < 10 ^ {A_{2}} - X_{1}\)

\(X_{1}\) を固定して考えることで、答えは以下の式で表されます。

\[\sum_{X_{1} = 10^{A_{1} - 1}}^{10^{A_{1}} - 1} \max(0, 9\times 10^{A_{2} - 1} - X_{1})\]

\(A_{1} = A_{2}\) のとき

上の図の左下の部分の面積を求めるイメージです。

\[\sum_{X_{1} = 10^{A_{1} - 1}}^{10^{A_{1}} - 1} \max(0, 9\times 10^{A_{2} - 1} - X_{1}) =\sum_{X_{1} = 10^{A_{2} - 1}}^{9\times 10^{A_{2} - 1} } (9\times 10^{A_{2} - 1} - X_{1}) = \dfrac{(8\times 10^{A_{1} - 1})(8\times 10^{A_{1} - 1} + 1)}{2}\]

\(A_{1} < A_{2}\) のとき

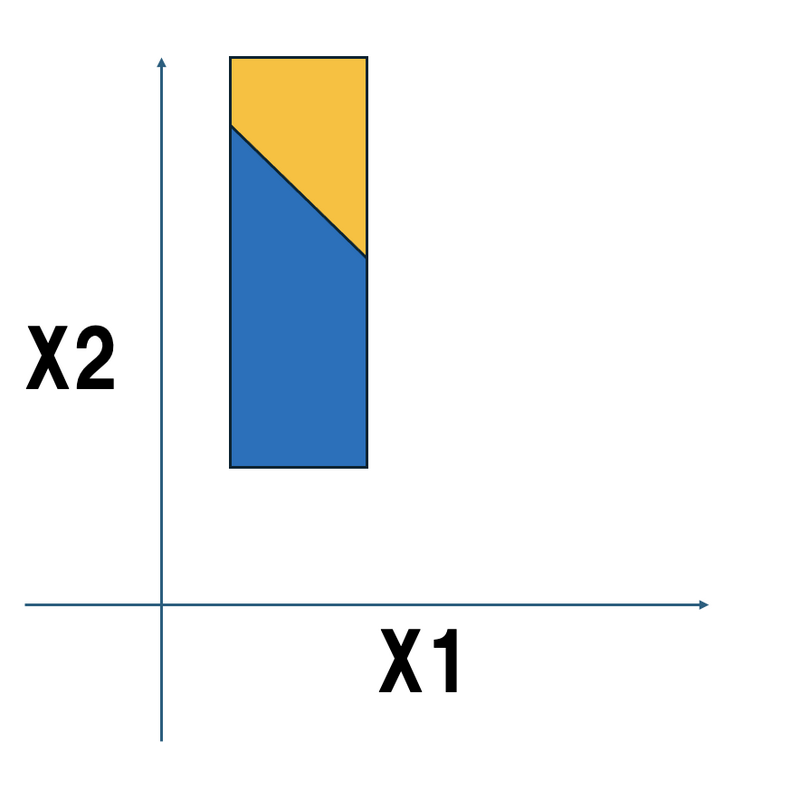
上の図の左下の部分の面積を求めるイメージです。(図形の大きさは実際とは異なります。)

\[\sum_{X_{1} = 10^{A_{1} - 1}}^{10^{A_{1}} - 1} \max(0, 9\times 10^{A_{2} - 1} - X_{1}) = \sum_{X_{1} = 10^{A_{1} - 1}}^{10^{A_{1}} - 1} (9\times 10^{A_{2} - 1} - X_{1}) = 9\times 10^{A_{1} - 1}\left(9\times 10^{A_{2} - 1} - \dfrac{10^{A_{1} - 1} + 10^{A_{1}} - 1}{2}\right)\]

この \(2\) つの値の \(998244353\) で割ったあまりは、時間計算量 \(O(\log(A_{2}))\) で計算できます。

\(A_{3} = A_{2} + 1\) のとき

\(A_{3} = A_{2}\) のときの答えを求め、\(81\times 10^{A_{1} + A_{2} - 2}\) からその値を引けば良いです。

以上より \(1\) つのテストケースについて、時間計算量 \(O(\log(A_{2}))\) で求まるので、全体の時間計算量は \(O(T\log(A_{2}))\) です。

c++ による実装例

python による実装例

MOD = 998244353

# return 10 ^ a
def powten(a):
    return pow(10, a, MOD)

def solve(a1, a2, a3):
    # a1 <= a2
    if a1 > a2:
        a1, a2 = a2, a1
    # impossible
    if a2 != a3 and a2 + 1 != a3:
        return 0
    # a2 == a3
    if a2 != a3:
        return (81 * powten(a1 + a2 - 2) - solve(a1, a2, a2)) % MOD
    # calc
    if a1 == a2:
        return 4 * powten(a1 - 1) * (8 * powten(a1 - 1) + 1) % MOD
    else:
        ans = (9 * powten(a2 - 1) - (11 * powten(a1 - 1) - 1) * pow(2, -1, MOD)) % MOD
        ans = ans * 9 * powten(a1 - 1) % MOD
        return ans
    

# I/O
T = int(input())
for _ in range(T):
    a1, a2, a3 = map(int,input().split())
    print(solve(a1, a2, a3))