Step 1

First, let’s consider what the optimal movement strategy might be.

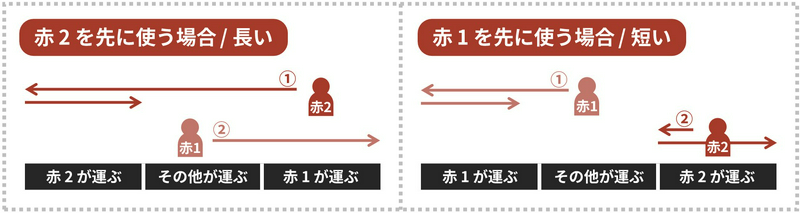
Let’s call the residents who have a coupon of company A, from west to east, as Blue \(1\), Blue \(2\), Blue \(3\), …, and those who have a coupon of company J as Red \(1\), Red \(2\), Red \(3\), … In this case, it is not optimal for a resident, say Red \(2\), to touch the luggage after Red \(1\) has already done so, as reversing the order of the same color, like from Red \(2\) to Red \(1\), would reduce the cost as shown in the figure below.

[The Japanese texts below mean the following. 赤 \(i\) を先に使う場合: The case Red \(i\) is used first, 長い: long, 短い: short, 赤 \(i\) が運ぶ: Red \(i\) carries, その他が運ぶ: others carry]

Using this property, a dynamic programming approach naturally comes to mind, maintaining the following four states and recording the current minimum cost:

• Current position: \(\mathrm{pos}\)
• How many of the Blue residents have been used up to now: \(b\)
• How many of the Red residents have been used up to now: \(r\)
• Which color, Blue or Red, is currently holding the luggage: \(\mathrm{type}\)

That is, a dynamic programming of the form \(\mathrm{dp}[\mathrm{pos}][b][r][\mathrm{type}] = (\text{minimum cost})\). However, it has \(O(N^3)\) states, which unfortunately leads to TLE under the constraints of this problem.

---

Step 2

Can we further reduce the number of states?

First, we can assume that Blue and Red residents who are more than two positions to the left of the current position will not touch the luggage. Specifically, if the number of Blue and Red residents to the left of position \(\mathrm{pos}\) are \(b_{\mathrm{left}}\) and \(r_{\mathrm{left}}\), respectively, we may assume \(b \geq b_{\mathrm{left}}, r \geq r_{\mathrm{left}}\) in \(\mathrm{dp}[\mathrm{pos}][b][r][\mathrm{type}]\).

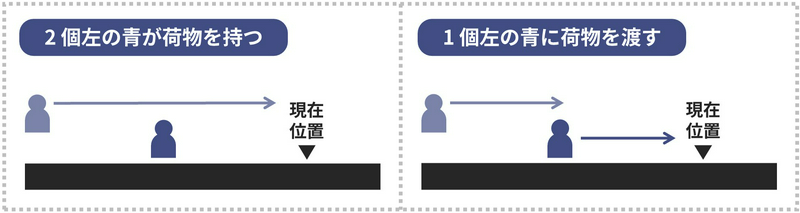
This is because, as shown in the figure below, letting a Blue resident who is two positions to the left touch the luggage, and passing the luggage to a Blue resident one position to the left when reaching that position, costs the same.

However, even with this improvement, the number of states remains \(O(N^3)\), which still leads to TLE.

[\(2\) 個左の青が荷物を持つ: The blue two positions to the left holds the luggage, \(1\) 個左の青に荷物を渡す: Pass the luggage to the blue one position to the left, 現在位置: current position]

---

Step 3

Can we further reduce the number of states?

In Step 2, we constrained the current position from the left, but it is also possible to constrain it from the right. Specifically, under the constraints of this problem, we may assume that Blue and Red residents who are more than \(20\) positions to the right of the current position will not touch the luggage. To be precise, if the number of Blue and Red residents to the left of position \(\mathrm{pos}\) are \(b_{\mathrm{left}}\) and \(r_{\mathrm{left}}\), respectively, we may assume \(b \leq b_{\mathrm{left}} + 20, r \leq r_{\mathrm{left}} + 20\) in \(\mathrm{dp}[\mathrm{pos}][b][r][\mathrm{type}]\).

---

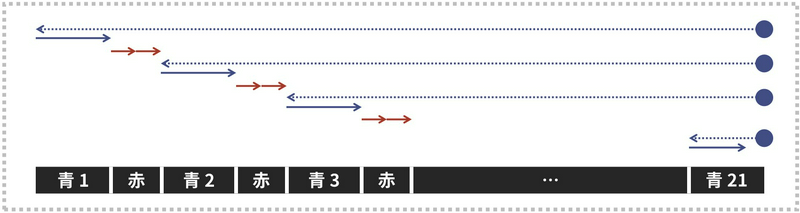
Why is this possible? Consider the following worst-case scenario which might not be constrainted by the upper limit of \(20\):

• Blue residents: None exist to the left of position \(L-1\), and \(21\) exist at position \(L\)
• Red residents: Exist everywhere

In this case, if \(21\) passes of the luggage to Blue residents occur as shown in the right figure, the upper limit of \(20\) cannot be maintained. The reason this is the worst case is intuitively because “the fewer Red residents there are, the more likely it is for one Blue to cover a long distance,” and “having Blue residents at position \(L\) rather than to the left of \(L-1\) makes it easier to earn the value of \(b - b_{\mathrm{left}}\) at the goal.”

Now, under the constraint \(L \leq 6 \times 10^4\), consider if such a scenario could occur.

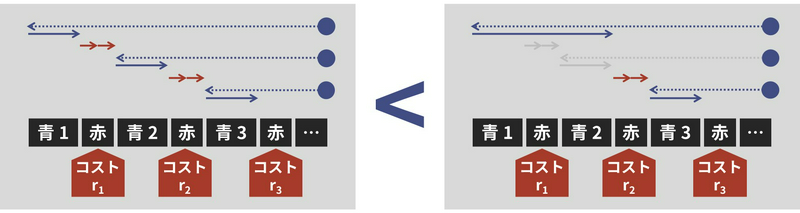
Let the number of Red (company J) planes included in the “Red carrying part” to the right of the places marked Blue \(1\), Blue \(2\), …, Blue \(20\) be \(r_1\), \(r_2\), \(\dots\), \(r_{20}\), respectively. Then, for the cost of (1) below to be less than (2), it must satisfy \(r_1 \geq r_2 + r_3 + \dots + r_{20}\).

1. As shown in the left figure below, the Blue \(1\) resident carries only in the place marked “Blue 1”
2. As shown in the right figure below, the Blue \(1\) resident carries up to the place marked “Blue 2”

[コスト: cost]

Also, for the cost of (1) below to be less than (2), it must satisfy \(r_2 \geq r_3 + r_4 + \dots + r_{20}\).

1. The Blue \(2\) resident carries only in the place marked “Blue \(3\)”
2. The Blue \(2\) resident carries up to the place marked “Blue \(4\)”

Furthermore, for the cost of (1) below to be less than (2), it must satisfy \(r_3 \geq r_4 + r_5 + \dots + r_{20}\). The same applies to \(r_4, r_5, \dots\).

1. The Blue \(3\) resident carries only in the place marked “Blue \(4\)”
2. The Blue \(3\) resident carries up to the place marked “Blue \(5\)”

And if \(r_{20} = 0\), it would be optimal for the Blue \(20\) resident to carry to the end, making the \(21\)-st person unnecessary, so \(r_{20} \geq 1\). Therefore, \(r_{19} \geq 1, r_{18} \geq 2, r_{17} \geq 4, \dots, r_1 \geq 2^{18}\), which contradicts the constraint \(L \leq 6 \times 10^4\).

Thus, it has been proven that it can be constrained to up to \(20\) positions to the right as well.

---

Sample Implementation (C++)

Below is a sample implementation in C++. Points to note in the implementation include:

• Be careful with the handling of multiple residents at the same position.
• Be careful managing memory with \(O(N^3)\) states, or you will get MLE.
• Don’t spend \(O(K)\) time for transitions where \(K = 20\), or you will get TLE.

#include <bits/stdc++.h>
using namespace std;

struct agent {
    int x; char c;
};

int GetCost(int stt, int goa, char col, vector<int> &SumA, vector<int> &SumJ) {
    if (stt > goa) swap(stt, goa);
    if (col == 'A') return SumJ[goa] - SumJ[stt];
    if (col == 'J') return SumA[goa] - SumA[stt];
    return -1;
}

int Solve(int L, int N, const string &S, const vector<agent>& A) {
    vector<vector<vector<vector<int>>>> dp(L + 5, vector<vector<vector<int>>>(22, vector<vector<int>>(22, vector<int>(3, (1 << 29)))));
    vector<int> CountA(L + 5, 0);
    vector<int> CountJ(L + 5, 0);
    vector<int> SumA(L + 5, 0);
    vector<int> SumJ(L + 5, 0);
    vector<int> ListA;
    vector<int> ListJ;

    // Step 1. Cumulative Sum 1
    for (int i = 0; i < N; i++) {
        if (A[i].c == 'A') { CountA[A[i].x + 1] += 1; ListA.push_back(A[i].x); }
        if (A[i].c == 'J') { CountJ[A[i].x + 1] += 1; ListJ.push_back(A[i].x); }
    }
    ListA.push_back(L + 1);
    ListJ.push_back(L + 1);
    for (int i = 0; i <= L + 2; i++) CountA[i + 1] += CountA[i];
    for (int i = 0; i <= L + 2; i++) CountJ[i + 1] += CountJ[i];
    sort(ListA.begin(), ListA.end());
    sort(ListJ.begin(), ListJ.end());

    // Step 2. Cumulative Sum 2
    for (int i = 0; i < L; i++) {
        if (S[i] == 'A') SumA[i + 1] += 1;
        if (S[i] == 'J') SumJ[i + 1] += 1;
    }
    for (int i = 0; i <= L; i++) SumA[i + 1] += SumA[i];
    for (int i = 0; i <= L; i++) SumJ[i + 1] += SumJ[i];
    SumA[L + 1] = (1 << 28);
    SumJ[L + 1] = (1 << 28);

    // Step 3. DP Init
    for (int i = 0; i <= L; i++) {
        for (int j = 0; j < 20; j++) {
            for (int k = 0; k < 20; k++) dp[i][j][k][0] = (1 << 29);
            for (int k = 0; k < 20; k++) dp[i][j][k][1] = (1 << 29);
            for (int k = 0; k < 20; k++) dp[i][j][k][2] = (1 << 29);
        }
    }
    dp[0][2][2][0] = 0;

    // Step 4. DP Main
    for (int i = 0; i < L; i++) {
        for (int j = 0; j < 20; j++) {
            for (int k = 0; k < 20; k++) {
                int IndexA = (j - 2) + CountA[i]; if (IndexA < 0 || IndexA >= ListA.size()) continue;
                int IndexJ = (k - 2) + CountJ[i]; if (IndexJ < 0 || IndexJ >= ListJ.size()) continue;

                // Transition
                int posA = max(0, IndexA - CountA[i + 1] + 2);
                int posJ = max(0, IndexJ - CountJ[i + 1] + 2);
                int cstA = GetCost(ListA[IndexA], i, 'A', SumA, SumJ);
                int cstJ = GetCost(ListJ[IndexJ], i, 'J', SumA, SumJ);

                // 0 -> *
                if (posA >= 1) dp[i + 1][posA][posJ][1] = min(dp[i + 1][posA][posJ][1], dp[i][j][k][0] + cstA + (S[i] == 'A' ? 0 : 1));
                if (posJ >= 1) dp[i + 1][posA][posJ][2] = min(dp[i + 1][posA][posJ][2], dp[i][j][k][0] + cstJ + (S[i] == 'J' ? 0 : 1));

                // * -> 0
                if (j + 1 < 20) dp[i][j + 1][k][0] = min(dp[i][j + 1][k][0], dp[i][j][k][1]);
                if (j + 1 < 20) dp[i][j + 1][k][0] = min(dp[i][j + 1][k][0], dp[i][j][k][0]);
                if (k + 1 < 20) dp[i][j][k + 1][0] = min(dp[i][j][k + 1][0], dp[i][j][k][2]);
                if (k + 1 < 20) dp[i][j][k + 1][0] = min(dp[i][j][k + 1][0], dp[i][j][k][0]);

                // * -> *
                dp[i + 1][posA][posJ][1] = min(dp[i + 1][posA][posJ][1], dp[i][j][k][1] + (S[i] == 'A' ? 0 : 1));
                dp[i + 1][posA][posJ][2] = min(dp[i + 1][posA][posJ][2], dp[i][j][k][2] + (S[i] == 'J' ? 0 : 1));
            }
        }
    }

    // Step 5. Finalize
    int Answer = (1 << 29);
    for (int i = 0; i < 20; i++) {
        for (int j = 0; j < 20; j++) {
            for (int k = 0; k < 3; k++) Answer = min(Answer, dp[L][i][j][k]);
        }
    }
    return Answer;
}

int main() {
    // Step 1. Input
    int L, N; string S;
    cin >> L >> N;
    cin >> S;
    vector<agent> A(N);
    for (int i = 0; i < N; i++) cin >> A[i].x >> A[i].c;
    cout << Solve(L, N, S, A) << endl;
    return 0;
}