E - Wrong Scoreboard Editorial by evima
Solution to the problem
In fact, there are only \(113\) scoring distributions for the contest, shown below, that need to be considered.
Moreover, once the scoring distribution is determined, if we arrange the penalties so that the smaller \(R_i\) values correspond to smaller penalties (within ties), the squared error will always be minimized. Therefore, by using something like std::sort, we can solve this in approximately \(113N \log N\) computations.
[1, 1, 1, 1, 1]
[1, 1, 1, 1, 2]
[1, 1, 1, 1, 3]
[1, 1, 1, 1, 4]
[1, 1, 1, 2, 2]
[1, 1, 1, 2, 3]
[1, 1, 1, 2, 4]
[1, 1, 1, 2, 5]
[1, 1, 1, 3, 3]
[1, 1, 1, 3, 4]
[1, 1, 1, 3, 5]
[1, 1, 1, 3, 6]
[1, 1, 2, 2, 2]
[1, 1, 2, 2, 3]
[1, 1, 2, 2, 4]
[1, 1, 2, 2, 5]
[1, 1, 2, 2, 6]
[1, 1, 2, 3, 3]
[1, 1, 2, 3, 4]
[1, 1, 2, 3, 5]
[1, 1, 2, 3, 6]
[1, 1, 2, 3, 7]
[1, 1, 2, 4, 4]
[1, 1, 2, 4, 5]
[1, 1, 2, 4, 6]
[1, 1, 2, 4, 7]
[1, 1, 2, 4, 8]
[1, 1, 3, 3, 4]
[1, 1, 3, 3, 5]
[1, 1, 3, 4, 5]
[1, 1, 3, 4, 6]
[1, 1, 3, 5, 6]
[1, 1, 3, 5, 7]
[1, 1, 4, 4, 6]
[1, 1, 4, 5, 7]
[1, 1, 4, 6, 8]
[1, 2, 2, 2, 3]
[1, 2, 2, 2, 5]
[1, 2, 2, 3, 3]
[1, 2, 2, 3, 4]
[1, 2, 2, 3, 5]
[1, 2, 2, 3, 6]
[1, 2, 2, 3, 7]
[1, 2, 2, 3, 8]
[1, 2, 2, 4, 5]
[1, 2, 2, 4, 7]
[1, 2, 2, 5, 6]
[1, 2, 2, 5, 8]
[1, 2, 3, 3, 4]
[1, 2, 3, 3, 5]
[1, 2, 3, 3, 7]
[1, 2, 3, 4, 4]
[1, 2, 3, 4, 5]
[1, 2, 3, 4, 6]
[1, 2, 3, 4, 7]
[1, 2, 3, 4, 8]
[1, 2, 3, 4, 9]
[1, 2, 3, 4, 10]
[1, 2, 3, 5, 6]
[1, 2, 3, 5, 7]
[1, 2, 3, 5, 9]
[1, 2, 3, 6, 7]
[1, 2, 3, 6, 8]
[1, 2, 3, 6, 10]
[1, 2, 4, 4, 5]
[1, 2, 4, 4, 7]
[1, 2, 4, 5, 6]
[1, 2, 4, 5, 7]
[1, 2, 4, 5, 8]
[1, 2, 4, 6, 7]
[1, 2, 4, 6, 9]
[1, 2, 4, 7, 8]
[1, 2, 4, 7, 10]
[1, 2, 5, 6, 8]
[1, 2, 5, 6, 9]
[1, 2, 6, 7, 10]
[1, 3, 3, 4, 5]
[1, 3, 3, 5, 7]
[1, 3, 4, 4, 6]
[1, 3, 4, 5, 6]
[1, 3, 4, 5, 7]
[1, 3, 4, 6, 8]
[1, 3, 4, 7, 9]
[1, 3, 4, 8, 10]
[1, 3, 5, 6, 7]
[1, 3, 5, 7, 9]
[1, 3, 6, 8, 10]
[1, 4, 5, 6, 8]
[2, 2, 2, 3, 3]
[2, 2, 3, 3, 4]
[2, 2, 3, 4, 5]
[2, 2, 3, 5, 6]
[2, 2, 3, 6, 7]
[2, 2, 3, 7, 8]
[2, 3, 3, 4, 4]
[2, 3, 3, 4, 5]
[2, 3, 3, 4, 8]
[2, 3, 4, 4, 5]
[2, 3, 4, 5, 6]
[2, 3, 4, 5, 8]
[2, 3, 4, 6, 7]
[2, 3, 4, 7, 8]
[2, 3, 4, 8, 9]
[2, 3, 4, 9, 10]
[2, 3, 5, 6, 7]
[2, 3, 6, 7, 8]
[2, 4, 5, 6, 7]
[2, 4, 5, 7, 8]
[2, 5, 6, 8, 9]
[3, 4, 4, 5, 6]
[3, 4, 5, 6, 7]
[3, 4, 5, 6, 8]
[4, 5, 6, 7, 8]
How to come up with the solution?
Now, how can we come up with the above solution? In the latter part of this explanation, I would like to discuss how to think of the solution, also serving as a proof.
Step 1
First, let’s consider what kind of scoring distributions we should investigate, using the following example:
- The contest has \(3\) problems.
- Contestant \(1\) solved problem \(1\).
- Contestant \(2\) solved problem \(3\).
- Contestant \(3\) solved problems \(1\) and \(2\).
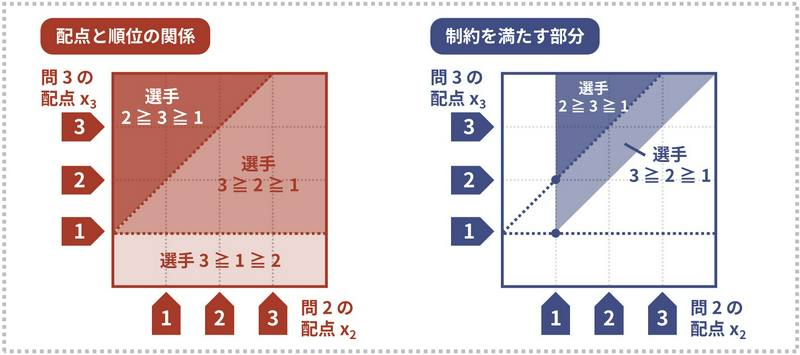
Let the scores for problems \(1\), \(2\), and \(3\) be \(x_1\), \(x_2\), and \(x_3\), respectively. As we vary \(x_1, x_2, x_3\), the rankings of the contestants change at the following moments:
- When \(x_3 = x_1\): The ranks of contestants \(1\) and \(2\) switch.
- When \(x_3 = x_1 + x_2\): The ranks of contestants \(2\) and \(3\) switch.
Therefore, assuming the score for problem \(1\) is \(1\) point, the relationship between scores and rankings can be represented as shown in the diagram on the left below. Moreover, reading the problem statement carefully, we see that the scores must be non-decreasing \((x_1 \leq x_2 \leq x_3)\). Thus, the part of the diagram that satisfies this constraint looks like the diagram on the right.
Since the ranks among contestants with the same total score can be freely swapped, we only need to investigate the boundaries of the regions, particularly the intersections. Therefore, in the example above, we only need to consider the following two scoring distributions:
- \((x_1, x_2, x_3) = (1, 1, 1)\)
- \((x_1, x_2, x_3) = (1, 1, 2)\)
[The Japanese texts below mean the following. 配点と順位の関係: relation between scores and ranks, 問 \(i\) の配点 \(x_i\): the score \(x_i\) of problem \(i\), 選手: contestants, 制約を満たす部分: the part satisfying the constraints]
Step 2
The considerations from Step 1 also apply when the contest has \(5\) problems. Specifically, the moments when the ranks of two contestants switch, as well as the constraint conditions \((1 =) \ x_1 \leq x_2 \leq x_3 \leq x_4 \leq x_5\), can be represented as several hyperplanes in a \(5\)-dimensional space. However, we only need to consider the points where four of these hyperplanes intersect. Note that we are assuming \(x_1 = 1\), as in Step 1.
Now, how many hyperplanes are there? The emerging hyperplanes are always represented by equations of the form \(a_1x_1 + a_2x_2 + a_3x_3 + a_4x_4 + a_5x_5 = 0\), where the values of \(a_1, a_2, a_3, a_4, a_5\) are \(-1\), \(0\), or \(+1\). Therefore, we only need to consider at most \(3^5 = 243\) hyperplanes. In reality, we do not need to consider those with all coefficients zero or those that are the same when signs are reversed, so there are only \(121\) hyperplanes to consider.
Thus, the number of scoring distributions to consider is narrowed down to at most \(C(121, 4) = 8495410\).
Step 3
With the considerations up to Step 2, we could solve this problem with approximately \(8495410 N \log N\) computations. However, given the constraint \(N \leq 3 \times 10^5\), this would unfortunately result in a TLE. So, let’s use the following idea:
- Among the \(8495410\) cases, aren’t there many with exactly the same scoring distribution?
Indeed, this idea is correct. For example, the following five “intersection points of four hyperplanes” all result in the same scoring distribution \((x_1, x_2, x_3, x_4, x_5) = (1, 1, 1, 1, 2)\):
- Intersection of hyperplanes \(x_1 = x_2, x_2 = x_3, x_3 = x_4, x_1 + x_2 = x_5\)
- Intersection of hyperplanes \(x_1 = x_2, x_2 = x_3, x_2 = x_4, x_1 + x_3 = x_5\)
- Intersection of hyperplanes \(x_1 = x_2, x_1 = x_3, x_3 = x_4, x_1 + x_4 = x_5\)
- Intersection of hyperplanes \(x_1 = x_3, x_2 = x_3, x_3 = x_4, x_2 + x_3 = x_5\)
- Intersection of hyperplanes \(x_1 = x_3, x_2 = x_4, x_3 = x_4, x_2 + x_4 = x_5\)
So, how many cases are there once duplicates and the ones without non-decreasing scores are removed? When checked with the following program, it turns out there are only \(113\) cases. Given the constraint \(N \leq 3 \times 10^5\), this allows us to achieve AC.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Point5D {
double x[5];
};
bool operator<(const Point5D& a1, const Point5D& a2) {
for (int i = 0; i < 5; i++) {
if (a2.x[i] - a1.x[i] > 1.0e-9) return true;
if (a1.x[i] - a2.x[i] > 1.0e-9) return false;
}
return false;
}
bool operator==(const Point5D& a1, const Point5D& a2) {
for (int i = 0; i < 5; i++) {
if (a2.x[i] - a1.x[i] > 1.0e-9) return false;
if (a1.x[i] - a2.x[i] > 1.0e-9) return false;
}
return true;
}
// Calculate the cross point of 5 hyperplanes (4 hyperplanes + x1=1)
// This program uses "Gauss-Jordan elimination algorithm"
Point5D GetCrossPoint(vector<Point5D> Formula, vector<double> Value) {
for (int i = 0; i < 5; i++) {
int pivot = -1;
for (int j = i; j < 5; j++) {
if (abs(Formula[j].x[i]) > 1e-9) { pivot = j; break; }
}
if (pivot == -1) return Point5D{ -1e9, -1e9, -1e9, -1e9, -1e9 };
swap(Formula[i], Formula[pivot]);
swap(Value[i], Value[pivot]);
for (int j = 0; j < 5; j++) {
if (j == i) continue;
double weight = Formula[j].x[i] / Formula[i].x[i];
for (int k = 0; k < 5; k++) Formula[j].x[k] -= Formula[i].x[k] * weight;
Value[j] -= Value[i] * weight;
}
}
// Return
Point5D ret;
for (int i = 0; i < 5; i++) ret.x[i] = Value[i] / Formula[i].x[i];
return ret;
}
int main() {
// Enumerate 121 Hyperplanes
int pow3[5] = { 1, 3, 9, 27, 81 };
vector<Point5D> List;
for (int i = 122; i < 243; i++) {
Point5D X;
for (int j = 0; j < 5; j++) X.x[j] = ((i / pow3[j]) % 3) - 1;
List.push_back(X);
}
// Enumerate 8495410 Points
vector<Point5D> Candidates;
for (int i = 0; i < 121; i++) {
for (int j = i + 1; j < 121; j++) {
for (int k = j + 1; k < 121; k++) {
for (int l = k + 1; l < 121; l++) {
vector<Point5D> Formula = { List[i], List[j], List[k], List[l] };
vector<double> Value = { 0.0, 0.0, 0.0, 0.0 };
Formula.push_back(Point5D{ 1.0, 0.0, 0.0, 0.0, 0.0 });
Value.push_back(1.0);
Point5D CrossPoint = GetCrossPoint(Formula, Value);
if (CrossPoint.x[0] == -1e9) continue;
if (CrossPoint.x[0] > CrossPoint.x[1] + 1.0e-9) continue;
if (CrossPoint.x[1] > CrossPoint.x[2] + 1.0e-9) continue;
if (CrossPoint.x[2] > CrossPoint.x[3] + 1.0e-9) continue;
if (CrossPoint.x[3] > CrossPoint.x[4] + 1.0e-9) continue;
Candidates.push_back(CrossPoint);
}
}
}
}
// Get Unique Candidates
sort(Candidates.begin(), Candidates.end());
Candidates.erase(unique(Candidates.begin(), Candidates.end()), Candidates.end());
cout << "Number of Candidates = " << Candidates.size() << endl;
return 0;
}
Sample Implementation (C++)
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> Candidates = {
vector<int>{1, 1, 1, 1, 1}, vector<int>{1, 1, 1, 1, 2}, vector<int>{1, 1, 1, 1, 3},
vector<int>{1, 1, 1, 1, 4}, vector<int>{1, 1, 1, 2, 2}, vector<int>{1, 1, 1, 2, 3},
vector<int>{1, 1, 1, 2, 4}, vector<int>{1, 1, 1, 2, 5}, vector<int>{1, 1, 1, 3, 3},
vector<int>{1, 1, 1, 3, 4}, vector<int>{1, 1, 1, 3, 5}, vector<int>{1, 1, 1, 3, 6},
vector<int>{1, 1, 2, 2, 2}, vector<int>{1, 1, 2, 2, 3}, vector<int>{1, 1, 2, 2, 4},
vector<int>{1, 1, 2, 2, 5}, vector<int>{1, 1, 2, 2, 6}, vector<int>{1, 1, 2, 3, 3},
vector<int>{1, 1, 2, 3, 4}, vector<int>{1, 1, 2, 3, 5}, vector<int>{1, 1, 2, 3, 6},
vector<int>{1, 1, 2, 3, 7}, vector<int>{1, 1, 2, 4, 4}, vector<int>{1, 1, 2, 4, 5},
vector<int>{1, 1, 2, 4, 6}, vector<int>{1, 1, 2, 4, 7}, vector<int>{1, 1, 2, 4, 8},
vector<int>{1, 1, 3, 3, 4}, vector<int>{1, 1, 3, 3, 5}, vector<int>{1, 1, 3, 4, 5},
vector<int>{1, 1, 3, 4, 6}, vector<int>{1, 1, 3, 5, 6}, vector<int>{1, 1, 3, 5, 7},
vector<int>{1, 1, 4, 4, 6}, vector<int>{1, 1, 4, 5, 7}, vector<int>{1, 1, 4, 6, 8},
vector<int>{1, 2, 2, 2, 3}, vector<int>{1, 2, 2, 2, 5}, vector<int>{1, 2, 2, 3, 3},
vector<int>{1, 2, 2, 3, 4}, vector<int>{1, 2, 2, 3, 5}, vector<int>{1, 2, 2, 3, 6},
vector<int>{1, 2, 2, 3, 7}, vector<int>{1, 2, 2, 3, 8}, vector<int>{1, 2, 2, 4, 5},
vector<int>{1, 2, 2, 4, 7}, vector<int>{1, 2, 2, 5, 6}, vector<int>{1, 2, 2, 5, 8},
vector<int>{1, 2, 3, 3, 4}, vector<int>{1, 2, 3, 3, 5}, vector<int>{1, 2, 3, 3, 7},
vector<int>{1, 2, 3, 4, 4}, vector<int>{1, 2, 3, 4, 5}, vector<int>{1, 2, 3, 4, 6},
vector<int>{1, 2, 3, 4, 7}, vector<int>{1, 2, 3, 4, 8}, vector<int>{1, 2, 3, 4, 9},
vector<int>{1, 2, 3, 4,10}, vector<int>{1, 2, 3, 5, 6}, vector<int>{1, 2, 3, 5, 7},
vector<int>{1, 2, 3, 5, 9}, vector<int>{1, 2, 3, 6, 7}, vector<int>{1, 2, 3, 6, 8},
vector<int>{1, 2, 3, 6,10}, vector<int>{1, 2, 4, 4, 5}, vector<int>{1, 2, 4, 4, 7},
vector<int>{1, 2, 4, 5, 6}, vector<int>{1, 2, 4, 5, 7}, vector<int>{1, 2, 4, 5, 8},
vector<int>{1, 2, 4, 6, 7}, vector<int>{1, 2, 4, 6, 9}, vector<int>{1, 2, 4, 7, 8},
vector<int>{1, 2, 4, 7,10}, vector<int>{1, 2, 5, 6, 8}, vector<int>{1, 2, 5, 6, 9},
vector<int>{1, 2, 6, 7,10}, vector<int>{1, 3, 3, 4, 5}, vector<int>{1, 3, 3, 5, 7},
vector<int>{1, 3, 4, 4, 6}, vector<int>{1, 3, 4, 5, 6}, vector<int>{1, 3, 4, 5, 7},
vector<int>{1, 3, 4, 6, 8}, vector<int>{1, 3, 4, 7, 9}, vector<int>{1, 3, 4, 8,10},
vector<int>{1, 3, 5, 6, 7}, vector<int>{1, 3, 5, 7, 9}, vector<int>{1, 3, 6, 8,10},
vector<int>{1, 4, 5, 6, 8}, vector<int>{2, 2, 2, 3, 3}, vector<int>{2, 2, 3, 3, 4},
vector<int>{2, 2, 3, 4, 5}, vector<int>{2, 2, 3, 5, 6}, vector<int>{2, 2, 3, 6, 7},
vector<int>{2, 2, 3, 7, 8}, vector<int>{2, 3, 3, 4, 4}, vector<int>{2, 3, 3, 4, 5},
vector<int>{2, 3, 3, 4, 8}, vector<int>{2, 3, 4, 4, 5}, vector<int>{2, 3, 4, 5, 6},
vector<int>{2, 3, 4, 5, 8}, vector<int>{2, 3, 4, 6, 7}, vector<int>{2, 3, 4, 7, 8},
vector<int>{2, 3, 4, 8, 9}, vector<int>{2, 3, 4, 9,10}, vector<int>{2, 3, 5, 6, 7},
vector<int>{2, 3, 6, 7, 8}, vector<int>{2, 4, 5, 6, 7}, vector<int>{2, 4, 5, 7, 8},
vector<int>{2, 5, 6, 8, 9}, vector<int>{3, 4, 4, 5, 6}, vector<int>{3, 4, 5, 6, 7},
vector<int>{3, 4, 5, 6, 8}, vector<int>{4, 5, 6, 7, 8}
};
long long GetError(int N, vector<vector<int>> &A, vector<int> &R, vector<int> Score) {
vector<pair<int, int>> Sorted;
// Determine Order
for (int i = 0; i < N; i++) {
int sum = 0;
for (int j = 0; j < 5; j++) sum += A[i][j] * Score[j];
Sorted.push_back(make_pair(sum, -R[i]));
}
sort(Sorted.begin(), Sorted.end());
reverse(Sorted.begin(), Sorted.end());
// Calculate Error
long long Error = 0;
for (int i = 0; i < N; i++) {
int idx1 = -Sorted[i].second;
int idx2 = i + 1;
Error += 1LL * (idx1 - idx2) * (idx1 - idx2);
}
return Error;
}
int main() {
int T; cin >> T;
for (int t = 1; t <= T; t++) {
// Input
int N; cin >> N;
vector<vector<int>> A(N, vector<int>(5, 0));
vector<int> R(N, 0);
for (int i = 0; i < N; i++) {
for (int j = 0; j < 5; j++) cin >> A[i][j];
}
for (int i = 0; i < N; i++) cin >> R[i];
// Solve
long long Answer = (1LL << 60);
for (vector<int> cand : Candidates) {
long long ret = GetError(N, A, R, cand);
Answer = min(Answer, ret);
}
cout << Answer << endl;
}
return 0;
}
posted:
last update: