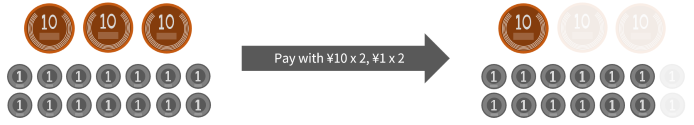We hope you enjoyed this contest. Although there were many difficult problems, we hope you found them enjoyable.

For beginners

• If you have just started programming and are unsure where to begin, try problem A "Welcome to AtCoder" in the practice contest first.
• If you are not familiar with programming contests, we recommend trying some problems from the AtCoder Beginners Selection.
• [Translator's Note: If the above applies to you, you can ignore AtCoder Regular Contest for a while and focus on AtCoder Beginner Contest.]

---

Case with only 1-yen and 10-yen coins

This problem is complicated due to the presence of six types of coins, so let’s first consider the following problem limited to just \(1\)-yen and \(10\)-yen coins.

Problem Mr. AtCoder has \(A\) 1-yen coins and \(C\) 10-yen coins. He will shop at \(N\) stores in sequence, spending \(X_1, \dots, X_N\) yen. Determine if it is possible to pay the exact amount at each store.

1. Consider a concrete example

For example, consider having fourteen \(1\)-yen coins and three \(10\)-yen coins, and planning to spend \(22\) yen at the first store and \(13\) yen at the second store. Let’s start with the \(22\) yen purchase.

One possible way to pay is “two \(10\)-yen coins and two \(1\)-yen coins”.

Another possible way to pay is “one \(10\)-yen coin and twelve \(1\)-yen coins”.

Next, we need to make a \(13\) yen purchase. In the first case, it is possible to pay exactly with one \(10\)-yen coin and three \(1\)-yen coins. However, in the second case, it is not possible to pay the exact amount.

Why did the first case succeed while the second case failed?

2. Use 10-yen coins when you can

The reason why we couldn’t pay exactly \(13\) yen in the second case is that we needed at least three \(1\)-yen coins but only had two left. This was because we used up twelve \(1\)-yen coins in the first purchase, leaving us short. Conversely, the first case was successful because we conserved our \(1\)-yen coins.

There is absolutely no benefit to using an additional ten \(1\)-yen coins for a purchase when you have \(10\)-yen coins left. This is because, if you use the \(10\)-yen coin for a future purchase, it’s essentially the same as using that \(10\)-yen coin for the current purchase and then using ten \(1\)-yen coins for that future purchase.

Therefore, the optimal strategy is to use as many \(10\)-yen coins as possible and save as many \(1\)-yen coins as possible. By simulating this strategy, if you can pay at all stores, the answer is Yes; otherwise, the answer is No.

---

Solution to the original problem

The same logic applies even when there are \(1\), \(5\), \(10\), \(50\), \(100\), and \(500\)-yen coins. There is no benefit in saving higher-value coins to pay with lower-value coins for each purchase.

Formal proof (advanced)

Claim: Let $(p_1, p_2, \dots, p_6) = (1, 5, 10, 50, 100, 500)$. It is impossible to be in a situation where "for the purpose of achieving the goal, it is absolutely necessary to pay with $p_1, \dots, p_{i-1}$ yen coins amounting to at least $p_i$ yen while keeping $p_i$ yen coins" at the time of a certain purchase X.

Let's say we used $a_1, \dots, a_{i-1}$ coins of $p_1, \dots, p_{i-1}$ yen respectively $(a_1 p_1 + \dots + a_{i-1} p_{i-1} \geq p_i)$ for purchase X. First, we prove that it's possible to select some of these coins to exactly make $p_i$ yen. Consider the largest $k$ such that $a_k p_k \dots + a_{i-1} p_{i-1} \geq p_i$. Let $s = a_{k+1} p_{k+1} \dots + a_{i-1} p_{i-1}$. Then, by using $\frac{p_i-s}{p_k}$ coins of $p_k$ yen and $a_{k+1}, \dots, a_{i-1}$ coins of $p_{k+1}, \dots, p_{i-1}$ yen respectively, we can exactly make $p_i$ yen. Here, $\frac{p_i-s}{p_k}$ must be an integer because both $s$ and $p_i$ are multiples of $p_k$.

With the aforementioned selection of coins denoted as $S$, the claim can be demonstrated as follows:

• If we don't use any $p_i$ yen coins for future purchases: For purchase X, we can use a $p_i$ yen coin instead of the coins in $S$.
• If we use $p_i$ yen coins for future purchases: For purchase X, we can use a $p_i$ yen coin instead of the coins in $S$, and for future purchases, we can use $S$ instead of a $p_i$ yen coin.

Therefore, the optimal strategy for each purchase is as follows.

• Pay with \(500\)-yen coins as much as possible until the remaining amount is less than \(499\) yen or you run out of \(500\)-yen coins
• (Omitted)
• Pay with \(5\)-yen coins as much as possible until the remaining amount is less than \(5\) yen or you run out of \(5\)-yen coins
• Pay the remaining amount with \(1\)-yen coins

By simulating this strategy, if you can pay at all stores, the answer is Yes; otherwise, the answer is No.

---

Sample Implementation

A sample implementation in C++ is at https://atcoder.jp/contests/arc177/submissions/53283608.

In Python, the solution can be implemented as follows:

# Input
a, b, c, d, e, f = map(int, input().split())
n = int(input())
x = list(map(int, input().split()))

# Simulation
ans = True
for v in x:
	while v >= 500 and f >= 1:
		v -= 500
		f -= 1
	while v >= 100 and e >= 1:
		v -= 100
		e -= 1
	while v >= 50 and d >= 1:
		v -= 50
		d -= 1
	while v >= 10 and c >= 1:
		v -= 10
		c -= 1
	while v >= 5 and b >= 1:
		v -= 5
		b -= 1
	while v >= 1 and a >= 1:
		v -= 1
		a -= 1
	if v != 0:
		ans = False
		break

# Output
print('Yes' if ans == True else 'No')