ステップ 1

まず、どのような移動戦略が最適であるかについて考察してみましょう。

A 社の優待券を持っている住民を西から順に青 \(1\)、青 \(2\)、青 \(3\)…、と呼ぶことにします。また、J 社の優待券を持っている住民を西から順に赤 \(1\)、赤 \(2\)、赤 \(3\)…、と呼ぶことにします。このとき、赤 \(2\) の住民が荷物にふれた後に赤 \(1\) の住民が荷物にふれるなど、同じ色の中で順番が逆転するような移動方法は最適ではありません。なぜなら、下図のように赤 \(1\) と赤 \(2\) の順序を入れ替えた方がコストが小さくなるからです。

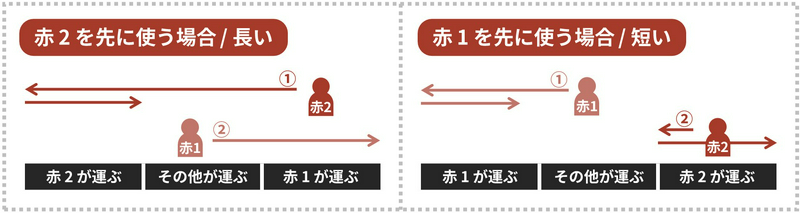
この性質を使うと、以下の \(4\) つの状態を持ち、現在の最小コストを記録した動的計画法が自然に思いつきます。

• 現在の位置 \(\mathrm{pos}\)
• 現在青の何番まで使ったか \(b\)
• 現在赤の何番まで使ったか \(r\)
• 現在青と赤のどちらが荷物を持っているか \(\mathrm{type}\)

つまり \(\mathrm{dp}[\mathrm{pos}][b][r][\mathrm{type}] = (最小コスト)\) という形の動的計画法です。しかし、この動的計画法の状態数は \(O(N^3)\) であるため、残念ながら本問題の制約では大差で TLE となってしまいます。

---

ステップ 2

それでは、状態数をもっと削ることはできないのでしょうか。

まず、現在位置の \(2\) 個以上左の青、\(2\) 個以上左の赤の住民は荷物をさわらないと考えてかまいません。厳密には、位置 \(\mathrm{pos}\) より左にいる青・赤の住民の人数をそれぞれ \(b_{\mathrm{left}}, r_{\mathrm{left}}\) 人とするとき、\(\mathrm{dp}[\mathrm{pos}][b][r][\mathrm{type}]\) において \(b \geq b_{\mathrm{left}}, r \geq r_{\mathrm{left}}\) を仮定しても問題ありません。

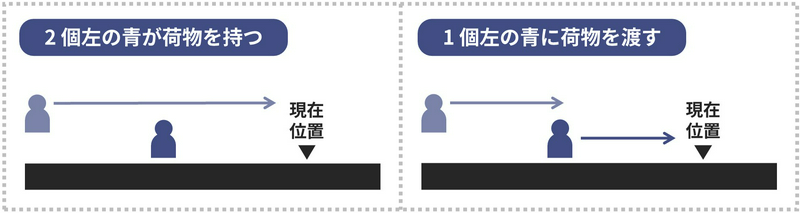
なぜなら、下図左のように「\(2\) 個左の青の住民」に荷物をさわらせるのと、下図右のように「\(1\) 個左の青の住民」のいる場所に到達したタイミングでその人に荷物を渡すのではコストが変わらないからです。

しかし、この改善をしてもまだ状態数は \(O(N^3)\) で変わらないため、TLE になってしまいます。

---

ステップ 3

それでは、状態数をさらに削ることはできないのでしょうか。

ステップ 2 では現在位置を左から抑えましたが、実は右から抑えることも可能です。具体的には、本問題の制約下では現在位置の \(20\) 個以上右の青、\(20\) 個以上右の赤の住民は荷物をさわらないと考えて構いません。厳密に書き下すと、位置 \(\mathrm{pos}\) より左にいる青・赤の住民の人数をそれぞれ \(b_{\mathrm{left}}, r_{\mathrm{left}}\) とするとき、\(\mathrm{dp}[\mathrm{pos}][b][r][\mathrm{type}]\) において \(b \leq b_{\mathrm{left}} + 20, r \leq r_{\mathrm{left}} + 20\) を仮定しても問題ありません。

---

これは一体なぜなのでしょうか。上限の \(20\) で抑えられなさそうな最悪ケースとして、以下のケースを考えてみましょう。

• 青の住民：位置 \(L-1\) 以左には存在せず、位置 \(L\) に \(21\) 人存在する
• 赤の住民：あらゆるところに存在する

このケースでは、もし右図のように \(21\) 回の青の住民へのバトンパスが起これば、上限を \(20\) で抑えられないことになります。なお、これが最悪ケースになっている理由は、直感的には「赤の住民が減るほど \(1\) 人の青が長い距離を担当しやすくなること」および「青の住民が位置 \(L-1\) 以左にいるより位置 \(L\) にいる方がゴール地点での \(b - b_{\mathrm{left}}\) の値を稼ぎやすくなること」から説明できます。

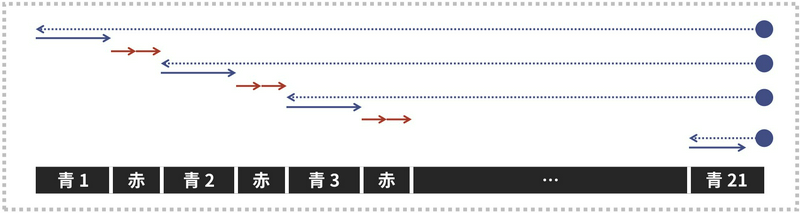
そこで、\(L \leq 6 \times 10^4\) の制約下でこのようなことが起こるかを考えます。

青 \(1\)、青 \(2\)、青 \(3\)…、青 \(20\) と書かれた場所の右にある「赤が運ぶ部分」に含まれる赤 (J 社) の飛行機の数を順に \(r_1, r_2, \dots, r_{20}\) とします。このとき、まず (1) のコストが (2) のコストより小さくなければならないので、\(r_1 \geq r_2 + r_3 + \dots + r_{20}\) を満たします。

1. 下図左のように、青 \(1\) の住民が「青 \(1\)」と書かれたところだけで運ぶ
2. 下図右のように、青 \(1\) の住民が「青 \(2\)」と書かれたところまでを運ぶ

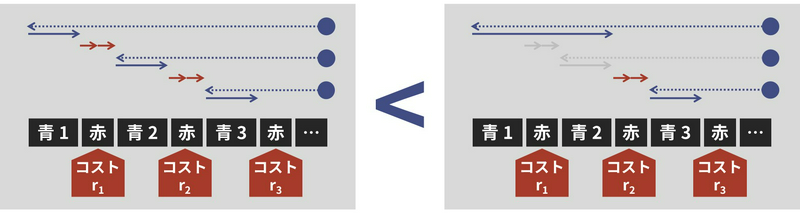
また、下の (1) のコストが (2) より小さくなければならないので、\(r_2 \geq r_3 + r_4 + \dots + r_{20}\) を満たします。

1. 青 \(2\) の住民が「青 \(3\)」と書かれたところだけで運ぶ
2. 青 \(2\) の住民が「青 \(4\)」と書かれたところまでを運ぶ

さらに、下の (1) のコストが (2) より小さくなければならないので、\(r_3 \geq r_4 + r_5 + \dots + r_{20}\) を満たします。\(r_4, r_5, \dots\) についても同様です。

1. 青 \(3\) の住民が「青 \(4\)」と書かれたところだけで運ぶ
2. 青 \(3\) の住民が「青 \(5\)」と書かれたところまでを運ぶ

そして、もし \(r_{20} = 0\) の場合、青 \(20\) の住民が最後まで運ぶのが最適になり \(21\) 人目が不要となってしまうため、\(r_{20} \geq 1\) です。したがって、\(r_{19} \geq 1, r_{18} \geq 2, r_{17} \geq 4, \dots, r_1 \geq 2^{18}\) となり、\(L \leq 6 \times 10^4\) の制約と矛盾します。

以上より、右に関しても \(20\) 個先までで抑えられることが証明できました。

---

実装例 (C++)

以下、C++ での実装例を示します。実装における注意点としては、以下が挙げられます。

• 同じ位置に複数の住民がいる場合の処理に注意する
• メモリの管理方法を工夫せずに \(O(N^3)\) 状態持つと ML E することに注意する
• \(K = 20\) として遷移に \(O(K)\) かけると TLE することに注意する

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct agent {
	int x; char c;
};

// col 社の優待券を持っている人が地点 start から goal まで移動するのに何コイン必要かを返す関数
int GetCost(int start, int goal, char col, vector<int>& SumA, vector<int>& SumJ) {
	if (start > goal) swap(start, goal);
	if (col == 'A') return SumJ[goal] - SumJ[start];
	if (col == 'J') return SumA[goal] - SumA[start];
	return -1;
}

int Solve(int L, int N, const string& S, const vector<agent>& A) {
	vector<vector<vector<vector<int>>>> dp(L + 5, vector<vector<vector<int>>>(22, vector<vector<int>>(22, vector<int>(3, (1 << 29)))));
	vector<int> CountA(L + 5, 0);
	vector<int> CountJ(L + 5, 0);
	vector<int> SumA(L + 5, 0);
	vector<int> SumJ(L + 5, 0);
	vector<int> ListA;
	vector<int> ListJ;

	// Step 1. 各地点 i について、地点 i より左に何人の A, J の優待券を持っている人がいるかを計算
	// それぞれ CountA, CountJ に記録
	// また、人の座標のリストをそれぞれ ListA, ListJ に記録
	for (int i = 0; i < N; i++) {
		if (A[i].c == 'A') { CountA[A[i].x + 1] += 1; ListA.push_back(A[i].x); }
		if (A[i].c == 'J') { CountJ[A[i].x + 1] += 1; ListJ.push_back(A[i].x); }
	}
	ListA.push_back(L + 1);
	ListJ.push_back(L + 1);
	for (int i = 0; i <= L + 2; i++) CountA[i + 1] += CountA[i];
	for (int i = 0; i <= L + 2; i++) CountJ[i + 1] += CountJ[i];
	sort(ListA.begin(), ListA.end());
	sort(ListJ.begin(), ListJ.end());

	// Step 2. 各地点 i について、地点 i より左に何個の A, J の飛行機があるかを計算
	// それぞれ配列 SumA, SumJ に記録
	for (int i = 0; i < L; i++) {
		if (S[i] == 'A') SumA[i + 1] += 1;
		if (S[i] == 'J') SumJ[i + 1] += 1;
	}
	for (int i = 0; i <= L; i++) SumA[i + 1] += SumA[i];
	for (int i = 0; i <= L; i++) SumJ[i + 1] += SumJ[i];
	SumA[L + 1] = (1 << 28);
	SumJ[L + 1] = (1 << 28);

	// Step 3. 動的計画法の初期化
	for (int i = 0; i <= L; i++) {
		for (int j = 0; j < 20; j++) {
			for (int k = 0; k < 20; k++) dp[i][j][k][0] = (1 << 29);
			for (int k = 0; k < 20; k++) dp[i][j][k][1] = (1 << 29);
			for (int k = 0; k < 20; k++) dp[i][j][k][2] = (1 << 29);
		}
	}
	dp[0][2][2][0] = 0;

	// Step 4. 動的計画法 (実際の計算)
	for (int i = 0; i < L; i++) {
		for (int j = 0; j < 20; j++) {
			for (int k = 0; k < 20; k++) {
				int IndexA = (j - 2) + CountA[i]; if (IndexA < 0 || IndexA >= ListA.size()) continue;
				int IndexJ = (k - 2) + CountJ[i]; if (IndexJ < 0 || IndexJ >= ListJ.size()) continue;

				// 遷移先を計算
				int posA = max(0, IndexA - CountA[i + 1] + 2);
				int posJ = max(0, IndexJ - CountJ[i + 1] + 2);

				// コストを計算
				int cstA = GetCost(ListA[IndexA], i, 'A', SumA, SumJ);
				int cstJ = GetCost(ListJ[IndexJ], i, 'J', SumA, SumJ);

				// 0 -> * の遷移
				if (posA >= 1) dp[i + 1][posA][posJ][1] = min(dp[i + 1][posA][posJ][1], dp[i][j][k][0] + cstA + (S[i] == 'A' ? 0 : 1));
				if (posJ >= 1) dp[i + 1][posA][posJ][2] = min(dp[i + 1][posA][posJ][2], dp[i][j][k][0] + cstJ + (S[i] == 'J' ? 0 : 1));

				// * -> 0 の遷移
				if (j + 1 < 20) dp[i][j + 1][k][0] = min(dp[i][j + 1][k][0], dp[i][j][k][1]);
				if (j + 1 < 20) dp[i][j + 1][k][0] = min(dp[i][j + 1][k][0], dp[i][j][k][0]);
				if (k + 1 < 20) dp[i][j][k + 1][0] = min(dp[i][j][k + 1][0], dp[i][j][k][2]);
				if (k + 1 < 20) dp[i][j][k + 1][0] = min(dp[i][j][k + 1][0], dp[i][j][k][0]);

				// * -> * の遷移
				dp[i + 1][posA][posJ][1] = min(dp[i + 1][posA][posJ][1], dp[i][j][k][1] + (S[i] == 'A' ? 0 : 1));
				dp[i + 1][posA][posJ][2] = min(dp[i + 1][posA][posJ][2], dp[i][j][k][2] + (S[i] == 'J' ? 0 : 1));
			}
		}
	}

	// Step 5. 答えを求める
	int Answer = (1 << 29);
	for (int i = 0; i < 20; i++) {
		for (int j = 0; j < 20; j++) {
			for (int k = 0; k < 3; k++) Answer = min(Answer, dp[L][i][j][k]);
		}
	}
	return Answer;
}

int main() {
	// 入力
	int L, N; string S;
	cin >> L >> N;
	cin >> S;
	vector<agent> A(N);
	for (int i = 0; i < N; i++) cin >> A[i].x >> A[i].c;

	// 出力
	cout << Solve(L, N, S, A) << endl;
	return 0;
}