How was this contest for you? Compared to an average ARC, we think it was a considerably challenging set of problems, but we hope you enjoyed it. Now, let’s start the explanation.

For beginners

• If you have just started programming and are unsure where to start, try problem A “Welcome to AtCoder” in the practice contest.
• Also, if you are not familiar with programming contests, we recommend trying some problems from the AtCoder Beginners Selection.

For novices (with AtCoder Rating below 400)

• This time the problems were particularly difficult, but generally, the problems in AtCoder Regular Contest (ARC) are significantly harder than those in AtCoder Beginner Contest (ABC).
• If you found ARC too difficult, we recommend participating in ABC or solving past ABC problems.
• For practicing past problems, websites like AtCoder Problems are very useful, so I recommend using them.

---

Step 1

First, let’s consider the following three specific examples for a chocolate bar of size \(7 \times 11\).

• Can you give \(28\) pieces of \(1 \times 1\), \(5\) pieces of \(2 \times 2\), and \(2\) pieces of \(4 \times 4\)?
• Can you give \(10\) pieces of \(1 \times 1\), \(8\) pieces of \(2 \times 2\), and \(2\) pieces of \(4 \times 4\)?
• Can you give \(10\) pieces of \(1 \times 1\), \(1\) piece of \(2 \times 2\), and \(3\) pieces of \(4 \times 4\)?

Answer for example 1

In this example, it is impossible to give chocolate to everyone. This is because the total area of the chocolate bars to be given exceeds \(80\), which is more than the area of the chocolate bar you have, \(7 \times 11 = 77\).

Answer for example 2

In this example, again, it is impossible to give chocolate to everyone. This is because the total area of the chocolate bars of size \(2 \times 2\) or larger to be given exceeds \(64\), which is more than \(60\). Here, we explain why it’s impossible if the area exceeds \(60\).

• First, note that you can give at most \(15\) pieces of \(2 \times 2\) chocolate bars as shown in the figure below.
• Therefore, you cannot give chocolate bars of size \(2 \times 2\) or larger with a total area exceeding \(60\).
• Moreover, giving chocolate bars of size \(2 \times 2\) or larger with a total area of \(x\) is harder than giving \(2 \times 2\) chocolate bars with a total area of \(x\).
• Therefore, you cannot give chocolate bars of size \(2 \times 2\) or larger with a total area exceeding \(60\).

The proof that you can only give \(15\) pieces of \(2 \times 2\) chocolate bars is described at the end of the explanation. For now, please intuitively accept it as correct.

Answer for example 3

In this example, again, it is impossible to give chocolate to everyone. This is because you can only give two pieces of \(4 \times 4\) chocolate bars as shown in the figure below.

Step 2

So far, from the specific examples, we have identified the following three conditions for the answer to be No. (The third condition is converted into an area form for easier processing later)

• The total area of chocolate bars of size \(1 \times 1\) or larger exceeds \(77\)
• The total area of chocolate bars of size \(2 \times 2\) or larger exceeds \(60\)
• The total area of chocolate bars of size \(4 \times 4\) or larger exceeds \(32\)

Now, if all three conditions are unmet, does it mean the answer is Yes? It does. The reason can be explained as follows.

View explanation

By following the steps below to give out chocolate bars, you can always give out all the chocolate bars.

• Take out the required number of \(4 \times 4\) chocolate bars from the top left, fitting within the \(4 \times 8\) area, in order from the top left.
• Take out the required number of \(2 \times 2\) chocolate bars from the top left, fitting within the \(6 \times 10\) area, in order from the top left.
• Take out the required number of \(1 \times 1\) chocolate bars from the top left, fitting within the \(7 \times 11\) area, in order from the top left.

For example, if you need to give \(20\) pieces of \(1 \times 1\), \(10\) pieces of \(2 \times 2\), and \(1\) piece of \(4 \times 4\), the procedure would be as shown in the figure below.

Step 3

Finally, let’s generalize the considerations so far to cases where the size of the chocolate bar is not \(7 \times 11\). First, if the following conditions are met, the answer is No. (\(\lfloor x \rfloor\) denotes \(x\) rounded down to an integer.)

• The total area of chocolate bars of size \(1 \times 1\) or larger exceeds \(H \times W\)
• The total area of chocolate bars of size \(2 \times 2\) or larger exceeds \(\lfloor H/2 \rfloor \times \lfloor W/2 \rfloor \times 2^2\)
• The total area of chocolate bars of size \(4 \times 4\) or larger exceeds \(\lfloor H/4 \rfloor \times \lfloor W/4 \rfloor \times 4^2\)
• The total area of chocolate bars of size \(8 \times 8\) or larger exceeds \(\lfloor H/8 \rfloor \times \lfloor W/8 \rfloor \times 8^2\)
• Similarly for \(16 \times 16\), \(32 \times 32\), etc.

Also, similar to Step 2, if all the above conditions are unmet, the answer is yes. Therefore, implementing a program to calculate the total areas, as shown in the following sample implementations, will get you AC.

Note that under the constraints of this problem, the total area can be around \(10^{18}\), so using a \(32\)-bit integer type like int may cause overflow. Use a \(64\)-bit integer type like long long to get the correct answer.

---

Sample Implementation (C++)

#include <iostream>
using namespace std;

long long H;
long long W;
long long N;
long long A[1009];

// Function to return the total area of chocolate bars to be given of size (2^r) * (2^r) or larger
long long TotalArea(long long r) {
	long long Area = 0;
	for (int i = 1; i <= N; i++) {
		if (A[i] >= r) {
			// Note that 2 to the power of A[i] can be calculated as (1LL << A[i])
			Area += (1LL << A[i]) * (1LL << A[i]);
		}
	}
	return Area;
}

// Main function
int main() {
	// Step 1. Input
	cin >> H >> W >> N;
	for (int i = 1; i <= N; i++) {
		cin >> A[i];
	}

	// Step 2. Check the conditions for sizes 1, 2, 4, ..., (2^25)
	// Note that 2^r can be calculated as (1LL << r)
	for (int r = 0; r <= 25; r++) {
		long long LimitH = (H / (1LL << r)); // Rounding down (H / (2^r))
		long long LimitW = (W / (1LL << r)); // Rounding down (W / (2^r))
		long long LimitArea = LimitH * LimitW * (1LL << r) * (1LL << r); // Area limit

		// Compare with the total area to be given
		long long ActualArea = TotalArea(r);

		// If it exceeds the limit, the answer is immediately No
		if (ActualArea > LimitArea) {
			cout << "No" << endl;
			return 0;
		}
	}

	// Step 3. If all conditions are met, output Yes
	cout << "Yes" << endl;
	return 0;
}

Sample Implementation (Python)

import sys

# Function to return the total area of chocolate bars to be given of size (2^r) * (2^r) or larger
def TotalArea(H, W, N, A, r):
    Area = 0
    for i in A:
        if i >= r:
            Area += (2 ** i) * (2 ** i)
    return Area

# Step 1. Input
H, W, N = map(int, input().split())
A = list(map(int, input().split()))

# Step 2. Check the conditions for sizes 1, 2, 4, ..., (2^25)
for r in range(0, 26):
    LimitH = H // (2 ** r) # Rounding down H / (2^r)
    LimitW = W // (2 ** r) # Rounding down W / (2^r)
    LimitArea = LimitH * LimitW * (2 ** r) * (2 ** r) # Area limit

    # Compare with the total area to be given
    ActualArea = TotalArea(H, W, N, A, r)

    # If it exceeds the limit, the answer is immediately No
    if ActualArea > LimitArea:
        print("No")
        sys.exit(0)

# Step 3. If all conditions are met, output Yes
print("Yes")

---

Supplement: Proof for Step 1

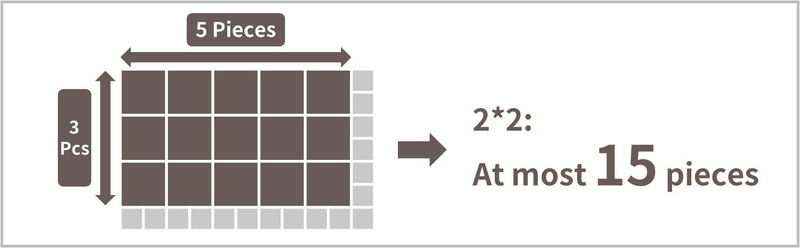
In the explanation for Step 1, we mentioned that when you have a \(7 \times 11\) chocolate bar, you can only take out \(15\) pieces of \(2 \times 2\) chocolate bars, which we described as “intuitively correct”. But how can this be proven?

• First, consider painting the squares at every second row from the top and every second column from the left in red, as shown in the figure below.
• In this case, there are a total of \(3 \times 5 = 15\) red squares.
• However, a \(2 \times 2\) chocolate bar must always contain one red square, so you can take out at most \(15\) pieces.

Similarly, it can also be proven that you can only take out at most \(\lfloor H/L \rfloor \times \lfloor W/L \rfloor\) pieces of \(L \times L\) chocolate bars from an \(H \times W\) chocolate bar.