E - BDFS 解説
by  potato167
potato167
解説を元にした高速化
行列累乗や線形漸化式の形で表せることは他の解説に示されている通りですが、より閉じた形で答えを表すことが可能です。
その方法と式、そしてメリットについて記します。
問題に対する考察は基本的にスキップします。
[1] 行列累乗による答えの表現
まず、 \(p=\frac{P}{100}\) とします。
https://twitter.com/NachiaVivias/status/1749481600751132968
このツイートを参考にして行列を構築します。
答え : \(\text{ans}\)
キューの先頭のノードの距離 : \(\text{D}\)
ターン数 : \(\text{turn}\)
とすると、\(1\) ターンでの変数の遷移は以下のようになります。
- \(\text{ans}\leftarrow \text{D}\)
- \(\text{D}\leftarrow (\text{D}+1)p+(\text{turn}-\text{D})(1-p)\)
- \(\text{turn}\leftarrow\text{turn}+1\)
この遷移を \((\text{ans},\text{D},\text{turn},\text{const})\) に対する行列で表すと以下のようになります。
\[ \left( \begin{matrix} 1 & 0 & 0 & 0\\ 1 & 2p-1 & 0 & 0\\ 0 & 1-p & 1 & 0\\ 0 & p & 1 & 1 \end{matrix} \right) \]
この行列を \((\text{ans},\text{D},\text{turn},\text{const})=(0,1,2,1)\) で初期化した状態の行列に \(N-1\) 回かけて最後に \(\text{ans}\) に入っている値が答えです。
[2] 形式的冪級数を用いた寄与の表現
この行列遷移をグラフで表すと以下のようになります。
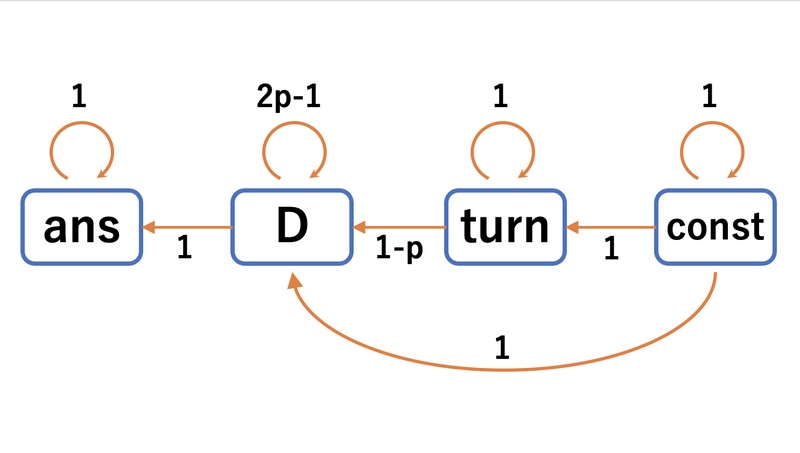
これを見て、\(\text{ans}\) に対する寄与を形式的冪級数を用いて考えます。
つまり、\([x^a]f(x)\) が \(a\) ターン目の \(\text{ans}\) となるような \(f(x)\) がどのように表されるかを考えます。
- \(\text{D}\) の寄与
\(\dfrac{x}{1-x}\times \dfrac{1}{1-(2p-1)x}\)
- \(\text{turn}\) の寄与
\(\dfrac{x}{1-x}\times \dfrac{1}{1-(2p-1)x}\times (1-p)x\times\dfrac{1}{1-x}\)
- \(\text{const}\) の寄与
\(\dfrac{x}{1-x}\times \dfrac{1}{1-(2p-1)x}\times (x+(1-p)x\times\dfrac{x}{1-x})\times \dfrac{1}{1-x}\)
\(\text{turn}\) の寄与を \(2\) 倍して、これらの和を取ると以下のようになります。
\[\dfrac{x(1-px)}{(1-x)^{3}(1-(2p-1)x)}\]
上記の式の \(N-1\) 次の係数が求めたい答えです。
[3] 計算
ここから、気合いで計算します。
まず、以下の式が成り立ちます。
\[\dfrac{1}{(1-x)^{3}(1-(2p-1)x)}=\dfrac{1}{(2-2p)(1-x)^{3}}+\dfrac{(1-2p)}{(2-2p)^2(1-x)^2}+\dfrac{(1-2p)^2}{(2-2p)^3(1-x)}+\dfrac{(1-2p)^3}{(2-2p)^3(1-(2p-1)x)}\]
また、一般に以下の式が成り立ちます。
\[[x^{a}]\dfrac{1}{(1-bx)^c}=\text{Bi}(a+c-1,a)b^a\]
これらを用いると、値が簡単に求められます。
この式を用いて式変形をすると、答えを表す式は最終的に以下のような形になります。
\[\dfrac{(2p-1)^{N}-1}{8(p-1)^{2}}-\dfrac{Np}{4(1-p)}+\dfrac{N^{2}}{4}\]
よって、この式の値を求めるコードを書けば AC を得ることができます。
[4] メリット
- 早い実行時間で終わる
計算量は変わらず \(O(T\log(N))\) ですが、行列累乗が定数倍で次数の \(3\) 乗かかるのに対して、こちらの解法は単なる整数の冪乗なので定数倍が軽いです。
よって実行時間が短く、分母の値を前計算しておくことで、投稿時での fastest を取ることができました。
- 短いバイト数で書ける
行列累乗等の複雑な計算をしないため、シンプルにコードを書くことができます。実際に python を用いて投稿時での shortest を取ることができました。
投稿日時:
最終更新: