F - Tri-Colored Paths Editorial by evima
Hints → https://atcoder.jp/contests/arc153/editorial/5482
This editorial assumes basic knowledge of biconnected components and block-cut trees of a graph. Here are some websites on these topics:
Let us call a coloring bad when it satisfies the following.
- Edges in every color exist.
- The condition in question is not satisfied. That is, any simple path contains edges in two or fewer colors.
The problem can be easily reduced to the counting of bad colorings, which we will explain below.
[1] On \(3\)-color cycles
Let us show the following.
In a bad coloring, let \(C\) be a \(3\)-color cycle. Then, the following holds.
- \(C\) has a length of \(3\).
- If \(N\geq 5\), there is exactly one vertex in \(C\) that is adjacent to a vertex outside \(C\).
First, if the length of \(C\) were \(4\) or greater, a simple path formed from \(C\) except one edge would contain all colors, which is a contradiction.
Assume that the length of \(C\) is \(3\). Let \(v_1\), \(v_2\), and \(v_3\) be the vertices in \(C\), and assume that the colors of edges \(v_1v_2\), \(v_2v_3\), and \(v_3v_1\) are \(3\), \(1\), and \(2\), respectively. Let us assume for contradiction that \(N\geq 5\) and both \(v_1\) and \(v_2\) are adjacent to vertices outside \(C\).
Let \(x\) be a vertex outside \(C\) adjacent to \(v_1\), and \(y\) be a vertex outside \(C\) adjacent to \(v_2\).
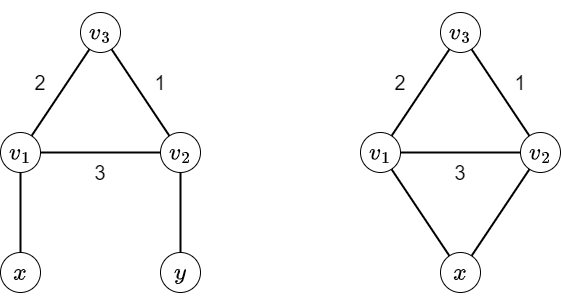
From the simple paths \((x,v_1,v_2,v_3)\) and \((x,v_1,v_3,v_2)\), the color of the edge \(xv_1\) is \(1\). Similarly, the color of the edge \(yv_2\) is \(2\).
Then, if we let \(S = \{v_1,v_2,v_3,x\}\), for any \(s\in S\) and two colors \(a\) and \(b\), there is a simple path in \(S\) starting from \(s\) that contains the colors \(a\) and \(b\). When \(N\geq 5 > |S|\), there is an edge connecting some \(s\in S\) and \(t\notin S\), but combining such an edge and a simple path in \(S\) starting from \(s\) yields a simple path containing all colors, a contradiction.
From the above observations, one can count bad colorings with \(3\)-color cycles. When \(N\leq 4\), the problem can be solved by checking all possible colorings and simple paths, so let us assume \(N\geq 5\) below.
Such a coloring satisfies the following for a cycle \(C = (v_1,v_2,v_3)\) and different colors \(a\), \(b\), and \(c\).
- \(C\) is one of the biconnected components of \(G\), and \(v_1\) is the only cut vertex of \(G\) in \(C\).
- The colors of \(v_1v_2\), \(v_2v_3\), and \(v_3v_1\) are \(c\), \(a\), and \(b\), respectively.
Here, for any edge \(e\) not in \(C\), there is a simple path that contains the edges \(e, v_1v_2, v_2v_3\), so the color of \(e\) is not \(b\). Similarly, that color is not \(c\), so it must be \(a\).
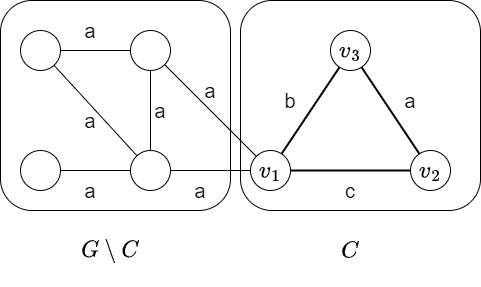
On the other hand, one can easily verify that such a coloring is always bad and contains a single \(3\)-color cycle. Thus, when \(N\geq 5\), one can count bad colorings containing \(3\)-color cycles, as follows.
- Let \(n\) be the number of length-\(3\) cycles \(C\) that is one of the biconnected components of \(G\) and contains a single cut vertex of \(G\).
- Then, there are \(6n\) bad colorings containing \(3\)-color cycles.
[2] On \(2\)-color cycles
Let us show the following.
There is no bad coloring that contains a \(2\)-color cycle but not a \(3\)-color cycle.
Consider a bad coloring, and let \(C\) be a cycle containing colors \(1\) and \(2\) but not \(3\). Then, for any \(x\in C\), there is a simple path starting from \(x\) and composed of edges in \(C\) that contains both colors \(1\) and \(2\).
Let us show that no edge \(e\) has color \(3\).

Assume that \(e\) is an edge outside \(C\). If the color of \(e\) were \(3\), one can take a simple path containing \(e\) and reaching \(C\), and combine it with a simple path in \(C\) to yield a path containing all colors, a contradiction.
Assume that \(e\) is a chord in \(C\) (an edge that is not part of \(C\) but connects two vertices in \(C\)). Also, assume that \(e\) has color \(3\). \(e\) divides the edges in \(C\) into two parts \(C_1\) and \(C_2\). From the assumption that the coloring does not contain a \(3\)-color cycle, the number of colors of edges in \(C_1\) is \(1\). Similarly, the number of colors of edges in \(C_2\) is also \(1\). Then, adding edges from \(C_1\) and \(C_2\) before and after \(e\) yields a \(3\)-color simple path, which contradicts the fact that the coloring is bad.
Therefore, it has been shown that no edge has color \(3\), which violates the definition of bad coloring.
[3] On bad colorings with just \(1\)-color cycles
Let us study bad colorings all of whose cycles are \(1\)-colored. In such a coloring, all edges in each biconnected component of \(G\) have the same color. Thus, the problem can be reduced to the following one on block-cut trees.
Count the number of ways to color each block of the block-cut tree \(T\) of \(G\) in color \(1\), \(2\), or \(3\) so that the following are satisfied.
- There is a block in every color.
- There is no simple path in \(T\) that contains a block in every color.
Let us call such a coloring of \(T\) bad.
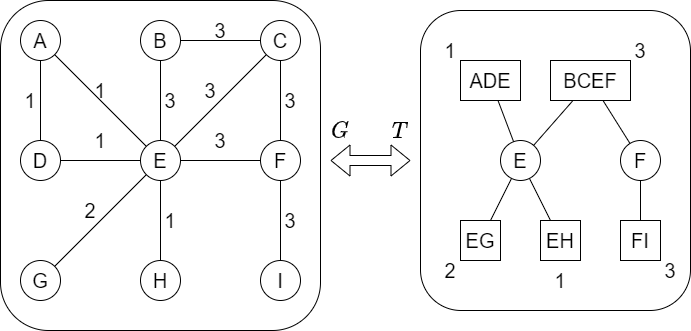
The following holds.
In a bad coloring of \(T\), there is a unique cut vertex \(v\) that is adjacent to a block in every color. Additionally, for each connected component of \(T\setminus \{v\}\), all blocks have the same color.
Let us show this fact. In a bad coloring, there is at least one vertex \(v\) that is adjacent to two or more colors. Let us take one such \(v\) and root \(T\) at \(v\). We may assume that \(v\) is adjacent to blocks in colors \(1\) and \(2\).
Then, a block in a subtree rooted at a block in color \(1\) adjacent to \(v\) will not have color \(3\). The same goes for a subtree rooted at a block in color \(2\). Thus, from the assumption that there is a block in every color, \(v\) is adjacent to a block in every color.

Then, it can be stated that a block in a subtree rooted at a block in color \(1\) does not have color \(2\) or \(3\), so all blocks there must have color \(1\). The same goes for blocks in colors \(2\) and \(3\). One can also easily verify that \(v\) is the only cut vertex that is adjacent to a block in every color.
Therefore, it can be seen that one can count bad colorings all of whose cycles are \(1\)-colored, as follows.
- For each cut vertex \(v\), let \(n_v\) be the number of blocks adjacent to \(v\).
- Then, there are \(\sum_{v} f(n_v)\) bad colorings all of whose cycles are \(1\)-colored, where \(f(n)\) is the number of surjections from an \(n\)-element set to \(\{1,2,3\}\).
posted:
last update: