F - Tri-Colored Paths 解説
by  maspy
maspy
ヒント → https://atcoder.jp/contests/arc153/editorial/5482
本解説において,グラフの二重連結成分や block-cut 木に関する基礎知識を仮定します.これらについては例えば次のサイトを参考にしてください.
次が成り立つ塗り方を悪い塗り方と呼ぶことにします.
- すべての色の辺が存在する.
- 問題の条件を満たさない.つまり,任意の単純パスは \(2\) 色以下の辺からなる.
本問は容易に悪い塗り方の数え上げに帰着できるので,以下ではその方法を解説します.
[1] 色数 \(3\) のサイクルについて
次を示します.
悪い塗り方において,\(C\) が色数 \(3\) のサイクルだとする.このとき次が成り立つ:
- \(C\) の長さは \(3\) である.
- \(N\geq 5\) のとき,\(C\) の頂点のうちで,\(C\) 外の頂点を隣接するものはちょうど \(1\) つである.
まず,\(C\) の長さが \(4\) 以上であるとすると,\(C\) からある \(1\) 辺を除いてできる単純パスがすべての色を含むので矛盾します.
\(C\) の長さが \(3\) であるとします.\(C\) の頂点が \(v_1, v_2, v_3\) とし,辺 \(v_1v_2\) の色が \(3\),辺 \(v_2v_3\) の色が \(1\),辺 \(v_3v_1\) の色が \(2\) であるとします.\(N\geq 5\) かつ \(v_1, v_2\) がともに \(C\) 外の頂点と隣接するとして矛盾を導きましょう.
\(v_1\) が隣接する \(C\) 外の頂点をひとつとり,\(x\) とします.\(v_2\) が隣接する \(C\) 外の頂点をひとつとり,\(y\) とします.
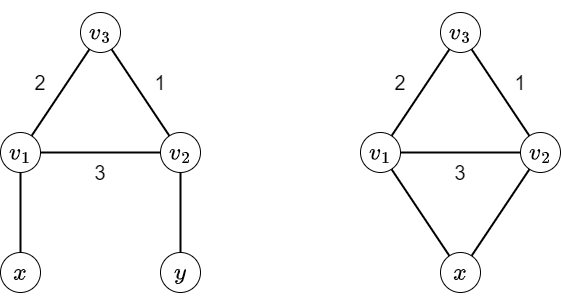
単純パス \((x,v_1,v_2,v_3)\) および \((x,v_1,v_3,v_2)\)から,辺 \(xv_1\) の色は \(1\) です.同様に辺 \(yv_2\) の色は \(2\) です.
\(x\neq y\) であるとき,単純パス \((x,v_1,v_2,y)\) がすべての色を含むため矛盾します.よって \(x = y\) です.
このとき,\(S = \{v_1,v_2,v_3,x\}\) とすれば,任意の \(s\in S\) および,\(2\) つの色 \(a, b\) に対して,\(s\) から始まる \(S\) 内の単純パスで色 \(a,b\) を含むものが存在します.\(N\geq 5 > |S|\) であるとき,ある \(s\in S\) の点と \(t\notin S\) を結ぶ辺が存在しますが,そのような辺と \(s\) から始まる \(S\) 内の単純パスを合わせることですべての色を含む単純パスが得られるので矛盾します.
以上の考察のもと,色数 \(3\) のサイクルが存在するような悪い塗り方を数え上げることが可能です.\(N\leq 4\) のときは,全ての塗り方や単純パスを調べることで解けるので,以下 \(N\geq 5\) であるとします.
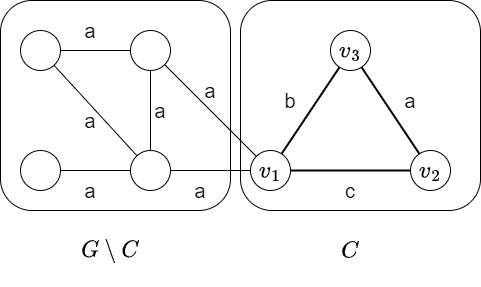
このような塗り方はあるサイクル \(C = (v_1,v_2,v_3)\) と異なる色 \(a, b, c\) について次を満たします.
- \(C\) は \(G\) の二重連結成分のひとつであり,\(C\) の点のうちで \(v_1\) のみが \(G\) の関節点である.
- \(v_1v_2\) の色は \(c\),\(v_2v_3\) の色は \(a\),\(v_3v_1\) の色は \(b\) である.
このとき \(C\) に含まれない任意の辺 \(e\) について,辺 \(e, v_1v_2, v_2v_3\) を含む単純パスが存在するので,\(e\) の色は \(b\) ではありません.同様に \(e\) の辺は \(c\) でもないので,\(e\) の色は \(a\) で確定します.
逆にそのような塗り方が必ず悪い塗り方であることや,色数 \(3\) のサイクルを唯一含むことも容易に確かめられます.したがって \(N\geq 5\) の場合,色数 \(3\) のサイクルを含む悪い塗り方は次のようにして数えられます:
- 長さ \(3\) のサイクル \(C\) であって,\(G\) の二重連結成分のひとつであり,\(G\) の関節点を唯一含むものの個数を \(n\) とする.
- 色数 \(3\) のサイクルを含む悪い塗り方は \(6n\) 通りである.
[2] 色数 \(2\) のサイクルについて
次を示します:
色数 \(3\) のサイクルを含まず,色数 \(2\) のサイクルを含むような,悪い塗り方は存在しない.
悪い塗り方をひとつとり,\(C\) が色 \(1\), 色 \(2\) を含み色 \(3\) を含まないサイクルであるとします.このとき,任意の \(x\in C\) について,\(x\) から始まり \(C\) 内の辺からなる単純パスで,色 \(1, 2\) をともに含むものが存在します.
どの辺 \(e\) の色も \(3\) ではないことを示しましょう.

\(e\) が \(C\) 外の点であるとします.\(e\) の色が \(3\) であるとすると,\(e\) を含み \(C\) に至るような単純パスをとり,\(C\) 内の単純パスと合わせることですべての色を含むパスが得られるので矛盾します.
\(e\) が \(C\) の弦(\(C\) の点同士を結ぶ,\(C\) に含まれない辺)だとします.\(e\) の色が \(3\) であるとします.\(e\) は \(C\) の辺を \(2\) つの部分 \(C_1, C_2\) に分割します.塗り方が色数 \(3\) のサイクルを含まないという仮定により,\(C_1\) の辺の色数は \(1\) です.同様に \(C_2\) の辺の色数も \(1\) です.このとき,\(e\) の前後に \(C_1, C_2\) の辺を追加した長さ \(3\) の単純パスの色数が \(3\) となり,悪い塗り方であることに矛盾します.
以上により任意の辺の色が \(3\) ではないことが示されましたが,これは,悪い塗り方の定義に反します.
[3] すべてのサイクルの色数が \(1\) である場合について
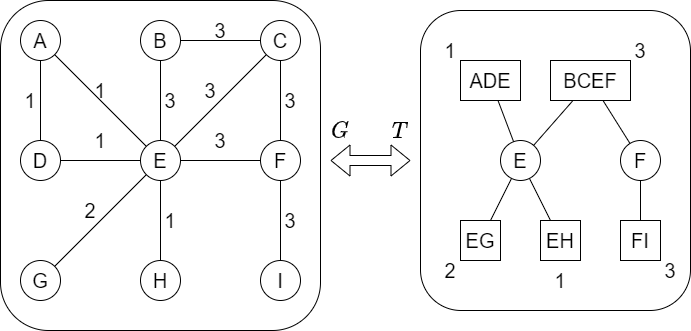
すべてのサイクルの色数が \(1\) であるような悪い塗り方について調べます.このような塗り方において,\(G\) の各二重連結成分における辺はすべて同色です.よって,block-cut 木に関する次の問題に帰着できます.
\(G\) の block-cut 木 \(T\) の各ブロックを色 \(1, 2, 3\) のいずれかで塗る方法であって,次を満たすものを数え上げよ.
- すべての色のブロックが存在する.
- \(T\) の単純パスであって,すべての色のブロックを含むものは存在しない.
このような塗り方を,「\(T\) の悪い塗り方」ということにします.
次が成り立ちます:
\(T\) の悪い塗り方において,すべての色のブロックに隣接するような関節点 \(v\) が唯一存在する.さらに \(T\setminus \{v\}\) の各連結成分について,全てのブロックは同色である.
このことを示しましょう.悪い塗り方において \(2\) 色以上の色に隣接するような頂点 \(v\) が少なくともひとつ存在します.そのような \(v\) をひとつとり,\(T\) を \(v\) を根とする根付き木として扱います.\(v\) が色 \(1, 2\) のブロックと隣接するとしてよいです.
このとき,\(v\) と隣接する色 \(1\) のブロックの部分木内のブロックの色は \(3\) にはなりません.色 \(2\) のブロックの部分木についても同様です.よって,すべての色のブロックが存在するという仮定より \(v\) はすべての色のブロックと隣接します.

すると色 \(1\) のブロックの部分木内のブロックの色は \(2\) でも \(3\) でもないことがいえるので,色 \(1\) のブロック内の色はすべて色 \(1\) であることが分かります.色 \(2\), \(3\) のブロックについても同様です.\(v\) がすべての色のブロックと隣接するような唯一の関節点であることも容易に確かめられます.
以上により,すべてのサイクルの色数が \(1\) である場合の悪い塗り方の数え上げは次のように行えることが分かります:
- 各関節点 \(v\) に対して,\(v\) が隣接するブロックの個数を \(n_v\) とする.
- すべてのサイクルの色数が \(1\) である場合の悪い塗り方は,\(\sum_{v} f(n_v)\) 個である.ただし \(f(n)\) は \(n\) 元集合から \(\{1,2,3\}\) への全射の個数である.
投稿日時:
最終更新: