Since the operation doubles the number of edges, the objective is obviously unachievable when \(N\) is even. When \(N\) is odd, it turns out that there is always a desired set of edges. Here is one way to construct one.

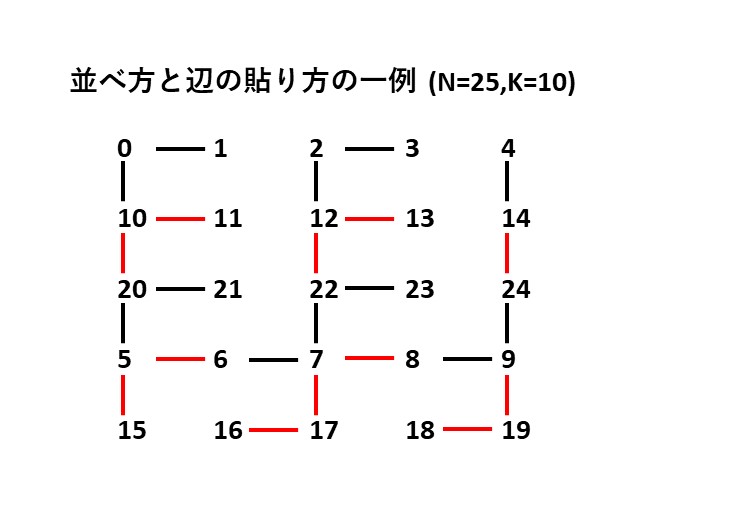
Let \(g\) be the greatest common divisor of \(N\) and \(K\), and \(n=N/g, k=K/g\). Let us classify \(0\) through \(N-1\) according to the remainder when divided by \(g\) to arrange them in \(n\) rows from top to bottom and \(g\) columns from left to right, where each column consists of the numbers with the same remainder. The numbers in the column with the remainder \(0\) are \(0,K\) \( \mathrm{mod}\) \(N, 2K\) \(\mathrm{mod}\) \( N,\ldots , (n-1)K\) \(\mathrm{mod}\) \( N\) from top to bottom. Since \(n\) and \(k\) are coprime, each number from \(0\) through \(n-1\) appear once in \(0, k\) \(\mathrm{mod}\) \(n, 2k\) \(\mathrm{mod}\) \(n,\ldots , (n-1)k\) \(\mathrm{mod}\), so if they are multiplied by \(g\), which results in the above sequence, each multiple of \(g\) appears once. In the columns with a remainder of \(1\) or greater, each number should be one greater than the number on the left, as shown in the figure below.

Then, each number from \(0\) through \(N-1\) appears once, and the numbers of rows and columns are odd. As shown in the figure (where \(N=25\) and \(K=10\)), if we draw vertical edges in the odd-numbered (\(1\)-st, \(3\)-rd, …) columns, \(n-1\) horizontal edges from the upper part of each odd-numbered column, and \(2\) horizontal edges from the lower part of each even-numbered column, we have a tree. Here, if we add the black edges in the figure ourselves, each will spawn the red edge right below it, satisfying the requirement.

(“並べ方と辺の貼り方の一例”: One way to arrange numbers and add edges)