操作によって辺の数が \(2\) 倍になるため、\(N\) が偶数の時は明らかに不可能です。 \(N\) が奇数であるとき、実は常に条件を満たすような辺の組が存在します。以下、構築方法の一例を記します。

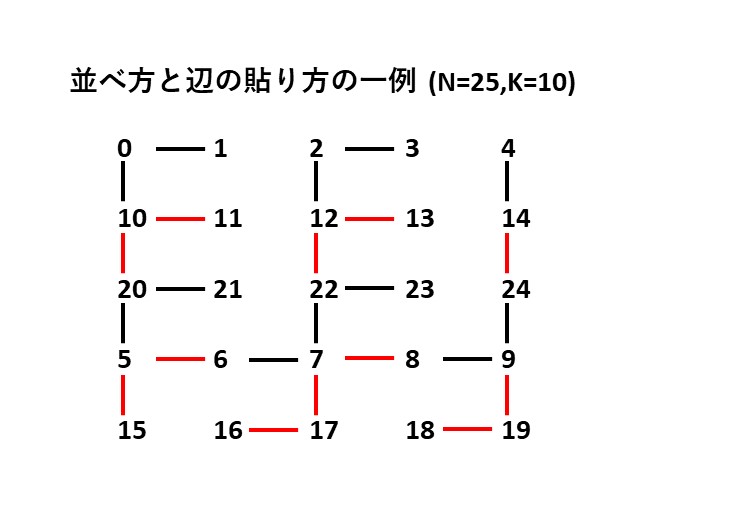
\(N\) と \(K\) の最大公約数を \(g\) とし、\(n=N/g, k=K/g\) とします。 このとき、\(g\) で割った余りで \(0～N-1\) を分類し、同じ余りのものを縦にして横幅 \(g\) 、縦幅 \(n\) に並べることを考えます。 余り \(0\) のものを縦に並べる際、上から順に \(0,K\) \( \mathrm{mod}\) \(N, 2K\) \(\mathrm{mod}\) \( N,\ldots , (n-1)K\) \(\mathrm{mod}\) \( N\) となるようにします。 \(n\) と \(k\) が互いに素であることから、\(0, k\) \(\mathrm{mod}\) \(n, 2k\) \(\mathrm{mod}\) \(n,\ldots , (n-1)k\) \(\mathrm{mod}\) \(n\) には \(0～n-1\) までが \(1\) 回ずつ現れるので、 これに \(g\) をかけた上記数列には \(g\) の倍数が全て \(1\) 回ずつ登場します。 余りが \(1\) 以上のものは、余り \(0\) の数の横に \(1\) ずつ加算して図のように並べます。

このとき、\(0～N-1\) までの数が \(1\) 回ずつ登場し、また縦横の個数は奇数です。 図（\(N=25, K=10\) の例）のように、奇数列目には縦線を、奇数列目から右には上から \(n-1\) 個の横線を、偶数列目から右には下から \(2\) 個の横線を結ぶと、 このグラフは木をなし、また図中の黒い線を元の辺とすれば、それぞれ直下の赤い線が操作で生じることとなるので、題意を満たす辺の組となります。