Hints → https://atcoder.jp/contests/arc149/editorial/4961

---

[1] Basic policy

For positive integers \(1\leq d\leq 9\) and \(n\), let \(x(n, d)\) denote the integer made by concatenating \(n\) copies of \(d\):

\[x(n, d) = \underbrace{dd\cdots dd}_{n}\]

.

The problem asks us to find the maximum integer that can be written as \(x(n, d)\) (\(1\leq n\leq N\), \(1\leq d\leq 9\)) and is a multiple of \(M\). Since there are \(9N\) numbers \(x(n, d)\) in total, even if we do a computation taking \(O(1)\) time for every \(x(n,d)\), it takes \(O(N)\) time in total. It leads us to think of the following solution.

• Compute \(x(n, d) \bmod M\) for every \((n, d)\).
• Find the maximum \(x(n,d)\) such that \(x(n, d) \bmod M = 0\).

The second part, finding the maximum, is simple: we just choose the one with the maximum \(d\) among the ones with the maximum \(n\). Below, let us explain how to compute \(x(n, d) \bmod M\) for every \((n, d)\).

---

[2] Computing \(x(n,d) \bmod M\)

Here are two ways to compute \(x(n,d)\bmod M\) assuming that \(x(n-1,d) \bmod M\), etc. are already known, allowing us to find all the desired \(x(n,d)\bmod M\) in \(O(N)\) time.

---

[2 - 1] Computing \(x(n,d)\) (1)

By noting that \(x(n-1, d)\) is a prefix of \(x(n,d)\), we see that:

\[x(n,d) = 10x(n-1,d) + d\]

.

One can compute each \(x(n,d)\bmod M\) in \(O(1)\) time by using this formula to do the computation in ascending order of \(n\).

---

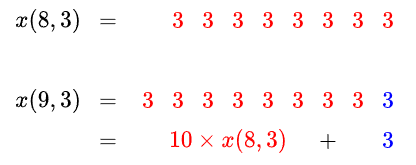
[2 - 2] Computing \(x(n,d)\) (2)

By noting that \(x(n-1, d)\) is a suffix of \(x(n,d)\), we see that:

\[x(n,d) = d\times 10^{n-1} + x(n-1,d).\]

If one uses this formula, one also needs the values \(10^{n-1}\bmod M\), which can also be computed in ascending order of \(n\) using \(10^n = 10\times 10^{n-1}\), allowing one to compute each \(x(n,d)\bmod M\) in \(O(1)\) time again.

---

[3] Advanced topics

One can also find the \((n,d)\) giving the maximum faster, as follows.

• Fix \(d\).
• Find the smallest positive integer \(n\) such that \(x(n,d)\) is a multiple of \(M\), which can be done similarly to Problem G in ABC 270 by noting \(x(n,d) = 10x(n-1,d) + d\).
• Let \(n_0\) be the smallest positive integer \(n\) such that \(x(n,d)\) is a multiple of \(M\). Then, one can prove that \(x(n,d)\) is a multiple of \(M\) if and only if \(n\) is a multiple of \(n_0\). Thus, one can find the largest \(n\) by finding the largest multiple of \(n_0\) at most \(N\), which can be done in \(O(1)\) time.

This method allows one to find the optimal \((n,d)\) in an expected time complexity of \(O(\sqrt{N})\) etc. One can find it even faster by using fast prime factorization, \(x(n,d) = d\cdot \frac{10^n-1}{9}\), and Euler’s theorem, etc.

In this problem, however, it takes \(\Omega(N)\) time to print the answer, so these methods do not allow one to solve it in \(o(N)\) time.

---

Sample submission

https://atcoder.jp/contests/arc149/submissions/35220937