ヒント → https://atcoder.jp/contests/arc149/editorial/4868

[1] 偶奇性の利用

\(4\) 以上の偶数は素数ではないことを利用します． 具体的には，マス目の上半分に奇数，下半分に偶数を書き込むことにしましょう．相異なる正の奇数同士・正の偶数同士の和は \(4\) 以上の偶数なので，素数になりません．したがって，このような書き込み方について，大部分の隣接する \(2\) 数の和の大部分が素数にならないことが確定します．

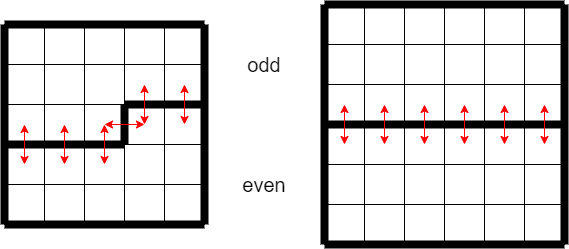
あとは，奇数と偶数が隣接する部分が素数でなくなる方法を考えればよいです．

[2] \(3\) の倍数の利用

[1] の書き込み方のもと，あとは \(1\) 以上 \(N^2\) 以下の奇数・偶数の組で，和が素数ではないものを \(N\) 組程度作り，それらを偶奇の境界部分に配置すれば目標を達成することができます．

これはかなり緩い条件なので達成する方法は多く考えられますが，ここではさらに，和が \(6\) 以上の \(3\) の倍数になるようにすることで目標を達成する方法を紹介します．

\(N\geq 6\) のとき，\(3\) の倍数であるような奇数・偶数が \(N\) 個以上存在します．これらを境界に並べるようにすればよいです．

簡潔な実装方法としては，例えばマス目の上から順に

• \(3\) の倍数ではない奇数
• \(3\) の倍数である奇数
• \(3\) の倍数である偶数
• \(3\) の倍数ではない偶数

のうち未使用のものを書きこんでいくという方法が考えられます．

すべての境界部分に \(3\) の倍数を書き込むという方針では \(3\leq N\leq 5\) の場合を解くことはできません．解けていないものはその \(3\) 通りだけなので，その程度であれば手計算したものをソースコードに埋め込んでしまってもよいでしょう．例えば次のようにすればよいです．

なお，\(N=4\) については問題の出力例を利用することもできます．

解答例

https://atcoder.jp/contests/arc149/submissions/35220957