A - Repdigit Number Editorial
by  maspy
maspy
ヒント → https://atcoder.jp/contests/arc149/editorial/4868
[1] 基本方針
正整数 \(1\leq d\leq 9\) および \(n\) に対して,\(d\) を \(n\) 個並べてできる整数を \(x(n, d)\) と書くことにします:
\[x(n, d) = \underbrace{dd\cdots dd}_{n}\]
本問題は,\(x(n, d)\) (\(1\leq n\leq N\), \(1\leq d\leq 9\)) と書ける整数のうち \(M\) の倍数であるものの最大値を求める問題です.\(x(n, d)\) は全部で \(9N\) 個しかないので,すべての \(x(n,d)\) に対して \(O(1)\) 時間の計算を行っても全体の時間計算量は \(O(N)\) になります.したがって,次のような解法が考えられそうです.
- すべての \((n, d)\) に対して \(x(n, d) \bmod M\) を計算する.
- \(x(n, d) \bmod M = 0\) であるような \(x(n,d)\) のうちで最大のものを求める.
このうち「最大のもの」の計算は簡単で,\(n\) が最大のもののうちで \(d\) が最大のものを選べばよいです.以下では,すべての \((n, d)\) に対して \(x(n, d) \bmod M\) を計算する方法を解説します.
[2] \(x(n,d) \bmod M\) の計算
\(x(n-1,d) \bmod M\) などを既知として、\(x(n,d)\bmod M\) を計算する方法を,\(2\) つ紹介します.これらの方法によって,求めるべき \(x(n,d)\bmod M\) 全体を合計 \(O(N)\) 時間で計算できます.
[2 - 1] \(x(n,d)\) の計算方法 (1)
\(x(n-1, d)\) が \(x(n,d)\) の接頭辞であることに注目すると,
\[x(n,d) = 10x(n-1,d) + d\]
が成り立つことが分かります.この式を用いて小さな \(n\) から順に計算することで,各 \(x(n,d)\bmod M\) がひとつあたり \(O(1)\) 時間で計算できます.
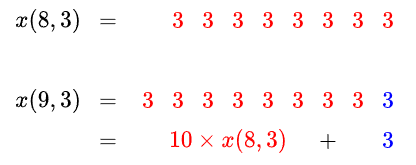
[2 - 2] \(x(n,d)\) の計算方法 (2)
\(x(n-1, d)\) が \(x(n,d)\) の接尾辞であることに注目すると,
\[x(n,d) = d\times 10^{n-1} + x(n-1,d)\]
が成り立つことが分かります.この式を用いる場合には \(10^{n-1}\bmod M\) の値が必要になりますが,この値も \(10^n = 10\times 10^{n-1}\) を用いて小さな \(n\) から順に計算していくと,各 \(x(n,d)\bmod M\) がひとつあたり \(O(1)\) 時間で計算できます.

[3] 発展
次のような手順によって,最大値を与える \((n,d)\) をより高速な計算量で求めることもできます.
- \(d\) を固定して考える.
- \(x(n,d)\) が \(M\) の倍数となる最小の正整数 \(n\) を求める.これは,\(x(n,d) = 10x(n-1,d) + d\) に注目すると ABC 270 問題G と同様に解ける.
- \(x(n,d)\) が \(M\) の倍数となる最小の正整数 \(n\) を \(n_0\) とするとき,「\(x(n,d)\) が \(M\) の倍数である」ことと「\(n\) が \(n_0\) の倍数である」ことが同値であることが証明できる.したがって,最大の \(n\) を求めるには \(N\) 以下の最大の \(n_0\) の倍数を求めればよく,これは \(O(1)\) 時間でできる.
この方法によって期待計算時間 \(O(\sqrt{N})\) などで最適な \((n,d)\) を求めることができます.また,高速な素因数分解と \(x(n,d) = d\cdot \frac{10^n-1}{9}\),Euler の定理などを用いてより高速に最適な \((n,d)\) を求めることも可能です.
ただし,本問では答の出力に \(\Omega(N)\) 時間かかるため,これらの解法でも \(o(N)\) 時間で解けるというわけではありません.
解答例
posted:
last update: