By dividing values such as \(a\), \(m\), and \(A_i\) by \(\gcd(a,m)\), the problem can be reduced to the case \(\gcd(a,m)=1\). Below, we assume \(\gcd(a,m)=1\).

---

[1] Remodeling with Grundy numbers

Let us define a function \(G\colon \{0, 1, 2, \ldots \} \longrightarrow \{0, 1, 2, \ldots \}\) recursively by:

• \(G(n) = \mathrm{mex}\{G(n-x)\mid x \in X, x\leq n\}\).

This is the Grundy number of the game where the sequence has only one term \(n\). The problem can then be rephrased into the following:

Find the number of pairs \((i,x)\) of an index \(i\) and \(x\in X\) such that \(G(A_1)\oplus \cdots \oplus G(A_n) = G(A_i) \oplus G(A_i - x)\).

Thus, the problem will be solved if one can:

• compute \(G(n)\) for a given \(n\);
• count \(x\in X\) such that \(G(n-x)=g\) for a given \(n\) and \(g\).

---

[2] The case \(a=0\)

It follows from \(\gcd(a,m)=1\) that \(m=1\), so we have \(X = \{1,2,3,4,\ldots\}\). This is exactly the game called Nim, so it is easy to find that \(G(n) = n\).

---

[3] Representing states with a grid

Below, we assume \(a > 0\). Consider a grid with infinite numbers of rows and columns labeled with integers, and let the square at Row \(x\) and Column \(y\) correspond to the number \(mx+ay\).

For instance, when \(m=10\) and \(a=3\), the squares corresponding to non-negative integers are arranged as shown in the following figure:

Since \(\gcd(a,m)=1\), all non-negative integers appear in this grid. Instead of a number, let us use one of the corresponding squares. Then, we are to study the Grundy numbers of the squares in the game where the players make the following move in each turn:

• move one square left and zero or more squares up.

---

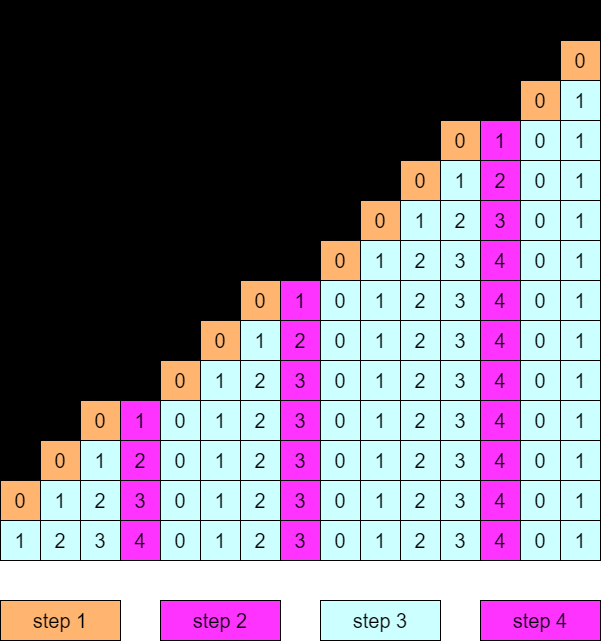
[4 - 1] The case \(0 < a \leq m/2\)

The Grundy numbers of the squares can be determined as follows:

Step 1

The Grundy number of a square whose left neighbor is a negative integer is \(0\).

Step 2

Look at a column on the (immediate) right of a column containing a square confirmed as \(0\) in Step 1. Let us call such a column special. The Grundy numbers of the squares in a special column are still difficult to find, but they are confirmed to be at least \(1\).

Step 3

The Grundy numbers of the squares in the column on the right of a special column must be \(0\). In the column on the right of that column, the Grundy numbers of all squares must be \(1\). In the next column on the right, the Grundy numbers of all squares must be \(0\). In this manner, one can determine the Grundy numbers in the columns until reaching another special column.

Step 4

At this point, the Grundy numbers of all squares except the special columns are already confirmed. Since \(a\leq m/2\), there are no two consecutive special columns. Therefore, in the column on the left of a special column, all Grundy numbers are confirmed, so we can also determine the Grundy numbers in the special column.

---

[4 - 2] The case \(m/2 < a < m\)

Let us call a square immediately below a negative integer a top square. Since \(m/2 < a\), there can be at most two horizontally consecutive top squares. Additionally, since \(a < m\), there do exist two horizontally consecutive top squares.

Now, the Grundy numbers of the squares can be determined as follows:

Step 1

The Grundy number of a square whose left neighbor is a negative integer is \(0\).

Step 2

For each pair of horizontally consecutive top squares, let us call the column containing the right top square special. The Grundy numbers of the squares in a special column are still difficult to find, but they are confirmed to be at least \(1\).

Step 3

The Grundy numbers of the squares in the column on the right of a special column must be \(0\). If we proceed to the right, the top square keeps moving up one square until we reach another special column. Thus, the sequence of the Grundy numbers in a column transitions as follows:

\[(0,0,0,0,0,0,\ldots)\to (0,1,1,1,1,1,\ldots)\to(0,1,2,2,2,2\ldots)\to (0,1,2,3,3,3,\ldots).\]

Step 4

At this point, the Grundy numbers of all squares except the special columns are already confirmed. In the column on the left of a special column, the sequence of Grundy numbers looks like \((0,1,2,3,3,3\ldots)\), so one can see that it also looks like \((1,2,3,4,4,4,\ldots)\) in the special column.

---

[5] Summary

[2], [4-1], and [4-2] have revealed the patterns of the Grundy numbers in all possible cases. It is not difficult to use these to:

• compute \(G(n)\) for a given \(n\);
• count \(x\in X\) such that \(G(n-x)=g\) for a given \(n\) and \(g\).

One can also compute the relative position of the top and “leftmost” squares and such from a certain square using the remainder of division by \(m\) and \(a\).

Each of these computations can be done in \(O(1)\) time, so the problem can be solved in \(O(N)\) time.