[1] Conversion to edge weight

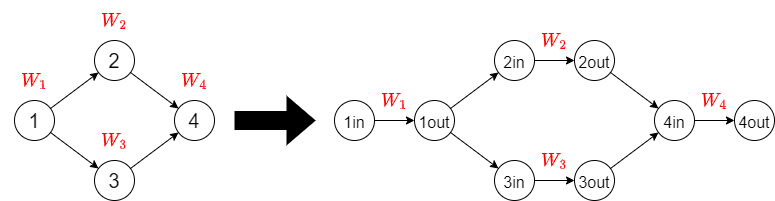
The problem considers the total vertex weight of a path. It is occasionally easier to handle total edge weight than total vertex weight (because, for example, it acts additively with respect to the concatenation of paths), so let us first convert our subject of study to total vertex weight by building a graph \(G'\) as follows:

• For each vertex \(v\) in \(G\), make two vertices \(v_{\text{in}}, v_{\text{out}}\), for a total of \(2N\), which will be the vertices in \(G'\).
• For each directed edge \(vw\) in \(G\), span a directed edge \(v_{\text{out}}w_{\text{in}}\) with a weight of \(0\) in \(G'\).
• If a vertex \(v\) in \(G\) has a weight of \(W_v\), span a directed edge \(v_{\text{in}}v_{\text{out}}\) with a weight of \(W_v\) in \(G'\).

The problem is now reduced to the following:

You are given a DAG with weighted edges, a source \(s\), and a sink \(t\). Some edges have weights of -1, which means “undecided”. Maximize the \(\gcd\) of total edge weights of all \(st\)-paths by appropriately setting the undecided edge weights.

Below, the total edge weight of a path is simply called the weight of the path.

---

[2] Rephrasing the decision problem

First, for a fixed \(x\), consider the decision problem to determine whether one can make the weights of all \(st\)-paths divisible by \(x\).

Obviously, one does not need to consider the following vertices:

• the vertices unreachable from \(s\);
• the vertices from which \(t\) is unreachable.

By deleting those vertices beforehand, we can assume that for all \(v\), both \(sv\)- and \(vt\)-paths exist.

Under this assumption, one can make the weights of all \(st\)-paths divisible by \(x\) if and only if:

one can assign to each vertex \(v\) an integer value \(P_v\) called potential to satisfy the following:

• \(P_s \equiv P_t\pmod{x}\);
• \(P_w \equiv P_v + c\pmod{x}\), if a directed edge \(vw\) has a fixed weight of \(c\).

---

We will prove the necessity first. Assume that one was able to make the weights of all \(st\)-paths divisible by \(x\). Let \(P_v\) be the weight of some \(sv\)-path (remember the assumption that a \(sv\)-path exists). We have \(P_s = 0\), and from the fact that all \(st\)-paths have weights divisible by \(x\), we also have \(P_t\equiv 0\pmod{x}\), so \(P_s \equiv P_t\pmod{x}\) holds.

Let us show that \(P_w \equiv P_v + c\pmod{x}\) when a directed edge \(vw\) has a weight of \(c\). Combining this edge and an \(sv\)-path with a weight of \(P_v\), there is an \(sw\)-path with a weight of \(P_v+c\). There is also an \(sw\)-path with a weight of \(P_w\). Additionally, take an \(wt\)-path whose existence is guaranteed by the assumption, and let \(d\) be its weight. Then, we obtain an \(st\)-path with a weight of \(P_v+c+d\) and an \(st\)-path with a weight of \(P_w + d\). It follows from both \(P_v + c + d\) and \(P_w + d\) being divisible by \(x\) that \(P_w \equiv P_v + c\pmod{x}\).

---

Next, we will prove the sufficiency. Assume that one was able to assign the potentials \(P_v\) to satisfy the conditions. For each directed edge \(vw\) with an undecided weight, we set its weight \(c\) in some way such that \(P_v + c \equiv P_w\pmod{x}\).

Then, it can be verified that the weight of every \(uv\)-path is congruent to \(P_v - P_u\) \(\pmod{x}\) by induction on the length of a path. Particularly, the weight of every \(st\)-path is congruent to \(P_t - P_s\) \(\pmod{x}\), which, combined with \(P_s \equiv P_t\pmod{x}\), shows that the weight of every \(st\)-path is divisible by \(x\).

---

[3] The solution to the original problem

The decision problem to determine whether one can make the weights of all \(st\)-paths divisible by \(x\), has been reduced to the following problem:

You are given some pieces of information in the form \(P_v \equiv P_w + c \pmod{x}\). Determine whether one can set a sequence of potentials \((P_v)_v\) without contradicting them.

This can be solved by managing the information network by maintaining the connected component that each vertex belongs to, the potentials of the representatives, and the differences in potential between vertices. For more information, try searching the web for weighted union-find.

Alternatively, since there is no need to add information dynamically, one can also perform DFS on each connected component to set the potential for each vertex.

---

The original problem asks the maximum \(x\) such that the answer for the decision problem is yes, but the solution for this case is almost the same. Solving the decision problem involves determining whether a certain value is divisible by \(x\) some finite number of times. This time, we should find the maximum \(x\) that passes all those checks, which can be computed as the greatest common divisor of some values.

Therefore, the problem can be solved in \(O(N+M + \log \sum A_i)\) time or similar.