[1] 辺重みへの変換

本問ではパスの頂点重みの和が考察対象となっています． 頂点重みの和よりも辺重みの和の方が扱いやすいことがある（例えばパスの結合に対して加法的に振る舞うため）ので，まず次のようにしてグラフ \(G'\) を作ることで，考察対象をパスの辺重みの和に変換します．

• 各 \(G\) の頂点 \(v\) に対して，\(2\) つの頂点 \(v_{\text{in}}, v_{\text{out}}\) を作り，それら合計 \(2N\) 個の頂点を \(G'\) の頂点とする．
• \(G\) に有向辺 \(vw\) があるとき，\(G'\) に重み \(0\) の有向辺 \(v_{\text{out}}w_{\text{in}}\) をはる．
• \(G\) の頂点 \(v\) の重みが \(W_v\) であるとき，\(G'\) に重み \(W_v\) の有向辺 \(v_{\text{in}}v_{\text{out}}\) をはる．

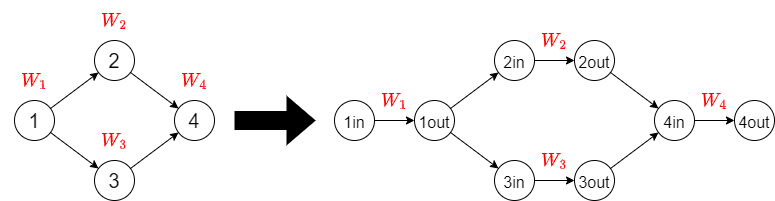
本問題は次の問題に帰着できました．

辺が重みを持つ DAG と始点 \(s\)，終点 \(t\) が与えられる．ただし辺重みの一部は -1 となっており未定である．未定の辺重みを上手く定めることで，すべての \(st\) パスの辺重みの和の \(\gcd\) を最大化せよ．

以下ではパスの辺重みの和を単にパスの重みということにします．

---

[2] 判定問題の言い換え

まずは，\(x\) を固定したときに，「すべての \(st\) パスの重みを \(x\) の倍数にできるか」を判定する判定問題を考えます．

まずこの問題において明らかに，

• \(s\) から到達不可能であるような頂点
• \(t\) へ到達不可能であるような頂点

は考える必要がありません．そのような頂点は予め削除することで，任意の \(v\) に対して \(sv\) パス・\(vt\) パスの両方が存在するとしてよいです．

上記の仮定のもとで，すべての \(st\) パスの辺重みの和の \(x\) の倍数にできるという判定問題は，次と同値です：

各頂点 \(v\) にポテンシャルという整数値 \(P_v\) を割り当てることで，次が成り立つようにできる：

• \(P_s \equiv P_t\pmod{x}\)
• 有向辺 \(vw\) が重み \(c\) を持つことが確定しているとき，\(P_w \equiv P_v + c\pmod{x}\) が成り立つ．

---

まず必要性を証明します． 任意の \(st\) パスの重みが \(x\) の倍数となるようにできたとします．\(P_v\) を適当な \(sv\) パスの重みとして定めます（\(sv\) パスが存在するという仮定に注意）．\(P_s = 0\) であり，任意の \(st\) パスの重みが \(x\) の倍数であることより \(P_t\equiv 0\pmod{x}\) であるので，\(P_s \equiv P_t\pmod{x}\) が成り立ちます．

有向辺 \(vw\) が重み \(c\) を持つときに \(P_w \equiv P_v + c\pmod{x}\) を示します．重み \(P_v\) の \(sv\) パスとこの有向辺を合わせて重み \(P_v+c\) の \(sw\) パスが存在することになります．重み \(P_w\) の \(sw\) パスも存在します． また仮定より \(wt\) パスが存在するのでそれをひとつとり，その重みを \(d\) とすれば，重み \(P_v+c+d\) の \(st\) パスおよび 重み \(P_w + d\) の \(st\) パスが得られます．\(P_v + c + d\) および \(P_w + d\) がどちらも \(x\) の倍数であることから \(P_w \equiv P_v + c\pmod{x}\) が分かります．

---

次に十分性を示します．条件を満たすようにポテンシャル \(P_v\) を定められたとします．辺重みが未定であるような有向辺 \(vw\) の重み \(c\) を，\(P_v + c \equiv P_w\pmod{x}\) が成り立つように適当に定めます．

このとき，任意の \(uv\) パスの重みが \(\mod{x}\) で \(P_v - P_u\) に等しいことが，パスの長さに関する帰納法により確かめられます．特に任意の \(st\) パスの重みが \(\mod{x}\) で \(P_t - P_s\) に等しいことが分かり，\(P_s \equiv P_t\pmod{x}\) と合わせて任意の \(st\) パスの重みが \(x\) の倍数であることが示されます。

---

[3] 本問題の解法

まず，全ての \(st\) パスの重みを \(x\) の倍数にできるかという判定問題は，次の問題に帰着できるのでした．

\(P_v \equiv P_w + c \pmod{x}\) という情報がいくつか与えられる．これらに矛盾しないようにポテンシャルの列 \((P_v)_v\) を定められるか否かを判定せよ．

これは，情報関係に対する各頂点の連結成分および，その代表点のポテンシャルと各頂点のポテンシャルの差分を管理することで行えます．詳しくは重み付き UnionFind，ポテンシャル付き UnionFindなどの単語で検索してください．

また，情報の追加を動的に行う必要がないので，連結成分ごとにグラフを dfs しながら各頂点のポテンシャルを決めていくという方法でも判定を行うことができます．

---

本問題では，判定問題が肯定的であるような \(x\) の最大値が問われていますが，この場合の解法もほとんど同じです．上の判定問題を解く際には「ある値が \(x\) の倍数であるか？」を有限回判定することになります．これらがすべて真となるような \(x\) の最大値を答えればよいので，いくつかの値の最大公約数をとる形で答が計算できます．

したがって本問題は \(O(N+M + \log \sum A_i)\) などの計算量で解くことができます．